【图像加密】基于双随机相位编码实现图像加密解密含Matlab源码

1 简介

21世纪以来,互联网和数字通讯技术的普及和快速发展给人们的工作和生活提供了极大的便利。但与此同时,如何确保网络信息的安全也成为了一个不能被忽视的课题。数字图像作为互联网中最常见的一种信息表达方式,其安全问题也得到了人们的广泛关注,而图像加密技术是保障图像安全性能的一项关键技术。光学图像加密技术,跟过去的计算机图像加密技术相比,具有容量大、加密速度快、可多路并行传输、多密匙维度等与生俱来的优势,这些优势都使得应用光学的方法进行图像加密更加快捷高效。虽然当今国内外关于光学信息安全领域的研究已获得了显著的进展,但依然还处于探索和实验阶段,仍然需要进行更加系统而深入的研究。本论文通过理论分析结合计算机仿真模拟,对基于双随机相位编码(DRPE)的光学图像加密算法进行了系统的研究,对几种典型的光学图像加密系统进行了深入的分析,并对能同时增强系统安全性和鲁棒性的加密方案进行了探讨。本文的主要内容包括下面的4个方面:1、概述了传统密码学的相关概念和重要理论,介绍了与光学图像加密相关的基础理论知识,以便大家从整体上掌握光学图像加密的基本内容,为后面研究光学图像加密系统奠定好理论基础。2、深入分析了四种典型的光学加密系统:基于傅立叶变换的DRPE系统、基于菲涅尔衍射的DRPE系统、基于干涉原理的光学加密系统及基于相位截断傅立叶变换(PTFT)的非对称光学加密系统。详细剖析了每种系统的加密和解密算法,并通过MATLAB仿真软件各有侧重地对每种系统的可行性和安全性进行了仿真模拟。同时对仿真结果展开了详尽的分析,并针对系统存在的不足给出了相应的改进分析。3、针对基于PTFT的非对称光学加密系统容易遭受基于迭代的振幅相位恢复(APR)算法的特殊攻击这一问题,设计了一种基于相位截断菲涅尔衍射(PTFD)的非线性图像加密系统。该系统利用一个随机振幅板(RAM)和两个公匙产生两个私匙用于系统的加密。系统的非线性使其可以抵御选择密文攻击(CCA)、选择明文攻击(CPA)及已知明文攻击(KPA),同时由于缺乏限制条件,攻击者想要用迭代的APR算法来破译该系统是行不通的。我们对系统的加密和解密算法进行了理论分析,并通过计算机仿真对该算法的可行性和安全性进行了验证。4、将纠错能力较强的快速响应(QR)码引入到了所设计的加密系统中,使系统的鲁棒性得以增强。待加密图像首先被转换成QR码,然后经过基于PTFD的加密系统进行加密。解密时得到含噪声的QR码,用智能手机或者平板电脑里面的扫码软件扫描该QR码即可得到无噪声的原始图像。仿真结果也表明即使密文受到噪声的干扰或者其部分信息丢失,我们仍然能够无失真地恢复初始明文图像。

2 部分代码

function makeEnterKey(hObject, eventdata, handles)global ArnoldCount LogisticX LogisticU LogisticN ChenX ChenY ChenZ ChenC ChenH ChenT ChenN;% % SZ=get(0,'ScreenSize');% % h=figure('menubar','none','position',[SZ(3)/5,SZ(4)/5,600,400],'units','normalized');% % str='adfasdf';% % hText=uicontrol(h,'style','edit','string',str,'fontsize',10,'position',[100 350 70 60]);% % ​prompt = {'ArnoldCount(>=0):','LogisticX():','LogisticU():','LogisticN():','ChenX():','ChenY():','ChenZ():','ChenC():','ChenH():','ChenT():','ChenN():'};dlg_title = 'Input';num_lines = 1;defaultans = {num2str(ArnoldCount),num2str(LogisticX),num2str(LogisticU),num2str(LogisticN), num2str(ChenX),num2str(ChenY),num2str(ChenZ),num2str(ChenC),num2str(ChenH),num2str(ChenT),num2str(ChenN)};% defaultans = {num2str(ArnoldCount),LogisticX,LogisticU,LogisticN, ChenX,ChenY,ChenZ,ChenC,ChenH,ChenT,ChenN};% defaultans = {'8', '0.5','3.9','500', '2','1','3','28','0.001','0','2000'};k= inputdlg(prompt,dlg_title,num_lines,defaultans);if isempty(k)    return;endkey(11)=0;for i=1:11    key(i)=str2num(k{i});endArnoldCount=key(1);LogisticX=key(2);LogisticU=key(3);LogisticN=key(4);ChenX=key(5);ChenY=key(6);ChenZ=key(7);ChenC=key(8);ChenH=key(9);ChenT=key(10);ChenN=key(11);setappdata(handles.figure,'KeyFlag',true);

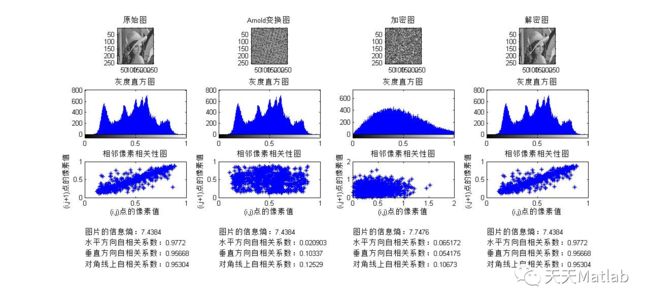
3 仿真结果

4 参考文献

[1]宋利. 基于双随机相位编码的光学图像加密方法研究. Diss. 电子科技大学, 2016.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。