【机器学习】谱聚类(Spectral Clustering)
疑问
谱聚类的概念
谱聚类是一种针对图结构的聚类方法,将每个点都看作是一个图结构上的点,所以,判断两个点是否属于同一类的依据就是,两个点在图结构上是否有边相连,可以是直接相连也可以是间接相连。本质上就是一个图切割问题。
什么是谱(Spectral )
谱(spectral)就是指矩阵的特征值
那么谱与图的联系究竟是什么
首先我们知道 图结构 可以用邻接矩阵 / 相似矩阵来表示,通过矩阵就能清楚图的结构信息,具体是怎么建立联系的,我们接下来一步一步分析。
一、问题描述
假设有 n n n个实数样本数据如下,每个样本有 d d d维,目标是要聚 c c c个类,并且数据分布并非云团。
X = { x 1 d , x 2 d , … , x n d } T , X ∈ R n × d X=\left\{x_{1}^{d}, x_{2}^{d}, \ldots, x_{n}^{d}\right\}^{T}, \quad X \in R^{n \times d} X={x1d,x2d,…,xnd}T,X∈Rn×d
二、构造图结构
在图论中我们常用邻接矩阵W表示图(无向图是为了保证邻接矩阵是对称矩阵),因此我们只需按某个准则来计算数据点对之间的距离即可获得数据点的邻接矩阵。
W = [ w 11 w 12 w 13 w 21 w 22 w 23 w 31 w 32 w 33 ] W=\left[\begin{array}{lll} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \end{array}\right] W=⎣⎡w11w21w31w12w22w32w13w23w33⎦⎤
接下来主要介绍常用的,效果比较好的k-近邻图构造准则
k-近邻法
构造图的 相似矩阵(邻接矩阵)步骤:
1.计算点对之间的欧氏距离;
2.通过给定参数 k k k,选取距离当前点最近的k kk个点为邻居(常用高斯核计算距离),令其余点到该点距离为0。
w i j = { e − ∥ x i − x j ∥ 2 2 2 σ 2 if x i ∈ k n n ( x j ) 0 otherwise ( 可能存在 w i j ≠ w j i ) w_{i j}=\left\{\begin{array}{ll} e^{-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{2 \sigma^{2}}} & \text { if } x_{i} \in k n n\left(x_{j}\right) \\ 0 & \text { otherwise } \end{array} \quad\left(\text { 可能存在 } w_{i j} \neq w_{j i}\right)\right. wij={e−2σ2∥xi−xj∥220 if xi∈knn(xj) otherwise ( 可能存在 wij=wji)
这样构造的问题: 数据从有向图变成了无向图,即你是我的 k k k近邻,但我不一定属于你的 k k k近邻。为了保证相似矩阵的对称性
,论文[1] (A tutorial on spectral clustering) 给出两种解决方法;
方法1》 若两点间有两条有向边,则忽略一条仅保留一条,具体做法如下:
w i j = w j i = { e − ∥ x i − x j ∥ 2 2 2 σ 2 if x i ∈ knn ( x j ) or x j ∈ knn ( x i ) 0 otherwise w_{i j}=w_{j i}= \begin{cases}e^{-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{2 \sigma^{2}}} & \text { if } x_{i} \in \operatorname{knn}\left(x_{j}\right) \text { or } x_{j} \in \operatorname{knn}\left(x_{i}\right) \\ 0 & \text { otherwise }\end{cases} wij=wji=⎩⎨⎧e−2σ2∥xi−xj∥220 if xi∈knn(xj) or xj∈knn(xi) otherwise
方法2》当且仅当你是我的 k k k近邻,我也属于你的 k k k近邻时,这两点之间的边才有权值,具体做法如下:
w i j = w j i = { e − ∥ x i − x j ∥ 2 2 2 σ 2 if x i ∈ k n n ( x j ) and x j ∈ k n n ( x i ) 0 otherwise w_{i j}=w_{j i}= \begin{cases}e^{-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{2 \sigma^{2}}} & \text { if } x_{i} \in k n n\left(x_{j}\right) \text { and } x_{j} \in k n n\left(x_{i}\right) \\ 0 & \text { otherwise }\end{cases} wij=wji=⎩⎨⎧e−2σ2∥xi−xj∥220 if xi∈knn(xj) and xj∈knn(xi) otherwise
而实战中常采用的方法则是:
W = W + W T 2 W=\frac{W+W^{T}}{2} W=2W+WT
简单粗暴!
三、确定目标函数
构造好了图结构,将数据点聚成 c c c个类的问题,可以转换将无向图 切割为 c c c个子图的问题。
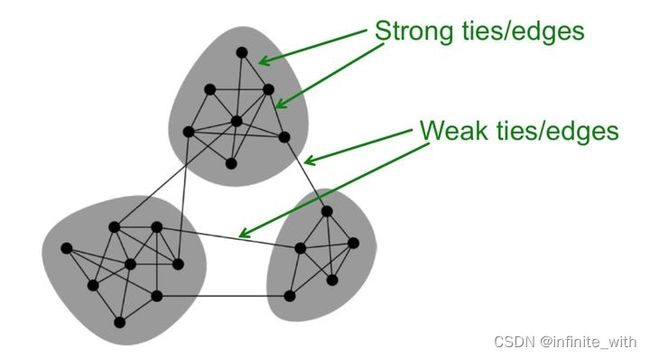
由上图可知,很容易想到一个准则,即我们将距离较远(相似度较低)的两个点切分到不同子图时,需要付出代价最小。因此我们可以定义一个代价函数来作为我们初步的目标函数。
3.1 初始目标函数(最小割 MinCut \text{MinCut} MinCut方法)
对于无向赋权图 Graph ( X , E ) \operatorname{Graph}(X, E) Graph(X,E) 进行切分的目标是将 G G G 划分成相互无连接的 k k k 个子 图, 每个子图包含点的集合 A 1 , A 2 , ⋯ , A k A_{1}, A_{2}, \cdots, A_{k} A1,A2,⋯,Ak, 且满足 A i ∩ A j = ϕ , A 1 ∪ A 2 ∪ ⋯ ∪ A k = V A_{i} \cap A_{j}=\phi, A_{1} \cup A_{2} \cup \cdots \cup A_{k}=V Ai∩Aj=ϕ,A1∪A2∪⋯∪Ak=V 。
对于任意两个子图点的集合 A , B ⊂ V , A ∩ B = ϕ A, B \subset V, A \cap B=\phi A,B⊂V,A∩B=ϕ, 定义 A A A 和 B B B 之间的切图权重为:
W ( A , B ) = ∑ i ∈ A , j ∈ B , w i j W(A, B)=\sum_{i \in A, j \in B,} w_{i j} W(A,B)=i∈A,j∈B,∑wij
对于 k k k 个子图点的集合 A 1 , A 2 , ⋯ , A k A_{1}, A_{2}, \cdots, A_{k} A1,A2,⋯,Ak, 定义切图 c u t c u t cut 为:
cut ( A 1 , A 2 , ⋯ , A k ) = 1 2 ∑ i = 1 k W ( A i , A ˉ i ) \operatorname{cut}\left(A_{1}, A_{2}, \cdots, A_{k}\right)=\frac{1}{2} \sum_{i=1}^{k} W\left(A_{i}, \bar{A}_{i}\right) cut(A1,A2,⋯,Ak)=21i=1∑kW(Ai,Aˉi)
其中 A ˉ i \bar{A}_{i} Aˉi 为 A i A_{i} Ai, 的补集, 即除了子集 A j A_{j} Aj, 以外的其他 X X X 的子集的并集。
因此,我们可以进一步得到初步离散优化问题,即最小割目标函数:
min C u t ( V ) ⇒ min ∑ v i ∈ A k , v j ∈ A ˉ k , e i j ∈ E w i j \min C u t(V) \Rightarrow \min \sum_{v_{i} \in A_{k}, v_{j} \in \bar{A}_{k}, e_{i j} \in E} w_{i j} minCut(V)⇒minvi∈Ak,vj∈Aˉk,eij∈E∑wij
3.2 引入指示向量( indicator vector \text{indicator vector} indicator vector)
得到最小割目标函数后,我们发现其约束 v i ∈ A k , v j ∈ A ˉ k , e i j ∈ E v_{i} \in A_{k}, v_{j} \in \bar{A}_{k}, e_{i j} \in E vi∈Ak,vj∈Aˉk,eij∈E 比较模糊,较难求解,因此我们需要定性地引入指标向量来细化目标函数。
3.2.1 先讨论只有两个类的情况( c = 2 c=2 c=2)
目标函数为: min Cut ( V ) ⇔ min Cut ( A , A ˉ ) ⇔ min 1 2 ∑ v i ∈ A , v j ∈ A ˉ , e i j ∈ E w i j \min \operatorname{Cut}(V) \Leftrightarrow\min \operatorname{Cut}(A, \bar{A}) \Leftrightarrow\min \frac{1}{2} \sum_{v_{i} \in A, v_{j} \in \bar{A}, e_{i j} \in E}{w_{i j}} minCut(V)⇔minCut(A,Aˉ)⇔min21∑vi∈A,vj∈Aˉ,eij∈Ewij
我们定义指示向量 f = ( f 1 , f 2 , … , f n ) T ∈ N n f=\left(f_{1}, f_{2}, \ldots, f_{n}\right)^{T} \in N^{n} f=(f1,f2,…,fn)T∈Nn
f i = { 1 if v i ∈ A 0 if v i ∈ A ˉ f_{i}= \begin{cases}1 & \text { if } v_{i} \in A \\ 0 & \text { if } v_{i} \in \bar{A}\end{cases} fi={10 if vi∈A if vi∈Aˉ
因此目标函数转变为:
min 1 2 ∑ v i ∈ A , v j ∈ A ˉ , e i j ∈ E w i j ⇔ min 1 2 ∑ i = 1 n ∑ j = 1 n w i j ( f i − f j ) 2 \min \frac{1}{2} \sum_{v_{i} \in A, v_{j} \in \bar{A}, e_{i j} \in E} w_{i j} \Leftrightarrow \min \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} w_{i j}\left(f_{i}-f_{j}\right)^{2} min21vi∈A,vj∈Aˉ,eij∈E∑wij⇔min21i=1∑nj=1∑nwij(fi−fj)2
接下来我们展开 1 2 w i j ( f i − f j ) 2 \frac{1}{2} w_{i j}\left(f_{i}-f_{j}\right)^{2} 21wij(fi−fj)2 二次项: 1 2 ∑ i = 1 n ∑ j = 1 n w i j ( f i − f j ) 2 = 1 2 ∑ i = 1 n ∑ j = 1 n ( w i j f i 2 − 2 f i f j w i j + w i j f j 2 ) = 1 2 ( ∑ i = 1 n d i f i 2 − ∑ i , j = 1 n 2 f i f j w i j + ∑ j = 1 n d j f j 2 ) = 1 2 ( 2 ∑ i = 1 n d i f i 2 − 2 ∑ i , j = 1 n f i f j w i j ) = ∑ i = 1 n d i f i 2 − ∑ i , j = 1 n f i f j w i j = ∑ i = 1 n f i d i f i − ∑ i , j = 1 n f i w i j f j = f T D f − f T W f = f T L f \begin{aligned} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} w_{i j}\left(f_{i}-f_{j}\right)^{2} &=\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n}\left(w_{i j} f_{i}^{2}-2 f_{i} f_{j} w_{i j}+w_{i j} f_{j}^{2}\right) \\ &=\frac{1}{2}\left(\sum_{i=1}^{n} d_{i} f_{i}^{2}-\sum_{i, j=1}^{n} 2 f_{i} f_{j} w_{i j}+\sum_{j=1}^{n} d_{j} f_{j}^{2}\right) \\ &=\frac{1}{2}\left(2 \sum_{i=1}^{n} d_{i} f_{i}^{2}-2 \sum_{i, j=1}^{n} f_{i} f_{j} w_{i j}\right) \\ &=\sum_{i=1}^{n} d_{i} f_{i}^{2}-\sum_{i, j=1}^{n} f_{i} f_{j} w_{i j}=\sum_{i=1}^{n} f_{i} d_{i} f_{i}-\sum_{i, j=1}^{n} f_{i} w_{i j} f_{j} \\ &=f^{T} D f-f^{T} W f \\ &=f^{T} L f \end{aligned} 21i=1∑nj=1∑nwij(fi−fj)2=21i=1∑nj=1∑n(wijfi2−2fifjwij+wijfj2)=21(i=1∑ndifi2−i,j=1∑n2fifjwij+j=1∑ndjfj2)=21(2i=1∑ndifi2−2i,j=1∑nfifjwij)=i=1∑ndifi2−i,j=1∑nfifjwij=i=1∑nfidifi−i,j=1∑nfiwijfj=fTDf−fTWf=fTLf
其中, D D D 为度矩阵, W W W 为邻接矩阵(相似矩阵),而 L = D − W L=D-W L=D−W 为 L a p l a c i a n Laplacian Laplacian矩阵
因此,原目标函数等价于: arg min A ⊂ V C u t ( V ) ⇔ arg min f i ∈ N n 1 2 ∑ i = 1 n ∑ j = 1 n w i j ( f i − f j ) 2 ⇔ arg min f i ∈ N n f T L f \begin{gathered} \underset{A \subset V}{\arg \min } C u t(V) \Leftrightarrow \underset{f i \in N^{n}}{\arg \min } \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} w_{i j}\left(f_{i}-f_{j}\right)^{2} \Leftrightarrow \underset{f_{i} \in N^{n}}{\arg \min } f^{T} L f \\ \end{gathered} A⊂VargminCut(V)⇔fi∈Nnargmin21i=1∑nj=1∑nwij(fi−fj)2⇔fi∈NnargminfTLf
我们通过引入布尔指示向量将一个抽象的切割函数 C u t ( V ) C u t(V) Cut(V) 转化为具体可求解的 f T L f f^{T} L f fTLf 。但是这是一个离散优化函数,无法对其求导。
3.2.2 有多个类的多聚类( c c c 取任意)
对于多聚类问题,我们要聚 c c c个类 ( k = 1 , 2 , … , c ) (k=1,2, \ldots, c) (k=1,2,…,c) ,因此我们仅仅需要将原来一个指示向量扩展为 c c c 个指示向量组合成的指示矩阵 H H H即可,其余步骤一样。
首先,我们定义指示向量 h k = ( h ( 1 , k ) , h ( 2 , k ) , … , h ( n , k ) ) T ∈ N n × 1 h_{k}=\left(h_{(1, k)}, h_{(2, k)}, \ldots, h_{(n, k)}\right)^{T} \in N^{n \times 1} hk=(h(1,k),h(2,k),…,h(n,k))T∈Nn×1 (其中: k = 1 , 2 , … , c k=1,2, \ldots, c k=1,2,…,c )并满足如下公式: h i k = { 1 if v i ∈ A k 0 otherwise ( i = 1 , … , n ; k = 1 , … , c ) h_{i k}=\left\{\begin{array}{ll} 1 & \text { if } v_{i} \in A_{k} \\ 0 & \text { otherwise } \end{array} \quad(i=1, \ldots, n ; k=1, \ldots, c)\right. hik={10 if vi∈Ak otherwise (i=1,…,n;k=1,…,c)
将这 c c c 个指示向量 h k h_{k} hk 组合成一个指示矩阵 H ∈ N n × c H \in N^{n \times c} H∈Nn×c,矩阵 H H H 当中的每一列指示向量 正交 ( o r t h o n o r m a l orthonormal orthonormal) 于其他任何一列非线性相关向量。(注:不代表 H H H一定是正交矩阵)
Tr ( H T H ) = n > 0 \operatorname{Tr}\left(H^{T} H\right)=n>0 Tr(HTH)=n>0
因此我们可以得到如下目标函数:
arg min A 1 , … , A c C u t ( A 1 , … , A c ) ⇔ arg min H ∈ R n × c Tr ( H T L H ) s.t Tr ( H T H ) = n \begin{aligned} \underset{A 1, \ldots, A_{c}}{\arg \min } C u t\left(A_{1}, \ldots, A_{c}\right) \Leftrightarrow \underset{H \in R^{n \times c}}{\arg \min } \operatorname{Tr}\left(H^{T} L H\right) & \\ \text { s.t } \operatorname{Tr}\left(H^{T} H\right)=n \\ & \end{aligned} A1,…,AcargminCut(A1,…,Ac)⇔H∈Rn×cargminTr(HTLH) s.t Tr(HTH)=n
但上面的目标函数存在一定局限,最小割得到的分割结果往往更倾向于将所连边最少且边权值较低的孤立点分割出来。如下图所示。
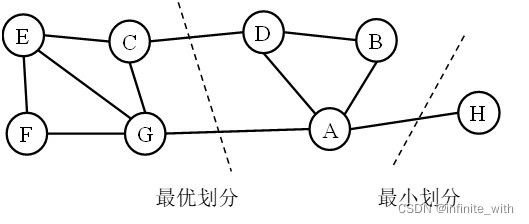
因此我们需要加入其它限制以改进目标函数分割效果。
3.3 改进(RatioCut与Ncut)
为了达到均衡的效果,我们很容易想到在原目标函数(切成每个子图的代价)的基础上除以切图后每个子图的规模。
==如何度量切图后子图的规模? ==
- 从顶点数的角度思考可以想到用子图的顶点数作为该子图的规模。
- 从边的角度思考可以想到用子图的边权和作为子图的规模。
两种度量方式用数学语言有如下定义:
子 图 A 的 势 ∣ A ∣ : = t h e n u m b e r o f v e r t i c e s i n A 子 图 A 的 体 积 vol ( A ) : = ∑ v i ∈ A d i 子图 A 的势 |A|:= the number of vertices in A \\ 子图 A 的体积 \operatorname{vol}(A):=\sum_{v_{i} \in A} d_{i} 子图A的势∣A∣:=thenumberofverticesinA子图A的体积vol(A):=vi∈A∑di
我们可以得到如下两个改进后的目标函数RatioCut(比例切割)与Ncut(归一化切割):
RatioCut ( A 1 , A 2 , … , A c ) : = ∑ k = 1 c C u t ( A k , A ˉ k ) ∣ A k ∣ = 1 2 ∑ k = 1 c W ( A k , A ˉ k ) ∣ A k ∣ Ncut ( A 1 , A 2 , … , A c ) : = ∑ k = 1 c C u t ( A k , A ˉ k ) vol ( A k ) = 1 2 ∑ k = 1 c W ( A k , A ˉ k ) vol ( A k ) \begin{aligned} &\operatorname{RatioCut}\left(A_{1}, A_{2}, \ldots, A_{c}\right):=\sum_{k=1}^{c} \frac{C u t\left(A_{k}, \bar{A}_{k}\right)}{\left|A_{k}\right|}=\frac{1}{2} \sum_{k=1}^{c} \frac{W\left(A_{k}, \bar{A}_{k}\right)}{\left|A_{k}\right|} \\ &\operatorname{Ncut}\left(A_{1}, A_{2}, \ldots, A_{c}\right):=\sum_{k=1}^{c} \frac{C u t\left(A_{k}, \bar{A}_{k}\right)}{\operatorname{vol}\left(A_{k}\right)}=\frac{1}{2} \sum_{k=1}^{c} \frac{W\left(A_{k}, \bar{A}_{k}\right)}{\operatorname{vol}\left(A_{k}\right)} \end{aligned} RatioCut(A1,A2,…,Ac):=k=1∑c∣Ak∣Cut(Ak,Aˉk)=21k=1∑c∣Ak∣W(Ak,Aˉk)Ncut(A1,A2,…,Ac):=k=1∑cvol(Ak)Cut(Ak,Aˉk)=21k=1∑cvol(Ak)W(Ak,Aˉk)
四、目标函数求解
下面,我们先从非标准化 R a t i o C u t RatioCut RatioCut目标函数讲起。
4.1 R a t i o C u t RatioCut RatioCut目标函数的近似解
4.1.1 二聚类( c = 2 c=2 c=2)
m i n A ⊂ V R a t i o C u t ( A , A ˉ ) \underset{A \subset V}{ min} \text{ } RatioCut(A,\bar{A}) A⊂Vmin RatioCut(A,Aˉ)
上节我们推导出
min C u t ( V ) ⇔ min f T L f \min \;Cut(V) \Leftrightarrow\min \; f^TLf minCut(V)⇔minfTLf
我们用拉格朗日乘子转化为无约束问题后可以得到一个有趣的结论。现在我们可以得到等价的完整目标函数:
min A ⊂ V RatioCut ( A , A ˉ ) ⇔ min f ∈ R n f T L f s.t f ⊥ 1 ( t h a t i s f T 1 = 0 ) f T f = n ( f T f > 0 ) \begin{aligned} \min _{A \subset V} \operatorname{RatioCut}(A, \bar{A}) \Leftrightarrow & \min _{f \in R^{n}} f^{T} L f \\ & \text { s.t } f \perp 1 \quad(that \text{ }is \text{ }f^T1=0)\\ & f^{T} f=n \quad\left(f^{T} f>0\right) \end{aligned} A⊂VminRatioCut(A,Aˉ)⇔f∈RnminfTLf s.t f⊥1(that is fT1=0)fTf=n(fTf>0)
使用拉格朗日乘子将约束问题转化为无约束问题
有约束的目标函数我们不会做,我们可以转化为无约束问题,因此目标函数可以转化为如下 L a g r a n g i a n Lagrangian \text{ } Lagrangian 函数 L ( f , λ ) L(f,\lambda) L(f,λ):
L ( f , λ ) : = f T L f − λ ( f T 1 ) − λ ( f T f − n ) = f T L f − λ ( f T f − n ) \begin{aligned} L(f, \lambda):=& f^{T} L f-\lambda\left(f^{T} 1\right)-\lambda\left(f^{T} f-n\right) \\ =& f^{T} L f-\lambda\left(f^{T} f-n\right) \\ \end{aligned} L(f,λ):==fTLf−λ(fT1)−λ(fTf−n)fTLf−λ(fTf−n)
等价将目标约束问题转换:
min f ∈ R n L ( f , λ ) ⇔ min f ∈ R n f T L f s.t f ⊥ 1 ( that is f T 1 = 0 ) f T f = n ( f T f > 0 ) \begin{aligned} \min _{f \in R^{n}} L(f, \lambda) \Leftrightarrow &\min _{f \in R^{n}} f^{T} L f \\ \text { s.t }& f \perp 1\left(\text { that is } f^{T} 1=0\right) \\ & f^{T} f=n \quad\left(f^{T} f>0\right) \end{aligned} f∈RnminL(f,λ)⇔ s.t f∈RnminfTLff⊥1( that is fT1=0)fTf=n(fTf>0)
现在我们得到无约束且连续的目标函数,由于二次型函数是天然的凸函数 亦可导,可以快速找到全局最优解,只需要令其导数为 0 即可得到极值。
(1) 求微分
d L ( f , λ ) = d [ f T L f − λ ( f T f − n ) ] = d ( f T L f − λ f T f ) = d ( f T ) L f + f T L ( d f ) − λ d ( f T ) f − λ f T ( d f ) = ( d f ) T L f + f T L ( d f ) − λ ( d f ) T f − λ f T ( d f ) = tr [ ( d f ) T L f + f T L ( d f ) − λ ( d f ) T f − λ f T ( d f ) ] = tr [ ( d f ) T L f ] + tr [ f T L ( d f ) ] − λ ⋅ tr [ ( d f ) T f ] − λ ⋅ tr [ f T ( d f ) ] = tr [ f T L T ( d f ) ] + tr [ f T L ( d f ) ] − λ ⋅ tr [ f T ( d f ) ] − λ ⋅ tr [ f T ( d f ) ] = tr [ f T ( L T + L ) ( d f ) − 2 λ f T ( d f ) ] = [ f T ( L T + L ) − 2 λ f T ] d f = [ 2 f T L T − 2 λ f T ] d f \begin{aligned} d L(f, \lambda) &=d\left[f^{T} L f-\lambda\left(f^{T} f-n\right)\right]=d\left(f^{T} L f-\lambda f^{T} f\right) \\ &=d\left(f^{T}\right) L f+f^{T} L(d f)-\lambda d\left(f^{T}\right) f-\lambda f^{T}(d f) \\ &=(d f)^{T} L f+f^{T} L(d f)-\lambda(d f)^{T} f-\lambda f^{T}(d f) \\ &=\operatorname{tr}\left[(d f)^{T} L f+f^{T} L(d f)-\lambda(d f)^{T} f-\lambda f^{T}(d f)\right] \\ &=\operatorname{tr}\left[(d f)^{T} L f\right]+\operatorname{tr}\left[f^{T} L(d f)\right]-\lambda \cdot \operatorname{tr}\left[(d f)^{T} f\right]-\lambda \cdot \operatorname{tr}\left[f^{T}(d f)\right] \\ &=\operatorname{tr}\left[f^{T} L^{T}(d f)\right]+\operatorname{tr}\left[f^{T} L(d f)\right]-\lambda \cdot \operatorname{tr}\left[f^{T}(d f)\right]-\lambda \cdot \operatorname{tr}\left[f^{T}(d f)\right] \\ &=\operatorname{tr}\left[f^{T}\left(L^{T}+L\right)(d f)-2 \lambda f^{T}(d f)\right] \\ &=\left[f^{T}\left(L^{T}+L\right)-2 \lambda f^{T}\right] d f \\ &=\left[2 f^{T} L^{T}-2 \lambda f^{T}\right] d f \end{aligned} dL(f,λ)=d[fTLf−λ(fTf−n)]=d(fTLf−λfTf)=d(fT)Lf+fTL(df)−λd(fT)f−λfT(df)=(df)TLf+fTL(df)−λ(df)Tf−λfT(df)=tr[(df)TLf+fTL(df)−λ(df)Tf−λfT(df)]=tr[(df)TLf]+tr[fTL(df)]−λ⋅tr[(df)Tf]−λ⋅tr[fT(df)]=tr[fTLT(df)]+tr[fTL(df)]−λ⋅tr[fT(df)]−λ⋅tr[fT(df)]=tr[fT(LT+L)(df)−2λfT(df)]=[fT(LT+L)−2λfT]df=[2fTLT−2λfT]df
(2) 求得导数
由标量微分 d y = f ′ ( x ) d x dy = f'(x)dx dy=f′(x)dx推导出向量微分 d y = ( d y d x ) T d x dy = (\frac{dy}{dx})^Tdx dy=(dxdy)Tdx得:
d L ( f , λ ) d f = [ 2 f T L T − 2 λ f T ] T = 2 L f − 2 λ f = 0 ⇒ L f = λ f \begin{aligned} \frac{d L(f, \lambda)}{d f} &=\left[2 f^{T} L^{T}-2 \lambda f^{T}\right]^{T}=2 L f-2 \lambda f=0 \\ & \Rightarrow L f=\lambda f \end{aligned} dfdL(f,λ)=[2fTLT−2λfT]T=2Lf−2λf=0⇒Lf=λf
我们得到了一个惊人的结论!!当 L a g r a n g e Lagrange Lagrange乘子 λ \lambda λ是拉普拉斯矩阵 L L L的特征值( e i g e n v a l u e eigenvalue eigenvalue)且指示向量 f f f是 L L L的特征向量( e i g e n v e c t o r eigenvector eigenvector)时,函数有极值。
那么,这个函数的极值到底是什么呢?
在等式两边,分别左乘 f T f^T fT凑成目标函数形式后为:
f T L f = λ f T f = λ n f^TLf=\lambda f ^Tf=\lambda n fTLf=λfTf=λn
因为 n = ∣ V ∣ n=|V| n=∣V∣是常数,显然取决于目标函数值大小的元素是 λ \lambda λ,即
m i n f T L f f T f = min λ min \frac{f^TLf}{f^Tf}=\min \lambda minfTffTLf=minλ
也就是说 L L L的特征值 λ \lambda λ越大,目标函数值越大;特征值 λ \lambda λ越小,目标函数值越小。
渐渐的,我们发现原来的连续优化问题已经转化成了特征分解问题。
那么 λ \lambda λ的最小值是多少呢? λ m i n = 0 λ_{min} =0 λmin=0
令拉普拉斯矩阵的第二小特征值作为目标函数最优值。
对于二聚类( c = 2 c=2 c=2)问题,这个很好做,毕竟我们的解向量 f ∈ R n f\in R^n f∈Rn
,因此最简单粗暴的定性方法是判断 f i f_i fi是否大于等于0,即
{ v i ∈ A if f i ≥ 0 v i ∈ A ˉ if f i < 0 \begin{cases}v_{i} \in A & \text { if } f_{i} \geq 0 \\ v_{i} \in \bar{A} & \text { if } f_{i}<0\end{cases} {vi∈Avi∈Aˉ if fi≥0 if fi<0
4.1.2 多聚类( c c c取任意值)
RatioCut ( A 1 , … , A c ) = ∑ k = 1 c h i T L h i = ∑ k = 1 c ( H T L H ) i i = Tr ( H T L H ) \text { RatioCut }\left(A_{1}, \ldots, A_{c}\right)=\sum_{k=1}^{c} h_{i}^{T} L h_{i}=\sum_{k=1}^{c}\left(H^{T} L H\right)_{i i}=\operatorname{Tr}\left(H^{T} L H\right) RatioCut (A1,…,Ac)=k=1∑chiTLhi=k=1∑c(HTLH)ii=Tr(HTLH)
由于指示矩阵 H H H中向量之间的正交性,我们可以得到如下完整目标函数:
arg min H ∈ R n × c Tr ( H T L H ) s.t H T H = I [ Tr ( H T H ) > 0 ] \begin{aligned} &\underset{H \in R^{n \times c}}{\arg \min } \operatorname{Tr}\left(H^{T} L H\right) \\ &\text { s.t } H^{T} H=I \quad\left[\operatorname{Tr}\left(H^{T} H\right)>0\right] \end{aligned} H∈Rn×cargminTr(HTLH) s.t HTH=I[Tr(HTH)>0]
类似的,可以推出:
m i n T r ( H T L H ) ⇔ m i n λ min\text{ }Tr(H^T LH)⇔minλ min Tr(HTLH)⇔minλ
由于特征值 λ \lambda λ(也是拉格朗日乘子)在这里的物理意义代表切图的代价,因此我们可以将前 k k k小特征值对应的 k k k个特征向量拼接成一个矩阵 U ∈ R n × k U\in R^{n\times k} U∈Rn×k作为 H ∈ R n × c H\in R^{n\times c} H∈Rn×c的近似解。然后使用传统的 k − m e a n s k-means k−means方法,将连续实数值离散化,将矩阵 U U U的 n n n行向量聚为 c c c行向量,最终得到的 l a b e l label label即为最终聚类结果。
4.2 N c u t Ncut Ncut目标函数的近似解
大家可以按 R a t i d o C u t RatidoCut RatidoCut解法自己推导,下面给出 N c u t Ncut Ncut目标函数:
Ncut ( A 1 , A 2 , … , A c ) : = ∑ k = 1 c Cut ( A k , A ˉ k ) vol ( A k ) = 1 2 ∑ k = 1 c W ( A k , A ˉ k ) vol ( A k ) \operatorname{Ncut}\left(A_{1}, A_{2}, \ldots, A_{c}\right):=\sum_{k=1}^{c} \frac{\operatorname{Cut}\left(A_{k}, \bar{A}_{k}\right)}{\operatorname{vol}\left(A_{k}\right)}=\frac{1}{2} \sum_{k=1}^{c} \frac{W\left(A_{k}, \bar{A}_{k}\right)}{\operatorname{vol}\left(A_{k}\right)} Ncut(A1,A2,…,Ac):=k=1∑cvol(Ak)Cut(Ak,Aˉk)=21k=1∑cvol(Ak)W(Ak,Aˉk)
具体代码实现可以看看这篇博客:
谱聚类的成功之处在于它没有很强的假设,相比 k − m e a n s k-means k−means假设聚类的数据分布是 凸 凸 凸的,谱聚类可以解决很普遍的聚类问题。
只要保证相似图是稀疏的,即使对于大数据集,谱聚类也可以有效地实现。一旦选择了相似图,我们只需解决一个线性问题,就不会陷入局部极小值或多次使用不同的初始化重新启动算法。
谱聚类的不足在于图构造方式的不同导致其聚类结果不同,这是其聚类不稳定的重要因素。
谱图理论(spectrum theory)实操
参考文献
[1] Von Luxburg U. A tutorial on spectral clustering[J]. Statistics and computing, 2007, 17(4): 395-416.
[2]https://blog.csdn.net/SL_World/article/details/104423536
[3]从拉普拉斯矩阵说到谱聚类