【DR_CAN-MPC学习笔记】3&4.详细的MPC建模例子和matlab代码
上一篇博客:【DR_CAN-MPC学习笔记】2.最优化数学建模推导
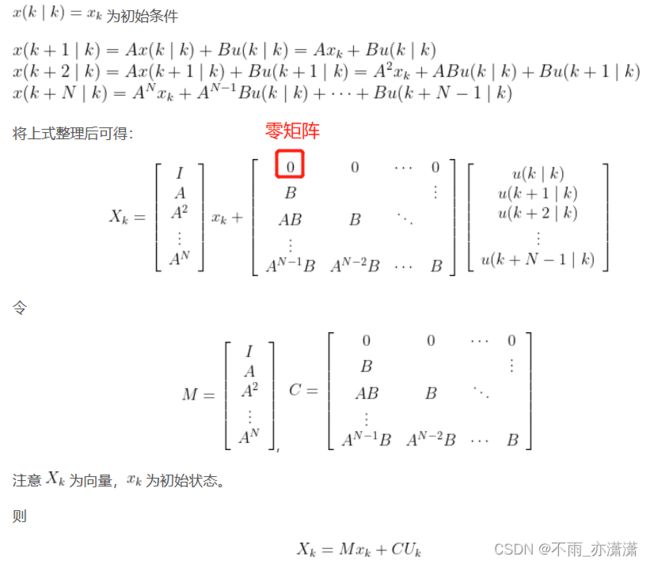
参照二次规划一般形式,详细推导了MPC的数学模型,即最小化代价函数的表达式,最终推导结果为:
![]()
DR_CAN的视频:
【MPC模型预测控制器】3_一个详细的建模例子
【MPC模型预测控制器】3
【MPC模型预测控制器】4_完整案例讲解 - Octave代码
【MPC模型预测控制器】4
离散系统状态空间一般形式:
![]()
其中 ![]() 为状态向量(n×1),
为状态向量(n×1),![]() 为输入向量(p×1),
为输入向量(p×1),![]() 为系统状态矩阵(n×n),
为系统状态矩阵(n×n),![]() 为系统输入矩阵(n×p)。
为系统输入矩阵(n×p)。
单输入二阶系统的例子:
系统状态向量和输入向量的关系:
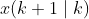 表示在k时刻预测 k+1 时刻的系统状态。
表示在k时刻预测 k+1 时刻的系统状态。- 由于
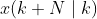 由
由 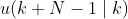 决定,因此不需要
决定,因此不需要 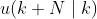 ,所以
,所以 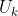 比
比  少一个维度。
少一个维度。 - 因为初始值
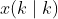 和
和 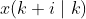 均为 n×1 向量,因此
均为 n×1 向量,因此  为 (N+1)n×1 向量。同理可推出
为 (N+1)n×1 向量。同理可推出 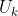 为 Np×1 向量。
为 Np×1 向量。
 为 (N+1)n×n 矩阵。
为 (N+1)n×n 矩阵。 矩阵上面所有的 0 与初始状态
矩阵上面所有的 0 与初始状态 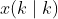 有关(n×1矩阵),
有关(n×1矩阵),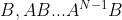 均为 n×p 矩阵,因此
均为 n×p 矩阵,因此  为 (N+1)n×Np 矩阵。
为 (N+1)n×Np 矩阵。
具体可参考上一篇博客的推导(【DR_CAN-MPC学习笔记】2.最优化数学建模推导):
分析过程:
回到单输入二阶系统的例子,![]() ,
,![]() ,n = 2,p = 1,假设预测区间 N=3 ,
,n = 2,p = 1,假设预测区间 N=3 ,
整理一下维度:
| = | + | |||||
| (N+1)n×1 | = | (N+1)n×n | n×1 | + | (N+1)n×Np | Np×1 |
| 8×1 | = | 8×2 | 2×1 | + | 8×3 | 3×1 |
对于系统输出方程: ![]() ,参考值
,参考值 ![]() ,误差
,误差 ![]() ,代价函数为:
,代价函数为:
代价函数 = 误差加权和 + ![]() 输入加权和 +
输入加权和 + ![]() 终端误差,其中
终端误差,其中 ![]() 和
和 ![]() 为权重系数矩阵且均为对角矩阵。
为权重系数矩阵且均为对角矩阵。
经过简化后消去变量 ![]() (简化过程参考【DR_CAN-MPC学习笔记】2.最优化数学建模推导):
(简化过程参考【DR_CAN-MPC学习笔记】2.最优化数学建模推导):
![]()
由上式可见,![]() 只包含了初始状态项
只包含了初始状态项 ![]() 和输入项
和输入项 ![]() ,对
,对 ![]() 进行最优化可以得到输入项
进行最优化可以得到输入项 ![]() 。
。
矩阵 ![]() 与
与 ![]() 有关:
有关:
其中 ![]() 和
和 ![]() 是原来两个权重矩阵
是原来两个权重矩阵 ![]() 和
和 ![]() 的增广形式:
的增广形式:
矩阵计算较为复杂,可用编程求解。
例子代码:
![]()
控制目标:设计合适的 ![]() 使得
使得 ![]() 随着
随着 ![]() 的增加,趋近于0。引入误差
的增加,趋近于0。引入误差 ![]() :
:
![]()
![]() 为目标值,控制目标为令误差接近0。
为目标值,控制目标为令误差接近0。
状态矩阵(n×k):
![]()
![]()
...
![]()
输入矩阵(p×k):
![]()
![]()
...
![]()
状态方程:
![]()
例如:k=1 时,![]() 表示第2列
表示第2列 ![]()
回到单输入二阶系统的例子:
![]() 为系统状态变量权重矩阵,
为系统状态变量权重矩阵, ![]() 为系统输入变量权重矩阵,
为系统输入变量权重矩阵,![]() 为终端权重矩阵。
为终端权重矩阵。
DR_CAN给出了Octave代码,在Matlab中也可以运行。下面的代码是我在此基础上修改后的单输入例子的代码,后面也有介绍如何修改为多输入系统。
传送门:(二输入系统)【MPC模型预测控制器】4_Octave代码
代码一共由三个部分组成,分别为主程序:MPC_Test.m,以及两个函数:MPC_Matrices.m和Prediction.m
MPC_Test.m
设置初始参数:
%% 清屏
clear;
close all;
clc;
%% 加载 optim package,若使用matlab,则注释掉此行
pkg load optim;
%% 第一步,定义状态空间矩阵
%% 定义状态矩阵 A, n x n 矩阵
A = [1 0.1; 0 2];
n= size (A,1); % 计算矩阵第一个维度的长度
%% 定义输入矩阵 B, n x p 矩阵
B = [0; 0.5];
p = size(B,2); % 计算矩阵第二个维度的长度
%% 定义Q矩阵,n x n 矩阵
Q=[1 0; 0 1];
%% 定义F矩阵,n x n 矩阵
F=[1 0; 0 1];
%% 定义R矩阵,p x p 矩阵
R=[0.1];
%% 定义step数量k
k_steps=100;
%% 定义矩阵 X_K, n x k 矩 阵
X_K=zeros(n,k_steps);
%% 初始状态变量值, n x 1 向量
X_K(:,1)=[20;-20]; % 初始状态不为0,控制目标为0
%% 定义输入矩阵 U_K, p x k 矩阵
U_K=zeros(p,k_steps);
%% 定义预测区间K
N=5;
%% Call MPC_Matrices 函数 求得 E,H矩阵
[E,H]=MPC_Matrices(A,B,Q,R,F,N);
%% 计算每一步的状态变量的值
for k = 1 : k_steps
%% 求得U_K(:,k)
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);
%% 计算第k+1步时状态变量的值
X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));
end
%% 绘制状态变量和输入的变化
subplot(2, 1, 1);
hold;
for i =1 :size (X_K,1)
plot(X_K(i,:));
end
legend("x1","x2")
hold off;
subplot(2, 1, 2);
hold;
for i =1 : size(U_K,1)
plot(U_K(i,:));
end
legend("u1")
%% 作者:DR_CAN https://www.bilibili.com/read/cv16891782 出处:bilibili分析:
注释掉以下行,即输入设为0,可单独运行:
N=5;
[E,H]=MPC_Matrices(A,B,Q,R,F,N);
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);得到:
由上图可见,![]() 均趋于无穷,因为初始状态不为0且输入为0.
均趋于无穷,因为初始状态不为0且输入为0.
接下来设置合适的输入使得状态值趋于0.
代价函数:
![]()
![]() 与初始状态有关,不影响代价函数,因此控制目标为最小化
与初始状态有关,不影响代价函数,因此控制目标为最小化 ![]() .
.
![]()
预测了N项,但结果只取第一项 ![]() .
.
![]()
矩阵 ![]() 在之前已经分析过了:
在之前已经分析过了:
矩阵的计算用 MPC_Matrices 函数解决,即代码:
[E,H]=MPC_Matrices(A,B,Q,R,F,N);功能:输入矩阵 A,B,Q,R,F 和预测区间 N ,输出矩阵 E,H。具体过程参考下面的 MPC_Matrices.m 文件。接下来进行预测:
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);MPC_Matrices.m
function [E , H]=MPC_Matrices(A,B,Q,R,F,N)
n=size(A,1); % A 是 n x n 矩阵, 得到 n
p=size(B,2); % B 是 n x p 矩阵, 得到 p
M=[eye(n);zeros(N*n,n)]; % 初始化 M 矩阵. M 矩阵是 (N+1)n x n的,
% 它上面是 n x n 个 "I", 这一步先把下半部
% 分写成 0
C=zeros((N+1)*n,N*p); % 初始化 C 矩阵, 这一步令它有 (N+1)n x NP 个 0
% 定义M 和 C
tmp=eye(n); %定义一个n x n 的 I 矩阵
% 更新M和C
for i=1:N % 循环,i 从 1到 N
rows =i*n+(1:n); %定义当前行数,从i x n开始,共n行
C(rows,:)=[tmp*B,C(rows-n, 1:end-p)]; %将c矩阵填满
tmp= A*tmp; %每一次将tmp左乘一次A
M(rows,:)=tmp; %将M矩阵写满
end
% 定义Q_bar和R_bar
Q_bar = kron(eye(N),Q);
Q_bar = blkdiag(Q_bar,F);
R_bar = kron(eye(N),R);
% 计算G, E, H
G=M'*Q_bar*M; % G: n x n
E=C'*Q_bar*M; % E: NP x n
H=C'*Q_bar*C+R_bar; % NP x NP
end
%%作者:DR_CAN https://www.bilibili.com/read/cv16891782 出处:bilibiliPrediction.m
function u_k= Prediction(x_k,E,H,N,p)
U_k = zeros(N*p,1); % NP x 1
U_k = quadprog(H,E*x_k); % 求出代价函数最小时U_k的数值
u_k = U_k(1:p,1); % 取第一个结果
end
%%作者:DR_CAN https://www.bilibili.com/read/cv16891782 出处:bilibili分析:
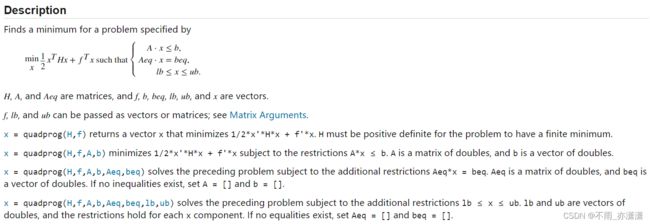
quadprog:matlab自带的最优化函数
运行结果:
![]()
由上图所示,状态值 ![]() 趋于0.
趋于0.
以上为单输入系统的例子。
二输入例子:
代码修改一下,也可以用于多输入,比如:
修改矩阵 A,B,R,Q,F,R ,使得 ![]() 变化得更快(通过对矩阵Q的设置),且降低能耗减小
变化得更快(通过对矩阵Q的设置),且降低能耗减小 ![]() 初始值(系统的输入一般是耗能的部分,通过对矩阵R的设置)
初始值(系统的输入一般是耗能的部分,通过对矩阵R的设置)
修改后的 MPC_Test.m:(其余不变)
%% 清屏
clear;
close all;
clc;
%% 加载 optim package,若使用matlab,则注释掉此行
% pkg load optim;
%% 第一步,定义状态空间矩阵
%% 定义状态矩阵 A, n x n 矩阵
% A = [1 0.1; 0 2];
A = [1 0.1; -1 2];
n= size (A,1); % 计算矩阵维度
%% 定义输入矩阵 B, n x p 矩阵
% B = [0; 0.5];
B=[0.2 1; 0.5 2];
p = size(B,2);
%% 定义Q矩阵,n x n 矩阵
% Q=[1 0; 0 1];
Q=[100 0; 0 1]; % 更加看重x_1的变化
%% 定义F矩阵,n x n 矩阵
% F=[1 0; 0 1];
F=[100 0; 0 1];
%% 定义R矩阵,p x p 矩阵
% R=[0.1];
R=[1 0; 0 0.1]; % 减小能耗,减小输入u_1
%% 定义step数量k
k_steps=100;
%% 定义矩阵 X_K, n x k 矩 阵
X_K = zeros(n,k_steps);
%% 初始状态变量值, n x 1 向量
X_K(:,1) =[20;-20];
%% 定义输入矩阵 U_K, p x k 矩阵
U_K=zeros(p,k_steps);
%% 定义预测区间K
N=5;
%% Call MPC_Matrices 函数 求得 E,H矩阵
[E,H]=MPC_Matrices(A,B,Q,R,F,N);
%% 计算每一步的状态变量的值
for k = 1 : k_steps
%% 求得U_K(:,k)
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);
%% 计算第k+1步时状态变量的值
X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));
end
%% 绘制状态变量和输入的变化
subplot(2, 1, 1);
hold;
for i =1 :size (X_K,1)
plot(X_K(i,:));
end
legend("x1","x2")
hold off;
subplot(2, 1, 2);
hold;
for i =1 : size (U_K,1)
plot(U_K(i,:));
end
legend("u1","u2")
%% 作者:DR_CAN https://www.bilibili.com/read/cv16891782 出处:bilibili![]()
由上图所示,![]() 迅速趋近于0. 相比于 R=[0.1 0; 0 0.1] 时,R=[1 0; 0 0.1] 时的输入
迅速趋近于0. 相比于 R=[0.1 0; 0 0.1] 时,R=[1 0; 0 0.1] 时的输入 ![]() 减小,但
减小,但 ![]() 趋近于0的速度变缓。由此也可以看出MPC的最优化的决策结果不是绝对的。
趋近于0的速度变缓。由此也可以看出MPC的最优化的决策结果不是绝对的。