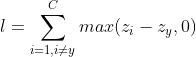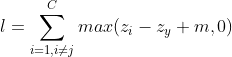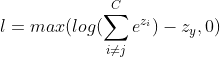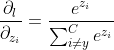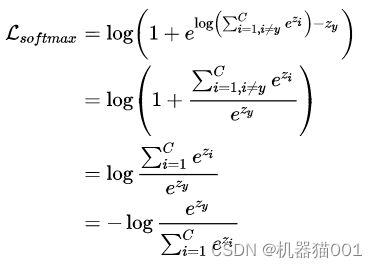softmax交叉熵损失函数的深度理解

 0、前言

        最近拜读了一名优秀学者的博士毕业论文，深受启发。论文题目《基于深度学习的人脸认证方法研究》。损失函数是控制整个深度神经网络训练的中枢，该论文将深入探究了深度学习中损失函数的机理，并把之前广泛用于通用图像识别的损失函数和多种用于度量学习的损失函数改造得更加适合人脸认证模型的训练。该论文对传统的 Softmax 交叉熵损失函数以及新提出的一系列改进进行了大量的理论分析，有别于传统理论更多的偏向概率解释，该论文中提出的理论分析大多是基于特征、权重之间的几何关系与统计量进行的，由于特征与权重相比于Softmax 概率更加底层，因此能够得到更多的数学结论。

       本人水平有限，此处只能说参考前辈的毕业论文，总结一些学习笔记，如有冒犯请联系删除。

1、引出部分

        损失函数是指导整个神经网络训练的一个部件，如果说各模型结构是神经网络的躯干，那损失函数就是神经网络的大脑。一个完整的神经网络会输出一系列的数值，将这些数值与理想数值进行比对后向这些数值输出梯度，之后通过反向传播算法将梯度传播到所有层进行更新。一般来说，在设计损失函数时要与测试指标进行匹配，即测试时使用什么样的指标就用什么样的损失函数。例如评价指标为均方误差时，使用均方误差作为损失函数效果最好；在评价指标为平均绝对误差时，使用绝对值误差效果更好；在指标为各类别同等权重时，对训练样本进行均匀采样可以大幅提升效果[1]。

        一般而言，最优化的问题通常需要构造一个目标函数，然后寻找能够使目标函数取得最大/最小值的方法。目标函数往往难以优化，所以有了各种relax、smooth的方法，例如使用L1范数取代L0范数、使用sigmoid取代阶跃函数等等。

        那么我们就要思考一个问题：使用神经网络进行多分类（假设为类）时的目标函数是什么？神经网络的作用是学习一个非线性函数，将输入转换成我们希望的输出。在不考虑网络结构只考虑分类器（也就是损失函数）的话，最简单的方法莫过于直接输出一维的类别序号。而这个方法的缺点显而易见：我们事先并不知道这些类别之间的关系，而这样做默认了相近的整数的类是相似的，为什么第2类的左右分别是第1类和第3类，也许第2类跟第5类更为接近呢？

        为了解决这个问题，可以将各个类别的输出独立开来，不再只输出1个数而是输出个分数（某些文章中叫作logit[1]），每个类别占据一个维度，这样就没有谁与谁更近的问题了。那么如果让一个样本的真值标签（ground-truth label）所对应的分数比其他分数更大，就可以通过比较个分数的大小来判断样本的类别了。沿用《基于深度学习的人脸认证方法研究》使用的名词 ，称真值标签对应的类别分数为目标分数(target score)，其他的叫非目标分数(non-target score)。这样我们就得到了一个优化目标：输出C个分数，使目标分数比非目标分数更大。

      数学表述就是：,其中y为真值对应的序号，为目标分数，即样本的真值标签（ground-truth label）所对应的分数比其他分数更大。

      基于该目标设定目标函数，得到了目标函数之后，就要考虑优化问题了。我们可以给一个负的梯度，给其他所有一个正的梯度，经过梯度下降法，即可使升高而 下降。为了控制整个神经网络的幅度，不可以让无限地上升或下降，所以我们利用max函数，让在刚刚超过时就停止上升，即一旦超过损失值就为0：

        然而这样做往往会使模型的泛化性能比较差，我们在训练集上才刚刚让超过 ，那测试集很可能就不会超过。借鉴svm里间隔的概念，我们添加一个参数，让比  大过一定的数值才停止，即：

        这样我们就推导出了hinge loss。

2、softmax交叉熵损失函数的推导 

        hinge loss在SVM时代大放异彩，但在神经网络时代就不好用了呢？主要就是因为svm时代我们用的是二分类，通过使用一些小技巧比如1 vs 1、1 vs n等方式来做多分类问题。而直接把hinge loss应用在多分类上的话，当类别数C特别大时，会有大量的非目标分数得到优化，这样每次优化时的梯度幅度不等且非常巨大，极易梯度爆炸。其实要解决这个梯度爆炸的问题也不难，将这个损失函数换个说法就是一旦超过的最大值，即输出C个分数，使目标分数比最大的非目标分数大，就停止上升。跟之前相比，多了一个限制词“最大的”，但其实我们的目标并没有改变，“目标分数比最大的非目标分数更大”实际上等价于“目标分数比所有非目标分数更大”。这样我们的损失函数就变成了：

        在优化这个损失函数时，每次最多只会有一个+1的梯度和一个-1的梯度进入网络，梯度幅度得到了限制。但这样修改每次优化的分数过少，会使得网络收敛极其缓慢，这时就又要祭c出smooth大法了。那么max函数的smooth版是什么？有同学会脱口而出：softmax！恭喜你答错了...

        这里出现了一个经典的歧义，softmax实际上并不是max函数的smooth版，而是one-hot向量（最大值为1，其他为0）的smooth版。其实从输出上来看也很明显，softmax的输出是个向量，而max函数的输出是一个数值，不可能直接用softmax来取代max。max函数真正的smooth版本是LogSumExp函数。

        （1）第一次smooth化：使用LogSumExp函数取代max函数。

而 LogSumExp函数的导数恰好为softmax函数：

         经过这一变换，给予非目标分数的1的梯度将会通过LogSumExp函数传播给所有的非目标分数，各个非目标分数得到的梯度是通过softmax函数进行分配的，较大的非目标分数会得到更大的梯度使其更快地下降。这些非目标分数的梯度总和为1，目标分数得到的梯度为-1，总和为0，绝对值和为2，这样我们就有效地限制住了梯度的总幅度。

        （2）第二次smooth化：使用softplus函数取代ReLU函数

        注意到ReLU函数也有一个smooth版，即softplus函数，使用softplus函数之后，即使超过了LogSumExp函数，仍会得到一点点梯度让继续上升，这样其实也是变相地又增加了一点，使得泛化性能有了一定的保障。替换之后就可以得到：

         这个就是大家所熟知的softmax交叉熵损失函数了。

        在经过两步smooth化之后，我们将一个难以收敛的函数逐步改造成了softmax交叉熵损失函数，解决了原始的目标函数难以优化的问题。从这个推导过程中我们可以看出smooth化不仅可以让优化更畅通，而且还变相地在类间引入了一定的间隔m，从而提升了泛化性能。

        注意：smooth化就是相当于在类间引入一定的间隔m，提升泛化性能。

参考文献：[1] F. Wang, X. Xiang, C. Liu, et al. Regularizing face verification nets for pain intensity regression[C]. IEEE International Conference on Image Processing, 2017, 1087-1091