Lumerical Python API学习（七）——可视化几何

Optimizable Geometry - Python API

来自 https://support.lumerical.com/hc/en-us/articles/360052044913-Optimizable-Geometry-Python-API

本节介绍了使用 lumopt 的基于形状和拓扑的逆向设计的详细信息。 作为先决条件，请熟悉光子逆向设计（photonic inverse design）并了解 lumopt 工作流程（photonic inverse design）的基础知识。

以下示例有助于为此处提供的信息提供上下文。

• Inverse design optimization - list of examples

一、形状

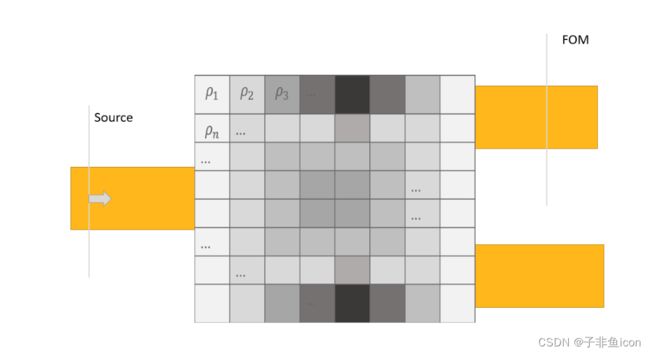
基于形状的优化允许用户采用强大的现有设计并提高其性能。 约束可以很容易地包含在参数化中，例如制造的设计规则。 为此，用户需要通过形状函数 s§ 参数化他们的几何形状并提供 p 值的界限。 少数几何类 FunctionDefinedPolygon 支持这一点，它们接受 Python 参数函数，以及 ParamterizedGeometry 接受 Python API 函数。 FDTD 用于计算 FOM(s§)。

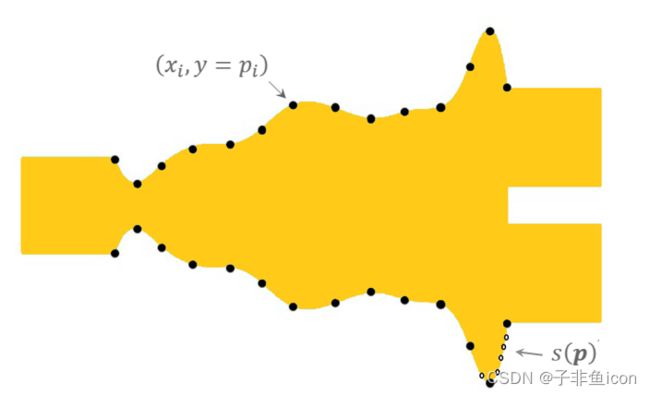
图 1：形状参数和形状函数

伴随方法动机部分（Adjoint method motivation）描述了参数如何通过介电常数进入方程。当用户定义参数化几何时，需要一个额外的步骤，我们称为 d_eps_calculation，以确定每个参数的变化如何改变麦克斯韦方程中的介电常数和随后的形状导数。这是通过对模拟进行网格划分并返回 ϵ(x,y,z) 来完成的，但无需运行求解器。由于必须对每个参数执行此操作，因此包含更多参数需要额外的成本；不过，与运行模拟相比，这应该很小；然而，在大型 3D 模拟中，即使是短暂的，这个网格划分步骤也可能是密集的。如果您需要帮助提高 d_eps 计算的性能和并行化，请联系 Lumerical 支持。有关形状导数近似方法的更多信息，请参阅 Owen Miller 论文的第 5 章（Chpt 5 of Owen Miller’s thesis.）。

重要的是要考虑参数的选择可能过于严格，并且基于梯度的技术本质上取决于初始条件。参数和初始条件的更好选择并不总是很明显，因此可能需要进行一些实验才能获得最佳性能。

形状几何类

对于每个几何类，用户必须传递形状函数、参数界限、几何规范和材料属性。验证您的几何形状是否平滑变化并且对于可接受的参数的任何组合不会自相交非常重要，因为这会在梯度计算中产生不连续性。样条点的界限与可能有问题的参数不同。当端点被钳位时，这可能会导致不连续性，采用“非结样条”通常可以避免这些错误。通过可视化从可能的有界参数集实现的不同形状，可以识别和避免大多数这些错误。

Functiondefinedpolygon

这个 python 类采用优化参数的用户定义函数。该函数通过返回一组顶点来定义多边形，作为坐标对 np.array([(x0,y0),…,(xn,yn)]) 的 numpy 数组，其中顶点必须在计数器中排序顺时针方向。

from lumopt.geometries.polygon import FunctionDefinedPolygon 
class  FunctionDefinedPolygon(func,
 initial_params,
 bounds,
 z,
depth,
 eps_out,
 eps_in,
 edge_precision,
dx,
deps_num_threads) 

: func : function
function(parameters) - 返回 s§ ， np.array([(x0,y0),…,(xn,yn)]) 的坐标元组按逆时针排序。
通常，多边形点 p 的子集将用作样条技术的参数，以对这些值进行上采样并创建更平滑的曲线。 这个用户定义的函数是一个常见的错误来源。

: initial_params: np.array
func 接受的形式的参数，用于定义初始几何。 Size = [1, n_param]

: bounds: np.array
一组定义每个参数的最小值和最大值的元组。Size = [2, n_param]

: z : float
沿 z 轴的多边形中心。Default = 0.0

: depth: float
沿 z 轴的多边形跨度。

: eps_out: float
多边形周围材料的介电常数。

: eps_in: float
多边形材料的介电常数。

: edge_precision: int
沿每条边的正交点数，用于使用形状导数近似方法计算 FOM 梯度。

: dx: float > 0.0
使用介电常数扰动计算 FOM 梯度的步长。 Default = 1e-5

: deps_num_threads: int, optional
d_eps 计算中要使用的线程数。 这利用了任务管理器，并更改了您的资源配置。 默认情况下，这将连续执行，但可以通过将其设置为大于 1 来同时使用更多内核。这是一个高级的实验性功能，具有一些相关的额外开销； 因此，需要进行测试和基准测试。 如果发生意外终止，则必须手动修复更新。 Resource configuration elements and controls. Default = 1

ParameterizedGeometry

from lumopt.geometries.parameterized_geometry import ParameterizedGeometry 
class ParameterizedGeometry(func,
                            initial_params,
                            bounds,
 dx,
deps_num_threads) 

: func : python API function
function(parameters, fdtd, only_update, (optional arguments))
这个函数不如 FunctionDefinePolygon 简洁，但更直观、更灵活。 它允许用户调用 API 方法，就像您使用 lsf 脚本命令来设置和更新几何图形而不是传递 (x,y) 顶点一样。 标志“only_update”用于避免频繁重新创建参数化几何，这会降低性能。 当标志为真时，假定几
何图形已至少添加到 CAD 一次。 有关其用法的示例，请参见光栅耦合器的逆向设计。 Inverse design of grating coupler.

: initial_params: np.array
func 接受的形式的参数，用于定义初始几何。Size = [1, n_param]

: bounds: np.array
一组定义每个参数的最小值和最大值的元组。Size = [2, n_param]

: dx: float > 0.0
使用介电常数扰动计算 FOM 梯度的步长。Default = 1e-5

: deps_num_threads: int, optional
d_eps 计算中要使用的线程数。 这利用了作业管理器，并更改了您的资源配置。 默认情况下，这将连续执行，但可以通过将其设置为大于 1 来同时使用更多内核。这是一个高级的实验性功能，具有一些相关的额外开销； 因此，需要进行测试和基准测试。 如果发生意外终止，则必须手动修复更新。 Resource configuration elements and controls. Default = 1

形状注意事项

从 2D 到 3D

通过 MODE varFDTD 和 FDTD 支持二维形状优化。使用 varFDTD 将自动折叠 z 方向上的材料和几何贡献，以更准确地反映有效指数。 FDTD 仅使用材料折射率，忽略第三维。对于面内集成光子元件，varFDTD 提供了获得准确介电常数值的最直接途径。在这种情况下也可以使用 FDTD，但确定有效指数取决于用户。在传播不完全在平面内的情况下，例如光栅耦合器示例，需要 FDTD。要使用 varFDTD，请在优化类中设置 use_varFDTD = True。

在形状优化中，从 2D 迁移到 3D 很简单，因为所有支持的几何类都是可迁移的。唯一需要的更新是将基本文件监视器和模拟区域从 2D 更改为 3D FDTD。应为 eps_in 和 eps_out 指定散装材料指数，因为几何贡献会自动合并到更新方程中。我们发现 2D 中的高性能设备与 3D 中的设备性能之间存在很强的相关性；然而，当考虑到新的损失机制时，预计在转向 3D 时 FOM 会降低。由于 3D 优化所需的复杂性和时间，我们建议从 2D 开始，然后将这些优化的结构导入 3D 以进行最终的简化优化运行。

GDS 导出

导出优化的几何图形时，我们建议使用加密的 GDS 导出脚本，概述并在此处下载：

• GDSII Export Script

二、GDS导出

此处参考：FDTD Solutions时域有限差分法仿真学习相关操作（一）——GDS导出

三、拓扑

在拓扑优化中，用户不需要对几何进行参数化，从而简化了工作流程； 然而，模拟需要执行一些更复杂的步骤来生产物理上可实现的设备。 要设置拓扑优化，只需在相关 2D 或 3D 几何类中定义可优化的封装和材料，概述如下。 离散优化体积中的每个 FDTD 网格单元都成为一个参数。 这种技术通常可以扩展到数千个参数，但使用伴随方法，每次迭代我们仍然只需要 2 次模拟来计算梯度。 此外，由于介电常数值是优化参数，因此与麦克斯韦方程有直接联系，因此无需执行 d_eps 作为计算。

图 2：拓扑优化示意图

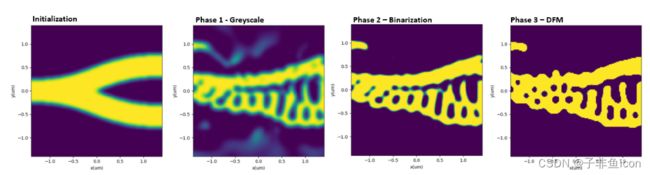
在初始化部分，我们描述了设置的重要方面，以及如何提供初始条件。 一旦优化运行，它会分两到三个步骤进行。 首先是参数在纤芯和包层指数之间连续变化的灰度阶段。 接下来，运行二值化阶段以强制网格单元采用纤芯或包层指数。 最后，实现了制造步骤的可选设计。 在此步骤中，将惩罚函数添加到 FOM。 惩罚函数的大小由违反最小特征尺寸约束的程度决定。 最后，我们将讨论如何从 2D 迁移到 3D，并将您的设计导出到 GDS。

Topology Geometry Classes 拓扑几何类

TopologyOptimization2D

此类用于 2D 模拟。

from lumopt.geometries.topology import TopologyOptimization2D 
class TopologyOptimization2D(params,
                             eps_min,
                             eps_max,
                             x, y, z,
                             filter_R, 
                             eta,
                             beta,
                             min_feature_size) 

: params : np.array
定义初始几何的初始参数。 Size = [n_x, n_y]

: eps_min : float
芯材的介电常数

: eps_max: float
包层的介电常数

: x: np.array
参数和 FDTD 单元的 x 位置，以 [m] 为单位。

: y : np.array
参数和 FDTD 单元的 y位置，以 [m] 为单位。

: z : float
拓扑对象的 Z 位置，单位为 [m]。 Default 0.0

: filter_R: float
Heaviside 过滤器的半径，以 [m] 为单位。 以灰度显示。Outlined in greyscale. Default = 200e-9

: eta : float
Heaviside 过滤器的 Eta 参数。 如果 eta <0.5，则将二值化阈值向 eps_min 移动，如果 eta >0.5，则向 eps_max 移动。Default = 0.5

: beta: float
Heaviside 过滤器的 Beta 参数。 这是使用的起始值，但 beta 参数在二值化阶段上升到 ~1000。Default = 1

: min_feature_size: float, optional
DFM 阶段的最小特征尺寸。 小于该值的特征将在最后的 DFM 阶段受到惩罚。 必须为 filter_R < min_feature_size < 2.0 * filter_R。 值 0.0 将禁用 DFM 阶段。 Default = 0.0

TopologyOptimization3DLayered

此类用于 3D 模拟，并以与 2D 几何相同的方式操作，不同之处在于 z 现在是所需的点的 numpy数组，并且优化区域是一个体积。 为了将场结果减少到 XY 平面，沿 z 进行积分。 图层的图案针对每个网格单元进行了优化，但不是针对每个网格单元单独优化：即它不是完整的 3D 体素化拓扑几何，目前不支持该功能。

from lumopt.geometries.topology import TopologyOptimization3DLayered 
class TopologyOptimization3DLayered(params, 
eps_min,
 eps_max,
x, y, z,
 filter_R,
eta,
beta,
min_feature_size) 

: params : np.array
定义初始几何的初始参数。 Size = [n_x, n_y, n_z]

: eps_min : float
芯材的介电常数

: eps_max: float
包层的介电常数

: x: np.array
参数和 FDTD 单元的 x 位置，以 [m] 为单位。

: y : np.array
参数和 FDTD 单元的y位置，以 [m] 为单位。

: z : np.array
参数和 FDTD 单元的 z位置，以 [m] 为单位。

: filter_R: float
Heaviside 过滤器的半径，以 [m] 为单位。 以灰度显示。Outlined in greyscale. Default = 200e-9

: eta : float
Heaviside 过滤器的 Eta 参数。 如果 eta <0.5，则将二值化阈值向 eps_min 移动，如果 eta >0.5，则向 eps_max 移动。 Default = 0.5

: beta: float
Heaviside 过滤器的 Beta 参数。 这是使用的起始值，但 beta 参数在二值化阶段上升到 ~1000。Default = 1

: min_feature_size: float, optional
DFM 阶段的最小特征尺寸。 小于该值的特征将在最后的 DFM 阶段受到惩罚。 必须为 filter_R < min_feature_size < 2.0 * filter_R。 值 0.0 将禁用 DFM 阶段。Default = 0.0

Running

本节介绍拓扑优化的各个阶段。

图 3：拓扑优化步骤

初始化

重要的是 FDTD 模拟中定义的网格与 Python 中定义的优化参数精确匹配。 为此，请确保在可优化面积（footprint）上定义统一的网格。 python参数可以定义如下。

#Footprint and pixel size  足迹和像素大小
size_x = 3000        #< Length of the device (in nm). Longer devices typically lead to better performance 
# #< 设备长度（以 nm 为单位）。 更长的设备通常会带来更好的性能
delta_x = 25        #< Size of a pixel along x-axis (in nm) 沿 x 轴的像素大小（以 nm 为单位）
size_y = 3000        #
# #<沿 y 轴的范围（以 nm 为单位）。 当使用对称时，这应该是大小的一半。
delta_y = 25        #< Size of a pixel along y-axis (in nm) 
size_z = 240        #< Size of device in z direction 
delta_z = 40        #< Size of a pixel along z-axis (in nm) 

x_points=int(size_x/delta_x)+1 
y_points=int(size_y/delta_y)+1 
z_points=int(size_z/delta_z)+1 

#Convert to SI position vectors 
x_pos = np.linspace(-size_x/2,size_x/2,x_points)*1e-9 
y_pos = np.linspace(-size_y/2,size_y/2,y_points)*1e-9 
z_pos = np.linspace(-size_z/2,size_z/2,z_points)*1e-9 

在生成基本文件的 lumerical 脚本中，确保网格匹配。 还允许使用 Python 函数或基本文件等替代方法，但网格和参数值也需要匹配。

#Define footprint 
opt_size_x=3e-6; 
opt_size_y=3e-6; 
opt_size_z=240e-9; 

#Define pixel size 
dx = 25e-9; 
dy = 25e-9; 
dz = 40e-9; 
 
addmesh; 
set('name','opt_fields_mesh'); 
set('override x mesh',true);  set('dx',dx);  
set('override y mesh',true); set('dy',dy);  
set('override z mesh',true); set('dy',dz); 
set('x',0); set('x span',opt_size_x); 
set('y',0); set('y span',opt_size_y); 
set('z',0); set('z span',opt_size_z); 

要设置初始条件，您可以传递与参数大小相同的 np.array。 如果您想从整个可优化域的统一介电常数值开始，这很简单。

##Initial conditions 
#initial_cond = np.ones((x_points,y_points))       #< Start with the domain filled with eps_max 
# #< 以 eps_max 填充的域开头
#initial_cond = 0.5*np.ones((x_points,y_points))   #< Start with the domain filled with (eps_max+eps_min)/2 
#initial_cond = np.zeros((x_points,y_points))      #< Start with the domain filled with eps_min          

或者，在基础模拟中定义一个初始结构，然后传递 None。 在这种情况下，优化器对模拟进行网格划分以确定初始参数集。 这应该是一个包含相关几何图形的结构组，称为 initial_guess.

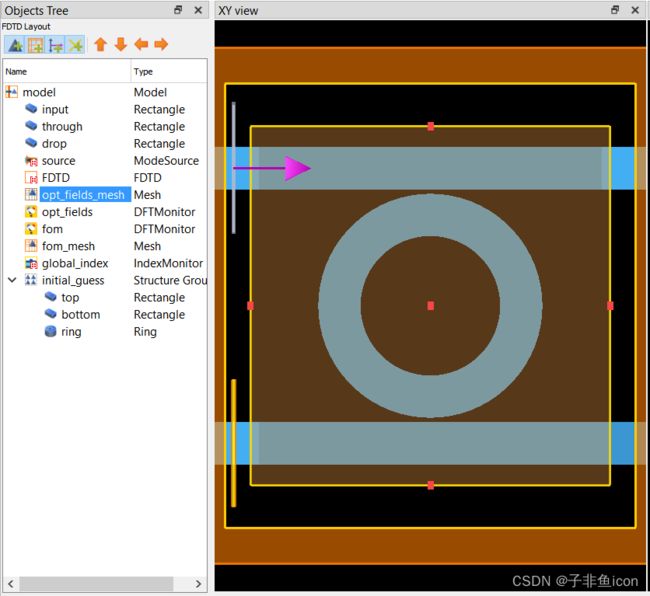
灰度Greyscale

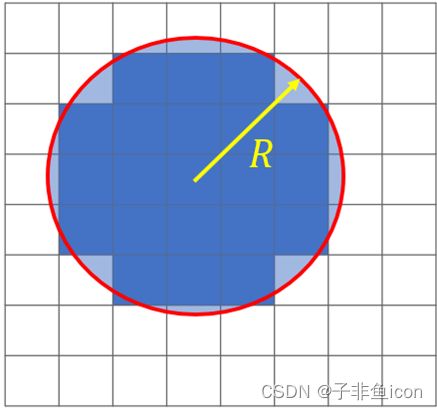
在 python 优化中，每个单元对应一个参数 ρ∈[0,1]，该参数线性映射到 FDTD 中的 ϵ 值。 具有用户指定半径的圆形顶帽卷积（top hat convolution）用于去除无法通过卷积制造的尖角、小孔或岛（sharp corner, small holes, islands）。 根据您的制造工艺，过滤器半径的典型值将在 50 到 500nm 之间。

图 5：顶帽卷积图

在这个优化阶段，FOM 误差趋于非常迅速地减少，但可能需要 100 次迭代才能达到最小值。 灰度期间获得的值通常非常好，但过滤过程不完善，并且会出现中间 eps 值和通过光刻方式无法生产的特征。 以下步骤用于生产可实现的设备。

二值化Binarization

在二值化期间，Heaviside 过滤器将 python 元素的映射更改为 FDTD 介电常数。 在灰度阶段，beta 参数为 1，产生线性映射。 在二值化过程中，beta 参数逐渐增加。 Heaviside 滤波器定义如下，增大 beta 参数会将其从线性映射转换为阶跃函数。


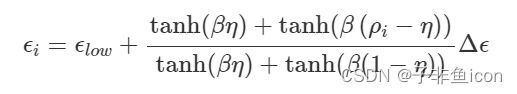
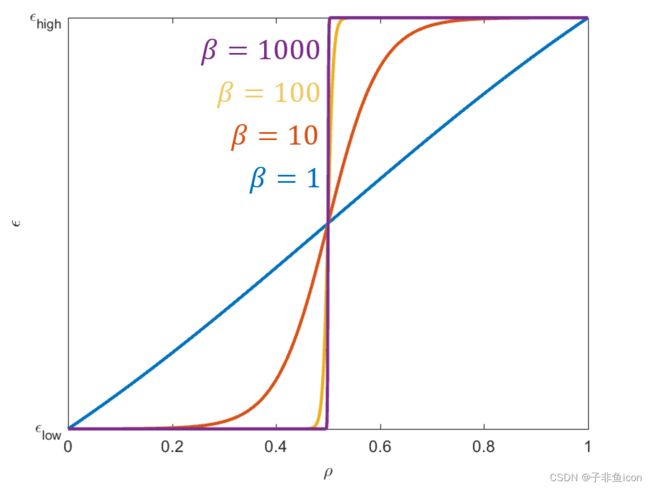
图 6：Heaviside 过滤器

增大 β 将扰乱系统，在 FOM 中产生尖峰。 随后是一组优化迭代以适应扰动，并减少 FOM 误差。 可以通过更改 opt.continuation_max 参数来更改 Beta 增量之间的迭代次数。

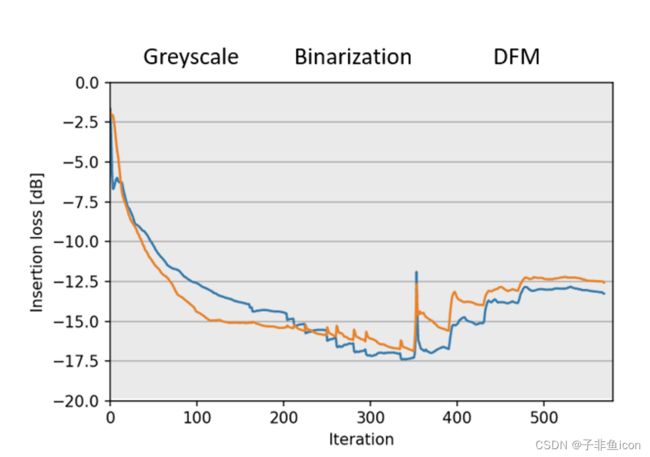
图 7：优化步骤中的 FOM

制造设计（可选）

即使使用 Heaviside 过滤器进行空间过滤，拓扑优化设计也倾向于创建破坏流程设计规则的特征。 为了确保可制造性，我们探索了明确执行特定最小特征尺寸约束的方法。 我们的实现使用了 Zhou 等人发表的技术。 2015 年[1]。 这篇论文的重点是结构力学，因此我们必须进行一些小的调整，以使其可靠地用于光子器件。

1. Zhou, M. et a. “Minimum length scale in topology optimization by geometric constraints”, Comput. Methods in Appl. Mech. Eng 293, 266-282 (2015) 4

主要思想是提出一个指标函数，如果在任何地方都满足最小特征尺寸约束，则该指标函数是最小的。 然后在优化期间将该项作为惩罚项添加到 FOM。 要实现此阶段，请将非零 min_feature_size 约束传递给几何类。

拓扑注意事项

从 2D 到 3D

形状的所有尺寸考虑都适用于拓扑。 我们建议使用 varFDTD 中计算的有效指数作为 2D opt 中的介电常数值，但应使用 FDTD 进行所有拓扑优化。

在拓扑结构中从 2D 到 3D 时，性能并不相关，就像在基于形状的设计中一样。 话虽如此，良好的 2D 结果证明了产生强大的 3D 设计的可能性，这很重要。 如果导入未完全二值化的设计，则 3D 性能改进往往会更快进行，这会放宽 3D 优化器改变参数的能力。 下面概述了将部分二值化的 2D 设计导入 3D。

## First, we specify in which path to find the 2d optimization
## 首先，我们指定在哪个路径中找到 2d 优化
path2d = os.path.join(cur_path,"[Name of 2D opt folder]")

## Next, check the log-file to figure out which iteration we should load from. 
# It is usually best to load something mid-way through the binarization
## 接下来，检查日志文件以确定我们应该从哪个迭代中加载。
# 通常最好在二值化过程中加载一些东西
convergence_data = np.genfromtxt(os.path.join(path2d, 'convergence_report.txt'), delimiter=',')

## Find the first row where the beta value (3rd column) is larger than beta_threshold (here 10)
## 找到 beta 值（第 3 列）大于 beta_threshold（这里为 10）的第一行
beta_threshold = 10
beta_filter = convergence_data[:,2]>beta_threshold
convergence_data = convergence_data[beta_filter,:]  #< Trim data down #< 修剪数据
iteration_number = int(convergence_data[0,0]-2)

## Load the 2d parameter file for the specified iteration
## 加载指定迭代的二维参数文件
geom2d = TopologyOptimization2D.from_file(os.path.join(path2d, 'parameters_{}.npz'.format(iteration_number) ), filter_R=filter_R, eta=0.5)
startingParams = geom2d.last_params     #< Use the loaded parameters as starting parameters for 3d
#< 使用加载的参数作为 3d 的起始参数
startingBeta   = geom2d.beta            #< Also start with the same beta value. One could start with 1 as well.
#< 也以相同的 beta 值开始。 也可以从 1 开始。

导出到 GDS

由于拓扑设计的设备没有明确定义的形状，我们开发了一种替代方法来使用轮廓提取 GDSII 设计。 此功能在以下 KX 页面中进行了概述。