吴恩达深度学习之一《神经网络和深度学习》学习笔记
一、深度学习概论
1.2 什么是神经网络
![]()
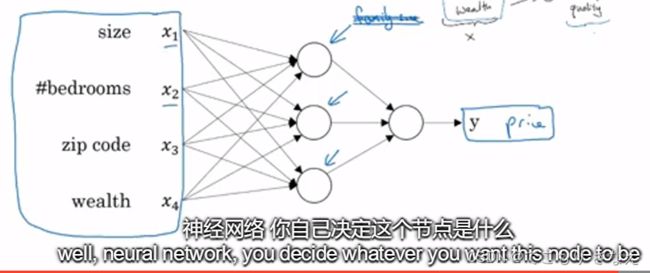
如上图所示的房价预测,我们可以把它的线性回归看作一个神经元构成的神经网络。神经元就是那个圈,是一个用于映射计算的函数。
图中使用的是十分常见的 ReLU函数,全称为修正线性单元(又称线性整流函数),就是一个非负的线性回归,让预测本应<0的部分都等于0
第一层是输入层x,最后一层是输出层y,中间是隐藏层。给你左边这四个房屋特征,预测房价。隐藏层结点用什么函数,有没有含义表示什么含义,都是由你来决定和设计的。比方说第二层三个结点你可以预测家庭人口、步行化程度、学校质量,然后再进一步预测价格。
1.3 用神经网络进行监督学习
1.4 为什么深度学习会兴起
数据规模足够大时,随着数据规模的增大,机器学习模型的表现几乎不变。但越是大规模的神经网络,随着数据规模的增大,越是有更好的表现。当然在小规模时有时机器学习能表现得更好。
另一个原因是函数算法的优化
![]()
如图,sigmoid在两侧梯度趋近0,训练的很慢,而神经网络完全可以在过程中使用很多ReLU,这个训练起来就很快
二、神经网络基础
2.1 二分分类
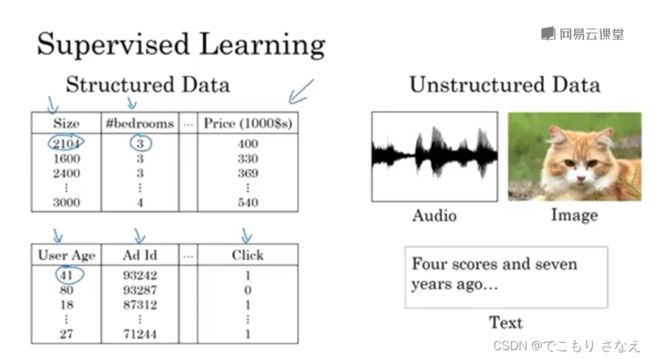
比如彩色图片,像素64x64,RGB三个矩阵构成,每个像素点的值是0到255的灰度级位数。
一张图片就是一个样本,把这个样本的 64*64*3=12288个特征值摞起来就是 n=12288 维的特征向量
注意和机器学习的差别,深度学习中,一列是一个样本,一行是一个特征点
![]()
如图所示是m个样本构成的特征矩阵X,和标签矩阵y
再次注意和机器学习是反着来的,括号上标是第 j 个样本,即一列是一个样本
2.2 logistic回归
回忆机器学习内容
于是 x=0 时 y=0.5,x 正无穷 y 趋近 1,x 负无穷 y 趋近 0
逻辑回归就是假说函数 ![]()
本课程中使用前者写法。后者写法就是 ![]() 令
令![]() ,
,![]() 整合到一起的写法
整合到一起的写法
2.3 logistic回归损失函数
回忆机器学习内容
损失(误差)函数(loss(error) function)是一个样本预测值和实际值间的偏差
代价(成本)函数(cost function)是 m 个样本损失函数的均值
这个函数的问题是 不是一个凹的,他有很多极小值
一般我们使用的损失函数是
![]()
整体取负号是因为 log 在 0 到 1 算出是负的,我们要用正数形式来比较大小
y=0 时,起作用的是后一项,想让 L 趋近 0,也就是让 y帽 趋近0
y=1 时,起作用的是前一项,想让 L 趋近 0,也就是让 y帽 趋近1
这个函数是一个凹函数,有唯一极值点
代价函数就是求和后的均值
2.4 梯度下降法
学习率 α
回忆机器学习内容,就是下山
重复执行如下操作,直到收敛
2.8 计算图的导数计算
![]()
如图正向传播就是带入当前参数,算出代价函数 J = 33
反向传播就是用链式求导来梯度下降,因为隐藏层都是我们设定的函数,所以依照链式求导法则,可以直接对输入层的参数更新
即每次 ![]()
2.9 logistic回归中的反向传播
如图所示,输入层是 偏置单元 x0=1 和 x1、x2,对应参数 b、w1、w2
隐藏层是一层逻辑回归假说函数,图中拆成了两步,第一步线性回归假说函数,第二步sigmoid函数
输出层是 a,a 和 y帽在书写定义上的区分是,a 是每一轮的结果,拿着 a 可以去梯度下降,最后得到的最终结果输出为 y帽
我们要用代价函数的偏导 w = w - dL / dw 来更新参数 w
由![]()
得![]()
得 ![]()
注意sigmoid函数的导数可以用反函数反带回去,所以最后偏导总是可以用 x、y、y帽 来计算
![]()
于是最后
2.10 m个样本的梯度下降
2.9中展示的是用损失函数,即一个样本
实际应当用代价函数
而由代价函数的公式,显然我们可以发现,代价函数的偏导也是损失函数偏导的平均值
一般我们将 J 对某一项的偏导 简记为这一项的微分,比如上式我们一般会将 ![]() 简记为
简记为 ![]()
2.11 向量化
做矩阵操作应该尽可能用numpy
numpy使用了SIMD单指令多数据流,充分利用了CPU/GPU的并行性,其中GPU更适合并行
据博主推断,numpy做一次向量整体操作应该只需要 O(1),而 for 循环需要 O(n)
不难想象 矩阵乘法用 np.dot 应该是 O(n^2),而手写朴素算法的 for 是 O(n^3)
另外要注意 jupyter notebook 中只有 CPU,没有 GPU
2.13 向量化logistic回归
对于 ![]()
显然 m 个样本可以向量化成 ![]()
记作 ![]()
2.14 向量化logistic回归的梯度输出
实际上我前面的这个写法已经是扩展为 n 行了,w 和 x^(i) 都是一个样本的列向量,没有带下标
更进一步地,我们应当把 m 个样本的求和符号去掉
想象一下线代学的 ![]()
不难得到![]()
当然这里也可以不用 1/m sum,用 mean 或者 average 也是可以的
2.15 Python中的广播
比如一个矩阵加一个数,就是这个矩阵每个元素都加这个数
这种整体操作基本是常数级的,因为SIMD
这种拷贝性的整体操作称之为广播
当然并不是什么形式都能拷贝广播
常见的用法是 单个数、行向量、列向量 的广播
如图所示
![]()
吴恩达给出的一个应用是 向量化 计算 元素在列和中所占百分比,如图所示
![]()
需要注意的是,数值轴记作 0 轴,水平轴记作 1 轴
另外一定要注意的是,向量是一种矩阵,是二维数组,而非一维数组!!
一定要养成小心检查维度shape,养成shape、reshape的习惯
在机器学习编程中要尽可能杜绝使用一维数组
2.18 (选修)logistic损失函数的解释
logistic损失函数的本质是在做极大似然估计
极大似然估计即用 θ 表示出似然函数(特定样本下的概率函数),求这个函数的极大值,便可让估计的概率最高,极大值点 θ帽 就是 θ 的极大似然估计
概率中,求似然函数 L(或者P) 的极大值时,一般用 log L 来求导,算极值点
logistic 中的似然函数 即在 不同条件 x 下,对 y 的预测的概率
实际上,可以把这个条件按 y 来分段函数
我们知道我们预测的是 y=1 的概率
于是对 y=1 预测命中的概率是 y帽,对 y=0 预测命中的概率是 1-y帽
数学中的题目,我们都是带入一个特定样本,计算出对 θ 的似然估计
而机器学习中,我们要给出表达式,对一个不确定的样本,让它能直接带表达式直接求
对不确定的样本,带入分段函数求极值并不是一个好的选择,写起来还要加入if之类的逻辑进行分类讨论,可以发现的是,它可以合并成一个函数
![]()
极大似然估计就是让这个函数取极大值
对 P 取log得到的 ![]() 就是我们的损失函数的表达式,就是求其极小值
就是我们的损失函数的表达式,就是求其极小值
对于 m 个样本,它们是独立同分布的,联合概率就是每个样本概率的累乘乘积
求这个联合函数的极大值,取 log,就变成加和形式了
因此,这就是为什么 代价函数 是 m个样本的损失函数的和
值得一提的是,你可能会好奇log的底到底是什么,这个是自由的,只要单调,随便自己想搞什么都行,一般可能会默认用log2方便书写一些
然后需要注意的是,通过这个概率式子,你也可以理解到,所有二分类问题它的损失函数、代价函数都是这种形式,不论你用的是或不是逻辑回归
三、浅层神经网络
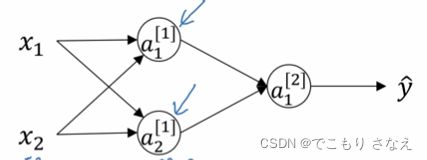
3.1 神经网络概览
![]()
图中的每个神经元我们都设为sigmoid单元
具体来讲,图中每一个神经元做的是 ![]()
规定用上标括号表示第几层的变量(输入层是第 0 层)
图中的过程就是
![]()
![]()
![]()
![]()
计算 ![]() 然后反向传播,得到最终的结果输出为
然后反向传播,得到最终的结果输出为 ![]()
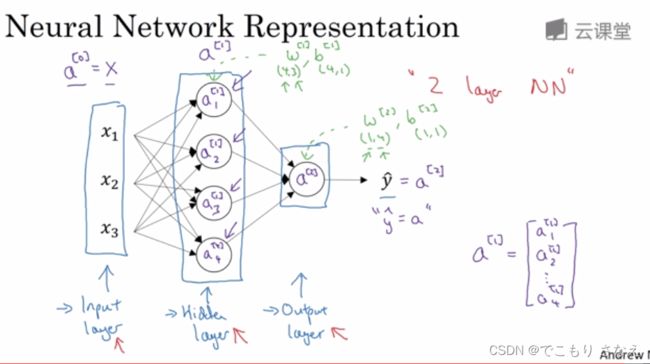
3.2 神经网络表示
如图一层输入层,一层隐藏层,一层输入层
输入是第0层,一般不计入层数,我们一般把图中的神经网络叫做双层神经网络
a 是 activations,叫作激活值,即传入下一层的值
输入层 x 又可记作 ![]()
W的维数中,行数是所在层的结点数,列数是上一层的结点数
第 i 层的参数,和第 i-1 层的激活值 a^i-1 计算,得到本层的激活值 a^i
同层每个激活值按顺序从上到下用下标 1、2、3、... 来表示
下标 i 实际上就是取第 i 行向量
对 W 也是这样,W1 就是用 x 计算 a1 的一行参数
3.3 计算神经网络的输出
W 的一行里的每个元素,是对应上一层各个激活值的参数,W的这一行用作算出本层的一个激活值
显然
![]()
3.4 多个例子中的向量化
进一步,把 m 个样本加入进来
显然
![]() (正向传播总结性最终公式,注意)
(正向传播总结性最终公式,注意)
3.5 向量化实现的解释
前面已经讲过了,再总结一次(概念总结,注意)
![]() :第 k 层,第 j 个样本的第 i 个激活值( i 行 j 列,下同)
:第 k 层,第 j 个样本的第 i 个激活值( i 行 j 列,下同)
![]() :第 k 层,用于计算本层第 i 个激活值
:第 k 层,用于计算本层第 i 个激活值 ![]() 对应于上一层第 j 个激活值
对应于上一层第 j 个激活值 ![]() 的一个参数
的一个参数
A的一行是一个激活值在每一个样本的实际值
A的一列是一个样本的所有激活值
W的一行是用于算得本层一个A的、对应于上一层所有A的参数
W的一列是用于算得本层每个A的、对应于上一层一个A的参数
对 W 我们应该按行分块,对 A 我们应该按列分块
W 乘以上层 A 的一列,就是算出本层 A 的一列,即本层一个样本的所有 A
W 的一行乘以上层 A,就是算出本层 A 的一行,即本层所有样本的一个 A
W 的一行乘以上层 A 的一列,就是算出本层 A 的一个元素,即本层一个样本的一个A,哪一个A取决于 W 的哪一行,哪一个样本取决于上层 A 的哪一列
3.6 激活函数
![]()
如图所示的是四种激活函数(总结性内容,注意)
③ReLU:![]()
④Leaky ReLU:![]()
tanh 函数范围是 [ -1, 1 ]。tanh 函数的表现比 sigmoid 更好,但是二分类输出层一定要用 sigmoid,于是 tanh 就是用于隐藏层。然而二者都有一个问题就是导数趋近0,训练慢(称作饱和神经元),用ReLU会快一些(称作非饱和神经元,实际上ReLU是一个左饱和函数,即导数为0)。但是ReLU在负向导数恒为 0 ,这是一个小小的问题,一般可以尝试一下 带泄露的ReLU 即 Leaky ReLU ,效果会更好一点。
3.7 为什么需要非线性激活函数
对 x 的线性组合的线性组合还是 x 的线性组合
隐藏层如果只用 ReLU 那就是毫无意义的,不论你有多少隐藏层,都和全部删掉没有区别,就和机器学习的逻辑回归是完全一样的,所以你一定要有 tanh
吴恩达表示,ReLU 的唯一用途是用作回归问题的输出层激活函数,比如房价预测
博主的进一步理解
实际上隐藏层如果要用线性单元,应当尽可能只用 Leaky ReLU,因为由链式求导法则,z一旦进入负向,路径中含有 ReLU 的参数将直接收敛,再也不会梯度下降,不会再有任何变化,称作一个死亡的神经元。特别在学习率过大的时候,这个弊端十分明显。还需要注意的是实际上隐藏层只用 ReLU 和删除所有隐藏层并不完全等价。ReLU 并非普通的线性组合,它的负向是 0,只含ReLU其实并不等价于logistic回归。因此,隐藏层如果要用 ReLU 应该只用 Leaky ReLU。然后不妨思考,假设我们允许一层中使用多个激活函数,可以发现一层中出现 >= 2个线性激活函数,就已经是多余了,显然一层中最多 1 个线性激活函数,而且一层中只有1个线性激活函数也是多余的,这层可以删掉,因此一层中至少应当有 1 个非线性激活函数,不然就应该删掉。(总结性内容,注意)
3.8 激活函数的导数
(总结性内容,注意)
对 a = g(z)
①sigmoid 的导数:![]()
②tanh 的导数:![]()
(注:数学上在 0 处导数无定义,计算机中如果你要实现,可以随便定义一个值,这是无关紧要的,很少有正好=0的情况,对于 Leaky ReLU也是同理)
④Leaky ReLU的导数:![]()
3.9 神经网络的梯度下降法
我们可以用 ![]() 表示第 i 层的单元个数
表示第 i 层的单元个数
于是前面讲过的 ![]() 的维数就可以表示为
的维数就可以表示为 ![]()
带入m个样本的向量化反向传播(总结性结论,注意)
对这类问题首先要想清一件事,就是链式求导应该在 求和 的里面,当你需要的时候才会涉及整体取平均值
其次是弄清公式问题,求和怎么转向量化
利用分块矩阵
可以得到 ![]() ,就是求和形式,反过来就是做向量化
,就是求和形式,反过来就是做向量化
其中 ai、bi,可以是等长向量对应相乘,也可以是其中一个是数,另一个是向量。也可以两个都是数
以双层神经网络、二分类任务、所有神经元均为 sigmoid单元 为例
我们有
注意过程中我们一开始是对应项相乘,然后可以转换为与转置向量的内积
有
实际上,只有输出层那里的计算特别一些,从这里开始,我们已经能给出一个统一计算的递推式了
设激活函数为 g(z)
![]() ( 注:dJ 种包含了1/m 不要忘了 )
( 注:dJ 种包含了1/m 不要忘了 )
当然,我们前面假设了同一层用的都是同一个激活函数
当然每个神经元可以用不同的激活函数,这时只需调整一下![]() 即可
即可
![]() 的结果还是作为一个矩阵带回递推式,唯一的差别是
的结果还是作为一个矩阵带回递推式,唯一的差别是![]() 的计算应当对每个行向量
的计算应当对每个行向量![]() 分别用对应的激活函数求导,然后将这些行向量组合成矩阵再带回去
分别用对应的激活函数求导,然后将这些行向量组合成矩阵再带回去
实际上对输出层(第 L 层)我们也可以稍微总结一下公式
![]()
( 注:dJ/dA 就是损失函数基础上换成矩阵并乘上1/m )
( 注:这里和隐藏层的常规公式是一样的,输出层唯一特殊的只有 dJ/dZ )
最后要说的是一个编程中的小问题,对于numpy,如果一个函数的计算结果是向量,它会很糟糕地返回给你一个一维数组,当你不想用reshape这个写法时,可以用keepdims参数,比如np.sum(Z, keepdims=True)
3.11 随机初始化
如图所示,假设箭头指向的两个神经元用的同一个激活函数
如果他们的参数初始值相同,那么将始终计算同一个函数
这两个神经元称作对称的,这是毫无意义的事情
所以我们要随机初始化
令图中 ![]() ,W^[2]同理
,W^[2]同理
注意乘了个 0.01,是因为太大了梯度下降就慢了,接近 0 会好一点
0.01 对浅层神经网络是一个很好的选择
然后其他值的情况将在接下来的课程中介绍
四、深层神经网络
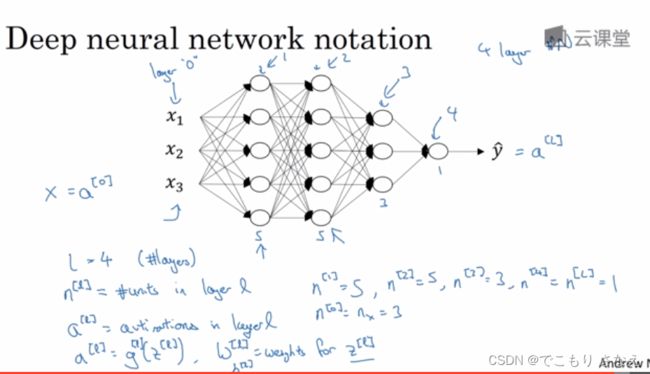
4.1 深层神经网络
层数记作 L,小写 l 表示第几层
每层结点数用 ![]() 表示
表示
输入层可以用 ![]() 或者
或者 ![]() ,输出层如图,可以是
,输出层如图,可以是 ![]() 或者
或者 ![]()
4.3 核对矩阵的维数
(总结性内容,注意!)
![]()
![]()
![]()
![]()
对第 j 个样本,有:(省略了 l,下同,三个维度的混合自己做)
![]()
![]()
![]()
对层中的第 i 个结点,有:
![]() ,对
,对 ![]() 或说
或说 ![]() 就是混合起来的
就是混合起来的 ![]() ,很显然,不再赘述
,很显然,不再赘述
![]()
![]()
用于计算本层第 i 个结点的所有参数:
![]()
用于计算本层所有结点的第 j 个参数(即和上一层第 j 个结点相乘):
![]()
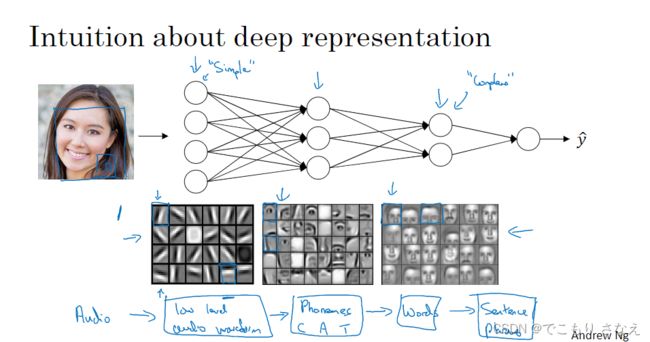
4.4 为什么使用深层表示
随着层数加深,可以对特征的处理逐步细化,比如图像、音频识别中,第一层首先是边缘探测器,探测出面部的一些边缘,然后再识别出眼睛鼻子耳朵这些器官,然后再识别出这些器官的组合,再...
另一种常用的解释是电路理论
![]()
比如说对 y = a xor b xor c xor d
abcd 组合有 0000、0001、0010、...、1111 共 2^n = 16 种,如右图所示,你只用一层,那么你将用 2^n 个单元来表示出所有这些组合
而如左图所示,( a xor b) xor ( c xor d ),组合的组合就变成树形,只需要 n-1 个单元
实际上这就是 树、图 其数据结构本身的用途和优势
4.5 搭建神经网络块
浅层中已讲过正向传播和反向传播,不再赘述
需要注意的是,实际操作中
正向传播传递 A,缓存 Z,反向传播传递 dJ/dA
4.6 前向和反向传播
主要是激活函数不同的问题,吴恩达讲的还是比较粗的,浅层中我已总结过
4.7 参数VS超参数
(重点)首先需要注意的是,神经网络的实际应用中,因为一些原因,我们总是同一层使用相同的激活函数(所以,隐藏层完全不可能用RELU...,另外,也因此随机初始化的必要性不言而喻)
参数 Parameters 包括 W 和 b
超参数 Hyper Parameters 包括:
学习率 α
梯度下降循环次数 iterations
隐藏层数 L
某一隐藏层的神经元数量 ![]()
某一层的激活函数的选择
等等
其他超参数将会在下一个吴恩达课程中具体讲解
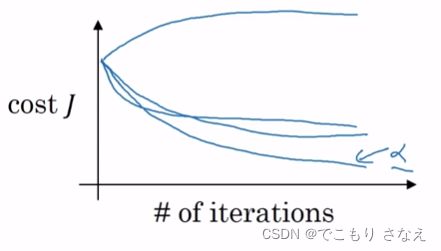
超参数 α 可以通过观察随着 迭代步数,代价函数值的变化 来进行调整
比如上图,你看到代价增大,最后发散,那么不选,再换个 α 试试
比如,某个 α 得到最下面那条线,代价下降得快,收敛得小,那么就用这个 α 了
4.8 这和大脑有什么关系
长得像神经元,然后吸引媒体,就这样,实际也可以说没啥关系吧...

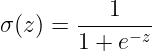
![\large J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log{\hat{y}^{(i)}}+(1-y^{(i)})\log{(1-\hat{y}^{(i)})}]](http://img.e-com-net.com/image/info8/1aa916dd4c1443a7a43fcd133e335b9f.gif)
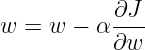
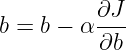
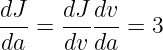
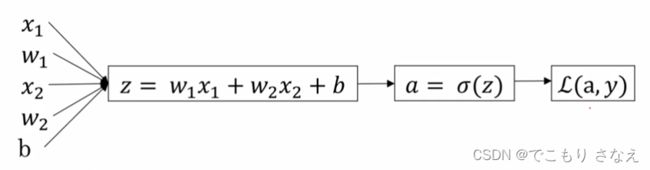
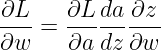
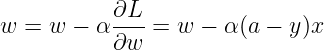
![\large \frac{\partial{J}}{\partial{w}}=\frac{1}{m}\sum_{i=1}^{m}[(\hat{y}^{(i)}-y^{(i)})x^{(i)}]](http://img.e-com-net.com/image/info8/9d0c1b9d9bd44409bbc3ed2e37616f13.gif)
![\large dw=\frac{1}{m}\sum_{i=1}^{m}[(\hat{y}^{(i)}-y^{(i)})x^{(i)}]](http://img.e-com-net.com/image/info8/de396ce33b494f9791f83d161b6824b7.gif)
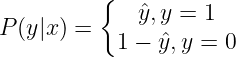
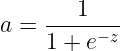

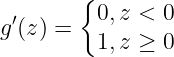
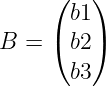
![\large \frac{dJ}{dW^{[2]}}](http://img.e-com-net.com/image/info8/f1348b5ea3684b48bac3338d3ff73d0e.gif)
![\large \frac{dJ}{dW^{[1]}}](http://img.e-com-net.com/image/info8/2bda388a03144051b04c7d3ea4a2806c.gif)
![\large \frac{dJ}{dZ^{[i]}}=\frac{dJ}{dZ^{[i+1]}}W^{[i+1]}{g^{[i]}}'(A^{[i]})](http://img.e-com-net.com/image/info8/43261e6d91c341eb89f1b1a02bf37ebc.gif)
![\large \frac{dJ}{dW^{[L]}}=\frac{dJ}{dZ^{[L]}}A^{[L-1]T}](http://img.e-com-net.com/image/info8/952ce26f7c314ec78131c64cc2f15082.gif)