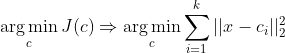【聚类】详解常用的聚类算法（K-Means、DBSCAN等）

• 本文收录于《深入浅出讲解自然语言处理》专栏，此专栏聚焦于自然语言处理领域的各大经典算法，将持续更新，欢迎大家订阅！
• ​个人主页：有梦想的程序星空
• ​个人介绍：小编是人工智能领域硕士，全栈工程师，深耕Flask后端开发、数据挖掘、NLP、Android开发、自动化等领域，有较丰富的软件系统、人工智能算法服务的研究和开发经验。
• ​如果文章对你有帮助，欢迎​关注、​点赞、​收藏、​订阅。

1、聚类的背景概念

聚类是将物理或抽象对象的集合分成由类似的对象组成的多个类的过程。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。聚类是一种运用广泛的探索性数据分析技术，人们对数据产生的第一直觉往往是通过对数据进行有意义的分组，通过对对象进行分组，使相似的对象归为一类，不相似的对象归为不同类。

在无监督学习中，目标通过对无标记数据训练样本的学习来揭示数据内在的性质规律，将数据集中的样本划分为多个不相交的子集，为数据进一步分析提供基础。

聚类的评判标准：簇间相似度高，簇内相似度低的时候效果最好。

2、K-Means聚类算法

聚类原则：以空间中个点为中心进行聚类，对最靠近中心的对象归类。逐次计算各簇中心的值为新的中心值，迭代更新，直至得到最好的聚类结果。

目标函数：各簇成员到其聚类中心的距离的平方和最小，如下所示：

其中，为聚类中心集合，共有个聚类中心。

算法流程：

（1）适当选择个类的初始中心；

（2）在第次迭代中，对任意一个样本，求其到个中心的距离，将该样本归到距离最短的中心所在的类/簇；

（3）利用均值等方法更新该类的中心值；

（4）对于所有的个聚类中心，如果利用（2）（3）的迭代法更新后，聚类中心的位置保持不变，则迭代结束；否则，继续迭代。

KMeans算法的适用场景：它比较适合服从高斯分布的样本数据集的划分。

优点：（1）原理比较简单，实现也是很容易，收敛速度快。（2）算法的可解释度比较强。（3）主要需要调参的参数仅仅是簇数。

缺点：（1）需要事先确定分类的簇数，即k值。（2）采用迭代方法，得到的结果只是局部最优。（3）对初始值的选取比较敏感。当数据量非常大时，算法的时间开销是非常大的（改进：Mini Batch K-Means精确度会降低，在可接受的范围即可））。（4）若簇中含有异常点，将导致均值偏离严重，对噪声和孤立点数据敏感（改进1：离群点检测的LOF算法，通过去除离群点后再聚类，可以减少离群点和孤立点对于聚类效果的影响；改进2：改成求点的中位数，这种聚类方式即K-Mediods聚类（K中值））。（5）对于不是凸的数据集比较难收敛(改进：基于密度的聚类算法更加适合，比如DBSCAN算法)。

 问题1：kmeans算法结果易受初始点影响，该怎么办？

由于kmeans算法结果易受初始点影响，得到的结果是局部最优，为次，我们可以运行n次K-Means算法，每次运行的初始点均为随机生成。然后在n次运行结果中，选取目标函数(代价函数)最小的聚类结果。

问题2：聚类数量k如何确定?

通常在数据集有多少个聚类是不清楚的。对于低维的数据，对其可视化，我们可以通过肉眼观察到有多少个聚类，但这样并不准确，而且大部分数据也无法可视化显示。我们可以通过构建一个代价函数与聚类数量k的关系图，横坐标是聚类数量，每个聚类数量对应的代价函数J均是n次运行的最优结果。

sklearn代码：

sklearn.cluster.KMeans(n_clusters=8)

其中，n_clusters为开始的聚类中心数量，整型，缺省值为8，生成的聚类数，即产生的质心（centroids）数。

方法:

estimator.fit(x)

estimator.predict(x)

estimator.fit_predict(x)：计算聚类中心并预测每个样本属于哪个类别，相当于先调用fit(x)，然后再调用predict(x)。

3、Mini Batch K-Means算法

Mini Batch K-Means算法是K-Means算法的一种优化变种，采用小规模的数据子集(每次训练使用的数据集是在训练算法的时候随机抽取的数据子集)减少计算时间，同时试图优化目标函数；Mini Batch K-Means算法可以减少K-Means算法的收敛时间，而且产生的结果效果只是略差于标准K-Means算法。

算法步骤如下：

    • 首先抽取部分数据集，使用K-Means算法构建出K个聚簇点的模型；

    • 继续抽取训练数据集中的部分数据集样本数据，并将其添加到模型中，分配给距离最近的聚簇中心点；

    • 更新聚簇的中心点值(每次更新都只用抽取出来的部分数据集)  ；

    • 循环迭代第二步和第三步操作，直到中心点稳定或者达到迭代次数，停止计算操作   ------- 这个算法思想类似于SGD算法；

       每次都是使用与上一次不同的抽样数据进行更新簇中心点，可以重复更新循环多次

Mini Batch K-Means减少K-Means算法的收敛时间，而且产生的结果效果只是略差于标准K-Means算法。适用场景：大量数据聚类，效果比K-Means差一些。

4、学习向量化（LVQ）

 LVQ带有类标记，采用迭代优化。样本集，学习效率，初始化原型向量并设置其标记。

假设数据样本带有类别标记，利用这些监督信息来辅助聚类。

5、DBSCAN算法

DBSCAN是基于一组邻域来描述样本集的紧密程度的，参数用来描述邻域的样本分布紧密程度。其中，描述了某一样本的邻域距离阈值，描述了某一样本的距离为的邻域中样本个数的阈值。

DBSCAN的聚类定义很简单：由密度可达关系导出的最大密度相连的样本集合，即为最终聚类的一个类别，或者说一个簇。

这个DBSCAN的簇里面可以有一个或者多个核心对象。如果只有一个核心对象，则簇里其他的非核心对象样本都在这个核心对象的-邻域里；如果有多个核心对象，则簇里的任意一个核心对象的-邻域中一定有一个其他的核心对象，否则这两个核心对象无法密度可达。这些核心对象的-邻域里所有的样本的集合组成的一个DBSCAN聚类簇。

 DBSCAN算法是确定性的，当以相同的顺序给出相同的数据时，总是生成相同的簇。但是，当以不同顺序提供数据时，结果可能不同。

优点：

可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。
可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

缺点：

如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

sklearn代码：

class sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean', algorithm='auto', 
    leaf_size=30, p=None, n_jobs=1)

6、谱聚类

谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高。通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

对象形式：
class sklearn.cluster.SpectralClustering(n_clusters=8, eigen_solver=None, 
    random_state=None, n_init=10, gamma=1.0, affinity='rbf', n_neighbors=10, eigen_tol=0.0, 
    assign_labels='kmeans', degree=3, coef0=1, kernel_params=None, n_jobs=1)
 
函数形式：
sklearn.cluster.spectral_clustering(affinity, n_clusters=8, n_components=None, eigen_solver=None, 
    random_state=None, n_init=10, eigen_tol=0.0, assign_labels='kmeans')

关注微信公众号【有梦想的程序星空】，了解软件系统和人工智能算法领域的前沿知识，让我们一起学习、一起进步吧！