[机器学习]关联挖掘算法Apriori和FP-Growth以及基于Spark 实例

 

目录

 

Apriori 算法

FP-Growth算法

算法原理

步骤1 统计各个商品被购买的频次

步骤2 构建FP树

步骤3 频繁项的挖掘

---

阅读本文需要了解关联挖掘的基本知识，了解关联挖掘的基本原理，参考《[机器学习]关联挖掘介绍》。

Apriori 算法

Apriori算法就是根据有关频繁项集特性的先验知识而命名的。它使用一种称作逐层搜索的迭代方法，k-项集用于探索（k+1）-项集。

首先，找出频繁1-项集的集合．记做L1，L1用于找出频繁2-项集的集合L2，再用于找出L3，如此下去，直到不能找到频繁k-项集。找每个Lk需要扫描一次数据库。

Apriori性质：一个频繁项集的任-子集也应该是频繁项集；任何非频繁项集的超集一定也是非频繁的。

因为这个性质，可以减少数据库扫描的次数。

FP-Growth算法

算法原理

频繁模式增长(frequent-pattern growth)，简称FP-growth。它采取如下分治策略：将提供频繁项集的数据库压缩到一棵频繁模式树（FP-tree），但仍保留项集关联信息。

FP-Growth算法仅仅需要两次扫描数据库，第一次是统计每个商品的频次，用于剔除不满足最低支持度的商品，然后排序得到FreqItems。第二次，扫描数据库构建FP树。

FP-Tree：将事务数据表中的各个事务数据项按照支持度排序后，把每个事务中的数据项按降序依次插入到一棵以 NULL为根结点的树中，同时在每个结点处记录该结点出现的支持度。

算法描述如下：

1、对于每个频繁项，构造它的条件投影数据库和投影FP-tree。

2、对每个新构建的FP-tree重复这个过程，直到构造的新FP-tree为空，或者只包含一条路径。

3、当构造的FP-tree为空时，其前缀即为频繁模式；当只包含一条路径时，通过枚举所有可能组合并与此树的前缀连接即可得到频繁模式。

例子：

假设我们的Transaction数据库有5条交易数据，如下表，其中abcde为5个商品。假设设定minsup = 0.4，即要求至少共同出现2次（0.4*5=2）

id	购买商品
1	a b d
2	b c d
3	a b e
4	a b c
5	b c d

步骤1 统计各个商品被购买的频次

扫描数据库，统计每个商品的频次，并进行按降序排序，显然商品e仅仅出现了一次，不符合minsup,剔除。最终得到的结果如下表：

购买商品	次数
b	5
c	3
d	3
a	3

步骤2 构建FP树

扫描数据库，进行FP树的构建。FP树以root节点为起始，节点包含自身的item和count，以及父节点和子节点。

      首先是第一条交易数据，a b d，结合第一步商品顺序，排序后为b a d，依次在树中添加节点b，父节点为root，最新的的频次为1，然后节点a，父节点为a，频次为1，最后节点d，父节点为b，频次为1。如下图所示：

 

       然后是第二条交易数据，排序后为：b c d。依次添加b，树中已经有节点b，因此更新频次加1，然后是节点c，b节点当前只有子节点d，因此新建节点c，父节点为b，频次为1，最后是d，父节点为c，频次为1。

 

        第三条交易数据，排序后为：b a e。因为e的支持度小于阈值，去掉，只添加b a

 

     第四条交易数据，排序后为：b a c,依次添加

 

      第五条交易数据，排序后为：b c d,依次添加

 

步骤3 频繁项的挖掘

1、商品b频繁项的挖掘

     首先b节点本身的频次符合minSupport，所以是一个频繁项(b : 5)，然后b节点往上找subTree，只有跟节点，所以解锁，b为前缀的频繁项只有一个：（b : 5）。

2、商品a频繁项的挖掘

    显然a本身是个频繁项(a : 3)，然后递归的获取a的子树，进行挖掘。

子树构建方式如下：新建一个新的FP树，然后遍历树中所有的a节点，往上找，直到root节点，然后把当前路径上的非根节点添加到subTree中，每个节点的频次为当前遍历节点的频次。

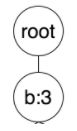
因为a只有一个节点(a, 3)，所以往上遍历得到节点b，因此把b加入subTree中，频次为节点(a, 3)的频次3。得到如下subTree，显然在这个subTree中只能挖掘出频繁项(b : 3)，然后别忘了这是a递归得到的子树，得拼上前缀a，所以得到频繁项为(ab : 3)

 

 

3、商品c频繁项的挖掘

    商品c在FP树中包含两个节点，分别为: (c, 1), (c, 2)。显然c自身是个频繁项(c : 3)，然后进行递归。(c, 1)节点往上路径得到如下节点：(a, 1), (b, 1)。节点(c, 2)往上得到(b, 2)，subTree中的节点(b, 3)符合minsupport,拼上前缀c得到频繁项(cb : 3)。节点(c, 1)不满足要求，丢弃。

上述三个节点可以构造出如下的subTree:

 

 

4、商品d频繁项的挖掘

    子树首先挖出(c : 2)，(b : 3)，拼上前缀d得到(dc : 2),(db : 3)，然后subTree中的节点c的subTree仅仅有根节点和节点(b, 2)，拼上两个前缀得到(dcb : 2)。

 

spark java 代码：

import java.io.Serializable;
public class Item implements Serializable {
	  private String[] items;

	  public Item(String[] a){
		  this.items=a;
	  }
	public String[] getItems() {
		return items;
	}
	public void setItems(String[] items) {
		this.items = items;
	}			 
}


import org.apache.spark.ml.fpm.*;
import org.apache.spark.ml.param.Param;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Encoder;
import org.apache.spark.sql.Encoders;
import org.apache.spark.sql.SparkSession;
import java.util.Arrays;
import org.apache.spark.SparkConf;

public class Test01 {
	public static void main(String[] args) {
    SparkConf spconf=new  SparkConf().setMaster("local[4]").setAppName("testFGGrowth");
    SparkSession spsession=SparkSession.builder().config(spconf).getOrCreate();
    
   String[] str1 = {"a", "b", "d"};
   String[] str2 = {"b", "c", "d"};
   String[] str3 = {"a", "b", "e"};
   String[] str4 = {"a", "b", "c"};
   String[] str5 = {"b", "c", "d"};
 Item item1 = new Item(str1);
 Item item2 = new Item(str2);
 Item item3 = new Item(str3);
 Item item4 = new Item(str4);
 Item item5 = new Item(str5);  
  Encoder itemEncoder = Encoders.bean(Item.class);
  Dataset ds=spsession.createDataset(Arrays.asList(item1,item2,item3,item4,item5),itemEncoder);
  ds.show();
  FPGrowth fpGrowth=new FPGrowth().setMinSupport(0.2).setMinConfidence(0.4).setNumPartitions(3);
   fpGrowth.setItemsCol("items");
   FPGrowthModel model= fpGrowth.fit(ds);
   Param colParam=fpGrowth.itemsCol();
   Dataset freqItems=model.freqItemsets();
   freqItems.show();
   Dataset assoRule= model.associationRules();
   assoRule.show();
	}
}
结果：
1）频繁集
+---------+----+
|    items|freq|
+---------+----+
|      [a]|   3|
|   [a, d]|   1|
|[a, d, b]|   1|
|   [a, c]|   1|
|[a, c, b]|   1|
|   [a, b]|   3|
|      [b]|   5|
|      [e]|   1|
|   [e, a]|   1|
|[e, a, b]|   1|
|   [e, b]|   1|
|      [c]|   3|
|   [c, b]|   3|
|      [d]|   3|
|   [d, c]|   2|
|[d, c, b]|   2|
|   [d, b]|   3|
+---------+----+
关联规则：
+----------+----------+------------------+------------------+
|antecedent|consequent|        confidence|              lift|
+----------+----------+------------------+------------------+
|       [b]|       [a]|               0.6|               1.0|
|       [b]|       [c]|               0.6|               1.0|
|       [b]|       [d]|               0.6|               1.0|
|    [e, a]|       [b]|               1.0|               1.0|
|       [a]|       [b]|               1.0|               1.0|
|       [c]|       [b]|               1.0|               1.0|
|       [c]|       [d]|0.6666666666666666|1.1111111111111112|
|    [d, c]|       [b]|               1.0|               1.0|
|       [d]|       [c]|0.6666666666666666|1.1111111111111112|
|       [d]|       [b]|               1.0|               1.0|
|    [c, b]|       [d]|0.6666666666666666|1.1111111111111112|
|    [d, b]|       [c]|0.6666666666666666|1.1111111111111112|
|       [e]|       [a]|               1.0|1.6666666666666667|
|       [e]|       [b]|               1.0|               1.0|
|    [e, b]|       [a]|               1.0|1.6666666666666667|
|    [a, d]|       [b]|               1.0|               1.0|
|    [a, c]|       [b]|               1.0|               1.0|
+----------+----------+------------------+------------------+