一种无需预先指定聚类个数的算法——Dbscan聚类算法

一、DBSCAN算法

1、介绍

1、算法介绍

  在之前我们介绍了两种聚类算法，分别是模糊C均值聚类和K均值聚类。这两种算法都要求我们提前给定聚类的个数。而且这些基于距离的聚类算法的聚类结果是球状的簇，当数据集中的聚类结果是非球状结构时，基于距离的聚类算法的聚类效果并不好。今天我们就来介绍一种无需预先指定聚类个数的算法——Dbscan聚类算法
  DBSCAN(Density-based spatial clustering of applications with noise)是Martin Ester,Hans-PeterKriegel等人于1996年提出的一种基于密度的聚类方法，聚类前不需要预先指定聚类的个数,生成的簇的个数不定(和数据有关)。该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象)的数目不小于某一给定阈值。该方法能在具有噪声的空间数库中发现任意形状的簇，可将密度足够大的相邻区域连接,能有效处理异常数据。

  

“谁离我挨得近，我就是谁兄弟。兄弟的兄弟也就是我的兄弟”

2、算法原理

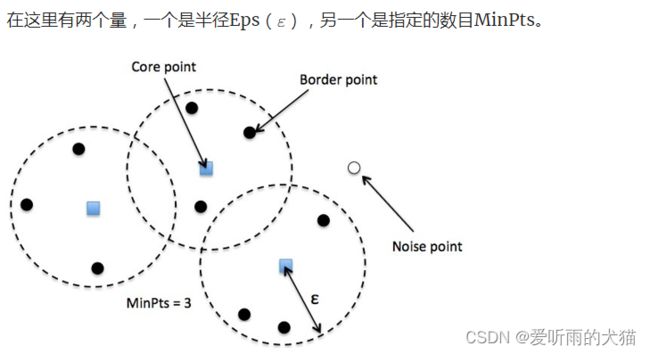
  在DBSCAN算法中将数据点分为三类:

• 核心点( Core point)。若样本$x_i$的$ϵ$邻域内至少包含了$MinPts$个样本,即$N_{ϵ}(X_i)>MinPts$,则称样本点$x_i$为核心点。
• 边界点(Border point)。若样本$x_i$的$ϵ$邻域包含的样本数目小于$MinPts$，但是它在其他核心点的邻域内,则称样本点$x_i$为边界点。
• 噪音点(Noise)。既不是核心点也不是边界点的点
  
• 密度直达(directly density-reachable) :我们称样本点$p$是由样本点$q$对于参数{$Eps,MinPts$}密度直达的，如果它们满足$p\in NEps(q)$且$|NEps(q)|\ge MinPts$(即样本点$q$是核心点)
• 密度可达(density-reachable) :我们称样本点$p$是由样本点$q$对于参数{$Eps,MinPts$}密度可达的，如果存在一系列的样本点$p_1,..,p_n$ (其中$p_1=q,p_n=p$)使得对于i=1,$.,n-1$,样本点$p_{i+1}$可由样本点$p_i$密度直达
• 密度相连(density-connected):我们称样本点$p$与样本点$q$对于参数{$Eps,MinPts$} 是密度相连的，如果存在一个样本点$o$，使得$p$和$q$均由样本点$o$密度可达。
  
    从上图可以很容易看出理解上述定义,图中$MinPts=5$,红色的点都是核心对象,因为其$ϵ$-邻域至少有5个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内,如果不在超球体内,则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的$ϵ$-邻域内所有的样本相互都是密度相连的。

3、算法步骤

• 首选任意选取一个点,然后找到到这个点距离小于等于$Eps$的所有的点。如果距起始点的距离在$Eps$之内的数据点个数小于$MinPts$，那么这个点被标记为噪声。如果距离在$Eps$之内的数据点个数大于$MinPts$，则这个点被标记为核心样本,并被分配一个新的簇标签。
• 然后访问该点的所有邻居(在距离$Eps$以内)。如果它们还没有被分配一个簇,那么就将刚刚创建的新的簇标签分配给它们。如果它们是核心样本,那么就依次访问其邻居,以此类推。簇逐渐增大,直到在簇的$Eps$距离内没有更多的核心样木为止。
• 选取另一个尚未被访问过的点,并重复相同的过程。

  如下图所示：
  在这幅图里, $MinPts$=4,点A和其他红色点是核心点,因为它们的$ϵ$-邻域(图中红色圆圈)里包含最少4个点(包括自己)，由于它们之间相互相可达，它们形成了一个聚类。点B和点C不是核心点，但它们可由A经其他核心点可达，所以也属于同一个聚类。点N是局外点，它既不是核心点，又不由其他点可达。

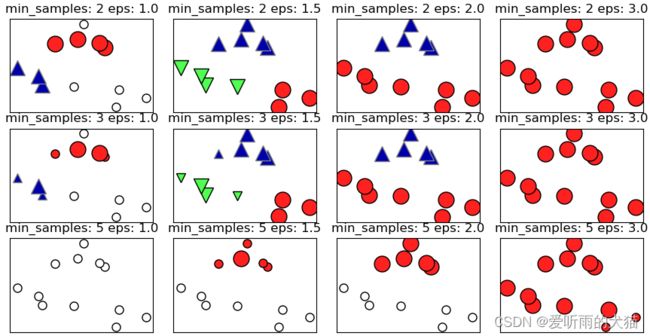
3、参数选择

• $Eps$设置得非常小,则意味着没有点是核心样本,可能会导致所有点被标记为噪声
• $Eps$设置得非常大,可能会导致所有点形成单个簇。
• 虽然不需要显示设置簇的个数,但设置$Eps$可以隐式地控制找到eps的个数。
  

4、Dbscan可视化

 

Dbscan可视化
  Dbscan可视化 (https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/)。
  当我们选择不同的epsilon和minPoints时，将会呈现不同的效果。大家也可以尝试一下其他的图形。
  视频如下图展示：

  视频展示(https://v.youku.com/v_show/id_XNTg5MzUzMTQ0OA==.html。
  密码：1234

2、MATLAB实现

  下面我们举个小例子来使用该函数进行聚类：
  1)、在1至500的正方形网格点上随机生成3000个点，使用x和y表示这3000个点的横纵坐标。

clc;
clear;
rng(100)%随机数种子
idx = randperm(500^2,3000);
[x,y] = ind2sub([500,500],idx);
x = x';y = y';

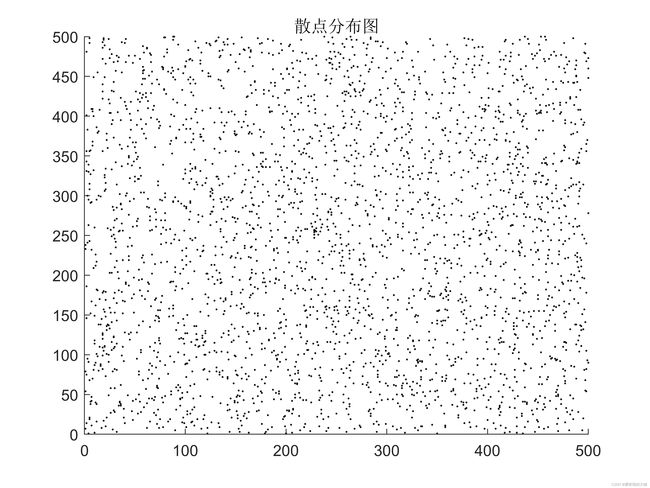
  2)、画出这3000个点的散点图

figure(1);
scatter(x,y,0.5,'k')%0.5表示散点大小
title('散点分布图')
axis([0,500,0,500])%设置x轴和y轴范围

  效果如下图所示：

  3)、对这三千个点进行聚类，规则如下：将距离小于10的点聚成一类，例如A和B距离为8，则将A和B聚类一类，且该聚类具有传递性，假设C和B的距离为5.21，则C也和A、B归于同一类。

epsilon = 10;%半径
minpts = 1;%只要包含一个点就可以认为一类，即不含噪声点
idx = dbscan([x,y],epsilon,minpts);
length(unique(idx))%聚类的类别数
[gc,grps] = groupcounts(idx);%gc 每一类含有的样本数，grps 分成的类别

  从结果可以看出一共被分为了211类。idx保存了聚类的结果，数值相同即被分在了同一类。gc保存了每一类含有的样本数，grps保存了分成的类别。例如gc(1) = 26，表示第一类含有23个点
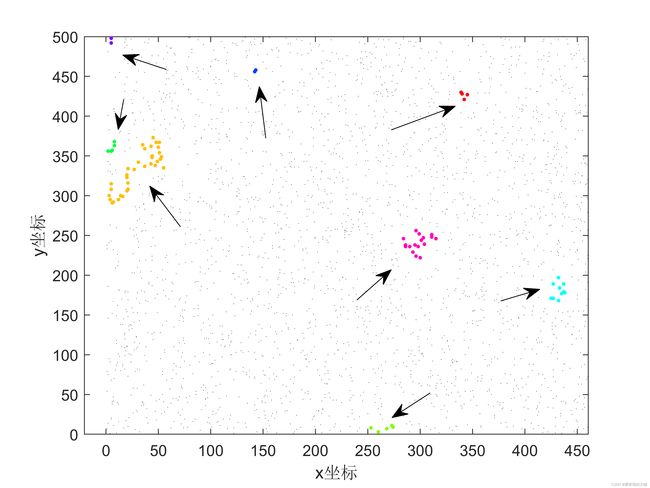
  4)、对聚类结果可视化

figure(2)
gscatter(x,y,idx,[],[],1,'doleg','off');
xlabel('x坐标');ylabel('y坐标');

  可视化结果如下所示：

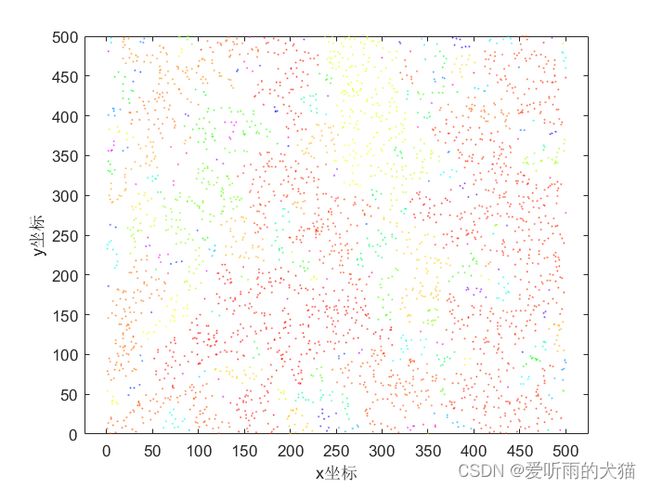
  这里我们用到了gcatter函数，它能根据分类结果来绘制散点图，但要注意的是，由于我们的类别太多，MATLAB内置的颜色不足，因此可能有某些不同的类别使用的颜色也相同，因此下面我们可以考虑：每次随机的取出k个类别画图，将其他的类别全部绘制为黑色：
  5)、每次随机的取出k个类别画图，将其他的类别全部绘制为黑色

k = 5;
p = randperm(length((unique(idx))),k);
[id1,pp] = ismember(idx,p);   id0 = ~id1;
x1 = x(id1); y1 = y(id1);   % 作者：数学建模清风
x0 = x(id0); y0 = y(id0); 
figure('Name',"随机显示"+k+"个类别的效果图",'NumberTitle','off');
gscatter(x1,y1,pp(pp~=0),[],'.',8,'doleg','off')
hold on 
scatter(x0,y0,1,'.k')
hold off
xlabel('x坐标'); ylabel('y坐标')

  结果如下所示：

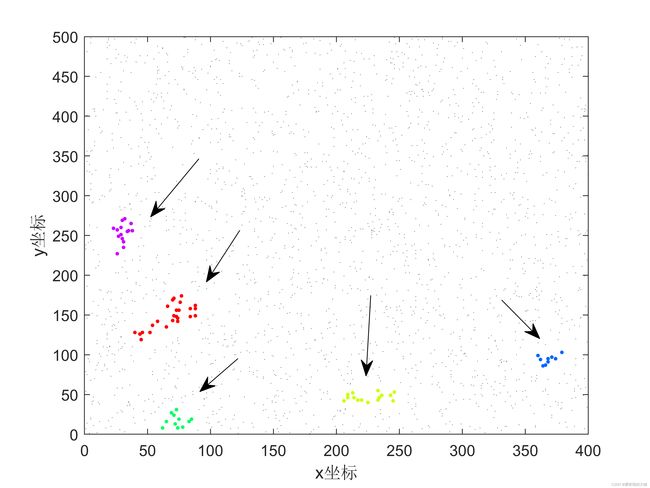
  注意，这是随机取的k个类别（上图k等于5），因此每次运行的结果可能也不同，下图是k取8时随机生成的一个图形，大家也可以自己测试完成。

  5)、全部代码：

%% 导入数据并显示
clc;
clear;
rng(100)%随机数种子
idx = randperm(500^2,3000);
[x,y] = ind2sub([500,500],idx);
x = x';y = y';

figure(1);
scatter(x,y,0.5,'k')%0.5表示散点大小
title('散点分布图')
axis([0,500,0,500])%设置x轴和y轴范围
%% 进行Dbscan聚类
epsilon = 10;%半径
minpts = 1;%只要包含一个点就可以认为一类，即不含噪声点
idx = dbscan([x,y],epsilon,minpts);
length(unique(idx))%聚类的类别数
[gc,grps] = groupcounts(idx);%gc 每一类含有的样本数，grps 分成的类别
%% 画聚类后的图
figure(2)
gscatter(x,y,idx,[],[],1.5,'doleg','off');
xlabel('x坐标');ylabel('y坐标');
%% 每次显示5个簇
k = 5;
p = randperm(length((unique(idx))),k);
[id1,pp] = ismember(idx,p);   id0 = ~id1;
x1 = x(id1); y1 = y(id1);   % 作者：数学建模清风
x0 = x(id0); y0 = y(id0); 
figure('Name',"随机显示"+k+"个类别的效果图",'NumberTitle','off');
gscatter(x1,y1,pp(pp~=0),[],'.',8,'doleg','off')
hold on 
scatter(x0,y0,1,'.k')
hold off
xlabel('x坐标'); ylabel('y坐标')

  
  
  
  

喜欢的小伙伴麻烦点个赞奥，谢谢啦

参考：
https://zh.wikipedia.org/wiki/DBSCAN
https://www.biaodianfu.com/dbscan.html
https://www.imooc.com/article/257210
数学建模清风