python神经网络编程 豆瓣,小波神经网络预测python

什么是“小波神经网络”？能干什么用呀

小波神经网络（Wavelet Neural Network， WNN）是在小波分析研究获得突破的基础上提出的一种人工神经网络。

它是基于小波分析理论以及小波变换所构造的一种分层的、多分辨率的新型人工神经网络模型。 即用非线性小波基取代了通常的非线性Sigmoid 函数，其信号表述是通过将所选取的小波基进行线性叠加来表现的。

它避免了BP 神经网络结构设计的盲目性和局部最优等非线性优化问题，大大简化了训练，具有较强的函数学习能力和推广能力及广阔的应用前景。

“小波神经网络”的应用：1、在影像处理方面，可以用于影像压缩、分类、识别与诊断，去污等。在医学成像方面的减少B超、CT、核磁共振成像的时间，提高解析度等。2、在信号分析中的应用也十分广泛。

它可以用于边界的处理与滤波、时频分析、信噪分离与提取弱信号、求分形指数、信号的识别与诊断以及多尺度边缘侦测等。3、在工程技术等方面的应用。

包括电脑视觉、电脑图形学、曲线设计、湍流、远端宇宙的研究与生物医学方面。扩展资料：小波神经网络这方面的早期工作大约开始于1992 年，主要研究者是Zhang Q、Harold H S 和焦李成等。

其中，焦李成在其代表作《神经网络的应用与实现》中从理论上对小波神经网络进行了较为详细的论述。近年来，人们在小波神经网络的理论和应用方面都开展了不少研究工作。

小波神经网络具有以下特点：首先，小波基元及整个网络结构的确定有可靠的理论根据，可避免BP 神经网络等结构设计上的盲目性；其次，网络权系数线性分布和学习目标函数的凸性，使网络训练过程从根本上避免了局部最优等非线性优化问题；第三，有较强的函数学习能力和推广能力。

小波神经网络的优势是什么？谢谢

小波神经网络相比于前向的神经网络,它有明显的优点:首先小波神经网络的基元和整个结构是依据小波分析理论确定的,可以避免BP神经网络等结构设计上的盲目性;其次小波神经网络有更强的学习能力,精度更高AI爱发猫 www.aifamao.com。

总的而言，对同样的学习任务,小波神经网络结构更简单,收敛速度更快，精度更高。

Hopfield神经网络用python实现讲解？

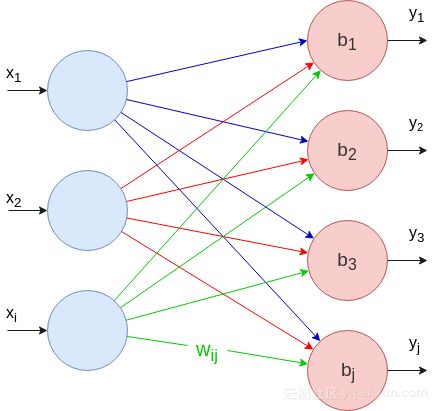
神经网络结构具有以下三个特点：神经元之间全连接，并且为单层神经网络。每个神经元既是输入又是输出，导致得到的权重矩阵相对称，故可节约计算量。

在输入的激励下，其输出会产生不断的状态变化，这个反馈过程会一直反复进行。

假如Hopfield神经网络是一个收敛的稳定网络，则这个反馈与迭代的计算过程所产生的变化越来越小，一旦达到了稳定的平衡状态，Hopfield网络就会输出一个稳定的恒值。

Hopfield网络可以储存一组平衡点，使得当给定网络一组初始状态时，网络通过自行运行而最终收敛于这个设计的平衡点上。

当然，根据热力学上，平衡状态分为stablestate和metastablestate,这两种状态在网络的收敛过程中都是非常可能的。为递归型网络，t时刻的状态与t-1时刻的输出状态有关。

之后的神经元更新过程也采用的是异步更新法(Asynchronous)。Hopfield神经网络用python实现。

如何用9行Python代码编写一个简易神经网络

学习人工智能时，我给自己定了一个目标－－用Python写一个简单的神经网络。为了确保真得理解它，我要求自己不使用任何神经网络库，从头写起。多亏了AndrewTrask写得一篇精彩的博客，我做到了！

下面贴出那九行代码：在这篇文章中，我将解释我是如何做得，以便你可以写出你自己的。我将会提供一个长点的但是更完美的源代码。首先，神经网络是什么？人脑由几千亿由突触相互连接的细胞（神经元）组成。

突触传入足够的兴奋就会引起神经元的兴奋。这个过程被称为“思考”。我们可以在计算机上写一个神经网络来模拟这个过程。不需要在生物分子水平模拟人脑，只需模拟更高层级的规则。

我们使用矩阵（二维数据表格）这一数学工具，并且为了简单明了，只模拟一个有3个输入和一个输出的神经元。我们将训练神经元解决下面的问题。前四个例子被称作训练集。你发现规律了吗？‘？’是0还是1？

你可能发现了，输出总是等于输入中最左列的值。所以‘？’应该是1。训练过程但是如何使我们的神经元回答正确呢？赋予每个输入一个权重，可以是一个正的或负的数字。

拥有较大正（或负）权重的输入将决定神经元的输出。首先设置每个权重的初始值为一个随机数字，然后开始训练过程：取一个训练样本的输入，使用权重调整它们，通过一个特殊的公式计算神经元的输出。

计算误差，即神经元的输出与训练样本中的期待输出之间的差值。根据误差略微地调整权重。重复这个过程1万次。最终权重将会变为符合训练集的一个最优解。

如果使用神经元考虑这种规律的一个新情形，它将会给出一个很棒的预测。这个过程就是backpropagation。计算神经元输出的公式你可能会想，计算神经元输出的公式是什么？

首先，计算神经元输入的加权和，即接着使之规范化，结果在0，1之间。为此使用一个数学函数－－Sigmoid函数：Sigmoid函数的图形是一条“S”状的曲线。

把第一个方程代入第二个，计算神经元输出的最终公式为：你可能注意到了，为了简单，我们没有引入最低兴奋阈值。调整权重的公式我们在训练时不断调整权重。但是怎么调整呢？

可以使用“ErrorWeightedDerivative”公式：为什么使用这个公式？首先，我们想使调整和误差的大小成比例。其次，乘以输入（0或1），如果输入是0，权重就不会调整。

最后，乘以Sigmoid曲线的斜率（图4）。

为了理解最后一条，考虑这些：我们使用Sigmoid曲线计算神经元的输出如果输出是一个大的正（或负）数，这意味着神经元采用这种（或另一种）方式从图四可以看出，在较大数值处，Sigmoid曲线斜率小如果神经元认为当前权重是正确的，就不会对它进行很大调整。

乘以Sigmoid曲线斜率便可以实现这一点Sigmoid曲线的斜率可以通过求导得到：把第二个等式代入第一个等式里，得到调整权重的最终公式：当然有其他公式，它们可以使神经元学习得更快，但是这个公式的优点是非常简单。

构造Python代码虽然我们没有使用神经网络库，但是将导入Python数学库numpy里的4个方法。

分别是：exp－－自然指数array－－创建矩阵dot－－进行矩阵乘法random－－产生随机数比如，我们可以使用array()方法表示前面展示的训练集：“.T”方法用于矩阵转置（行变列）。

所以，计算机这样存储数字：我觉得我们可以开始构建更优美的源代码了。给出这个源代码后，我会做一个总结。我对每一行源代码都添加了注释来解释所有内容。注意在每次迭代时，我们同时处理所有训练集数据。

所以变量都是矩阵（二维数据表格）。下面是一个用Python写地完整的示例代码。我们做到了！我们用Python构建了一个简单的神经网络！首先神经网络对自己赋予随机权重，然后使用训练集训练自己。

接着，它考虑一种新的情形[1,0,0]并且预测了0.99993704。正确答案是1。非常接近！传统计算机程序通常不会学习。

而神经网络却能自己学习，适应并对新情形做出反应，这是多么神奇，就像人类一样。

小波神经网络比一般神经网络的优势是什么？

关于Python的BP神经网络的一个代码 100