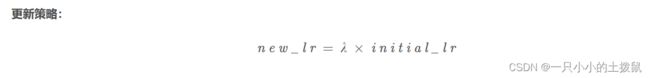pytorch----深度学习中学习率的衰减策略

1、为什么要调整学习率

神经网络 参数更新的机制是-梯度下降+反向传播，将输出误差 反向传播 给网络参数，以此来拟合样本的输出。本质上是最优化的一个过程，逐步趋向于最优解。但是每一次更新参数利用多少误差，就需要通过一个参数来控制，这个参数就是学习率（Learning rate）,也称为步长。

学习率是 神经网络 优化时的重要超参数。学习率α的取值非常关键，学习率越大则权重更新的越快。在梯度下降方法中，如果过大就不会收敛，如果过小则收敛速度太慢。学习率越大，输出误差对参数的影响就越大，参数更新的就越快，但同时受到异常数据的影响也就越大，很容易发散。

一般来说，我们希望在训练初期学习率大一些，使得网络收敛迅速，在训练后期学习率小一些，使得网络在收敛到最优点附近时避免来回震荡，从而更好的收敛到最优解。 因此，比较简单直接的学习率调整可以通过学习率衰减（Learning Rate Decay）的方式来实现。

	学习率大	学习率小
学习速度	快	慢
使用时间点	刚开始训练时（收敛迅速）	一定轮数后（不易振荡）
缺点	1、易损失值爆炸 2、易振荡	1、易过拟合 2、收敛速度慢

在训练过程中，参数更新向着 损失函数 梯度下降的方向

                                                      

 其中  ：是梯度，就是损失函数loss的导数

 2、学习率衰减机制

可以看出，最理想的学习率不是固定值，而是一个随着训练次数衰减的变化的值，也就是在训练初期，学习率比较大，随着训练的进行，学习率不断减小，直到模型收敛。

常用的衰减机制有： 固定策略的学习率衰减和自适应学习率衰减，其中固定学习率衰减包括分段衰减、逆时衰减、指数衰减等，自适应学习率衰减包括AdaGrad、 RMSprop、 AdaDelta等，可以针对每个参数设置不同的学习率。一般情况，两种策略会结合使用。本文用到的代码

learning_all = []  # 存放损失的数组
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
#scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.96)#指数衰减
#scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.65)#固定步长衰减
#scheduler=torch.optim.lr_scheduler.MultiStepLR(optimizer,milestones=[50, 55, 65, 75, 80], gamma=0.8)#多步步长衰减
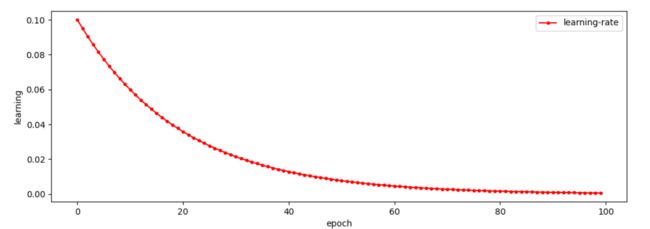
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=80, eta_min=0.0000001)#余弦衰减
#scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min',factor=0.999, patience=10,verbose=True, threshold=0.0001, threshold_mode='rel',cooldown=0, min_lr=0, eps=1e-08)
#lambda2 = lambda epoch: 0.95 ** epoch
#scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda2], last_epoch=-1)
for epoch in range(100):
#adjust_learning_rate(optimizer, epoch)
     a=random.uniform(0.1,0.05)
     aa.append(a)
     scheduler.step()
     scheduler1.step()
     scheduler2.step(a)
     for param_group in optimizer.param_groups:
        learning_all.append(param_group['lr'])
        print(param_group['lr'])
plt.figure(figsize=(12, 4))
plt.plot(range(100), learning_all,"r.-", label="learning-rate")
plt.xlabel("epoch")
plt.ylabel("learning")
plt.legend()
plt.show()

    optimizer.defaults： 字典，存放这个优化器的一些初始参数，有： 'lr', 'betas', 'eps', 'weight_decay', 'amsgrad'。事实上这个属性继承自 torch.optim.Optimizer父类；
    optimizer.param_groups：列表，每个元素都是一个字典，每个元素包含的关键字有： 'params', 'lr', 'betas', 'eps', 'weight_decay', 'amsgrad'， params类是各个网络的参数放在了一起。这个属性也继承自 torch.optim.Optimizer父类。

由于上述两个属性都继承自所有优化器共同的基类，所以是所有优化器类都有的属性，并且两者字典中键名相同的元素值也相同（经过lr_scheduler后 lr就不同了）。

 lr_scheduler调整方法:根据epochs

该方法中提供了多种基于epoch训练次数进行学习率调整的方法。

（1）指数衰减

学习率按照指数的形式衰减是比较常用的策略，也是最有效的。首先要确定针对哪个优化器，执行学习率动态调整策略，先定义一个优化器，然后给这个优化器绑定一个指数衰减学习率控制器：

#定义优化器
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
#指数衰减学习率控制器： 即每个epoch都衰减lr = lr * gamma,即进行指数衰减
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.96)

其中 参数gamma表示衰减的底数，选择不同的gamma值可以获得幅度不同的衰减曲线

0.1 > 0.096 > 0.09215 > 0.08847 > 0.0849 > 0.0815 > 0.0782.........

（2） 分段衰减

有时希望学习率每个一定步长（或者epoch）就衰减为原来的gamma分之一，即按照固定的区间长度进行学习率更新，或者希望不同的区间采用不同的更新频率，有的区间更新学习率，有的区间不更新学习率 ，使用时依旧先定义优化器，在给优化器绑定StepLR或者MultiStepLR控制器来实现区间长度控制：

#即在规定步长都衰减lr = lr * gamma,进行衰减
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
#固定步长衰减，gamma参数表示衰减的程度，step_size参数表示每隔多少个step进行一次学习率调整
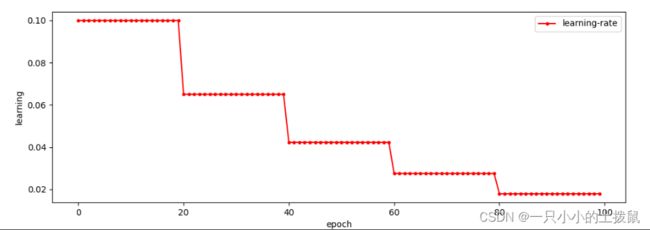
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.65)
#多步长衰减 ，gamma参数表示衰减的程度，，milestones参数为表示学习率更新的起止区间，
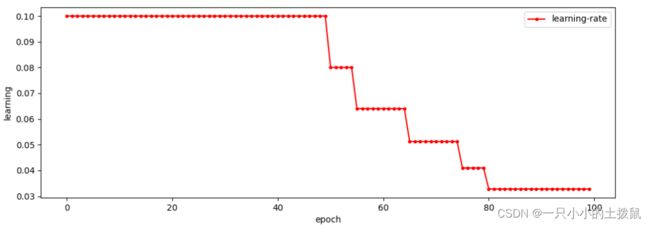
scheduler=torch.optim.lr_scheduler.MultiStepLR(optimizer,
                            milestones=[50, 55, 65, 75, 80], gamma=0.8)

0.1 >...0.065> ...0.04225...> ...0.02746> ....01785

 

 

从图中可以看出，学习率在区间[50， 80]内快速的下降，这就是milestones参数所控制的，在milestones以外的区间学习率始终保持不变。

 （3）余弦退火衰减

它使得学习率按照周期变化，其包含的参数和余弦知识一样，参数T_max表示余弦周期；eta_min表示学习率的最小值，默认它是0表示学习率至少为正值。确定一个余弦函数需要知道最值和周期，其中周期就是T_max，最值是初始学习率。其定义方式如下：

optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
#
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=80,                     
                            eta_min=0.0000001)

 0.1> 0.0999> 0.0998> 0.0996> 0.0993> 0.0990>0.0986....

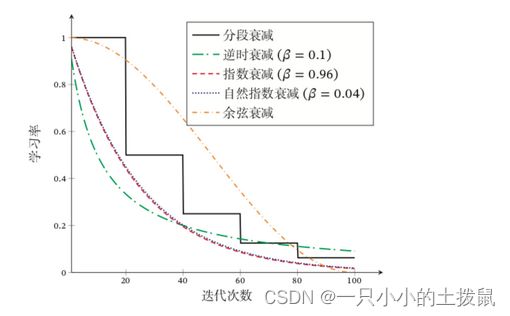
 下图给出了不同衰减方法的示例（假设初始学习率为 1）。

 

lr_scheduler调整方法:根据测试指标自适应调整

当网络的 评价指标 不在提升的时候，例如，当验证集的 loss 不再下降时，进行学习率调整；或者监测验证集的 accuracy，当accuracy 不再上升时，则调整学习率。可以通过降低网络的学习率来提高网络性能。

所使用的类 torch.optim.lr_scheduler.ReduceLROnPlateau，该方法提供了一些基于训练过程中的某些测量值对学习率进行动态的下降。使用的时候需要选择网络的度量指标(test_loss)，括号中就是指标一般用验证集的loss。 使用如下类的step方法实现

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
scheduler = ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10,
                                verbose=False, threshold=0.0001, threshold_mode='rel', 
                                    cooldown=0, min_lr=0, eps=1e-08)
.....
scheduler.step(train_loss)

•  optimer指的是网络的优化器
• mode (str) ，可选择‘min’或者‘max’，min表示当监控量停止下降的时候(如监测loss)，学习率将减小，max表示当监控量停止上升的时候(如监测 accuracy)，学习率将减小。默认值为‘min’
• factor 学习率每次降低多少比例，new_lr = old_lr * factor
• patience=10，容忍网路的性能不提升的次数，高于这个次数就降低学习率，当指标连续patience次数还没有改进时，降低学习率。
• verbose（bool） - 如果为True，则为每次更新向stdout输出一条消息。 默认值：False
• threshold（float） - 测量新最佳值的阈值，仅关注重大变化。 默认值：1e-4
• cooldown： 当调整学习率之后，让学习率调整策略冷静一下，让模型再训练一段时间，再重启监测模式。默认值：0。
• min_lr,学习率的下限，可为 float，或者 list，当有多个参数组时，可用 list 进行设置。
• eps ，适用于lr的最小衰减。 如果新旧lr之间的差异小于eps，则不调整学习率。。 默认值：1e-8。

（1）自适应学习率

Adagrad算法：在Adagrad算法中，如果某个参数的偏导数累积比较大，其学习率相对较小；相反，如果其偏导数累积较小，其学习率相对较大。但整体是随着迭代次数的增加，学习率逐渐缩小。Adagrad算法的缺点是在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点。

RMSprop算法：RMSprop算法是Geoff Hinton提出的一种自适应学习率的方法[Tieleman and Hinton, 2012]，可以在有些情况下避免AdaGrad算法中学习率不断单调下降以至于过早衰减的缺点。RMSProp算法和Adagrad算法的区别在于G t 的计算由累积方式变成了指数衰减移动平均。在迭代过程中，每个参数的学习率并不是呈衰减趋势，既可以变小也可以变大。

AdaDelta算法：AdaDelta算法[Zeiler, 2012]也是 Adagrad算法的一个改进。和RMSprop算法类似，AdaDelta算法通过梯度平方的指数衰减移动平均来调整学习率。此外，AdaDelta算法还引入了每次参数更新差∆θ的平方的指数衰减权移动平均。

 lr_scheduler调整方法:自定义调整

 lr_lambda(function or list)- 一个计算学习率调整倍数的函数，输入通常为 step，当有多个参数组时，设为 list。LambdaLR更新学习率方式是：

 # Assuming optimizer has two groups.
 lambda1 = lambda epoch: epoch // 30
 lambda2 = lambda epoch: 0.95 ** epoch
 scheduler = LambdaLR(optimizer, lr_lambda=[lambda2], last_epoch=-1)
 for epoch in range(100):
     scheduler.step()
     train(...)
     validate(...)

• optimizer:封装好的优化器。
• lr_lambda( function or list):一个计算每个epoch的学习率的函数或者一个list，当是一个函数时，需要给其一个整数参数，使其计算出一个乘数因子，用于调整学习率，通常该输入参数是epoch数目或者是一组上面的函数组成的列表。
• last_epoch:最后一个epoch的索引 。

0.1 > 0.095> 0.09025> 0.0857375> 0.081450625......

3、在模型中的使用

torch.optim.lr_scheduler模块提供了一些根据epoch训练次数来调整学习率（learning rate）的方法。一般情况下我们会设置随着epoch的增大而逐渐减小学习率从而达到更好的训练效果。
而 torch.optim.lr_scheduler.ReduceLROnPlateau则提供了基于训练中某些测量值使学习率动态下降的方法。

这些负责学习率调整的类，其完整对学习率的更新都是在其step()函数被调用以后完成的，这个step表达的含义可以是一次迭代，当然更多情况下应该是一个epoch以后进行一次scheduler.step()，这根据具体问题来确定。scheduler.step()函数的调用应该放在optimizer更新之后：

scheduler = ...
>>> for epoch in range(100):
>>>     train(...)
>>>     validate(...)
>>>     scheduler.step()

学习率衰减策略很大程度上是 依赖于经验与具体问题的 ，不能照搬参数。 指数衰减学习率是深度学习调参过程中比较使用的一个方法， 刚开始训练时，学习率以 0.01 ~ 0.001 为宜， 接近训练结束的时候，学习速率的衰减应该在100倍以上 。按照这个经验去设置相关参数，对于模型的精度会有很大帮助。

参考文献：深度神经网络的优化算法 - 走看看

 几种学习率衰减策略_南苏月的博客-CSDN博客_学习率衰减

PyTorch学习之六个学习率调整策略_mingo_敏的博客-CSDN博客_pytorch 学习率

torch.optim — PyTorch 1.11.0 documentation

 torch.optim.lr_scheduler：调整学习率_qyhaill的博客-CSDN博客_lr_scheduler