Faster RCNN 中的RPN解析

Faster RCNN 中的RPN解析

RCNN和Fast RCNN中使用Selective Search方法找出所有的候选框，SS方法非常耗时。Faster RCNN中提出RPN(region proposal network)替代SS方法提取候选框，并提出anchor的概念。虽然目前anchor free的各种算法层出不穷，但是anchor的思想也曾引领风潮。

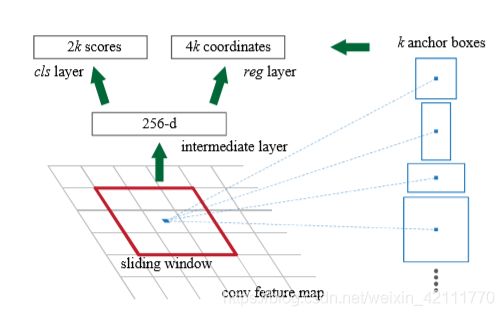
RPN是一个轻量级的网络，仅仅包含一个33的卷积，11的分类层和1*1的回归层。RPN中引入了anchor的概念，每一个anchor要分positive和negative标签，所以分类分支将有2k个输出，每个anchor以$\left(x,y,w,h\right)$表示坐标位置，回归分支将有4k个输出。

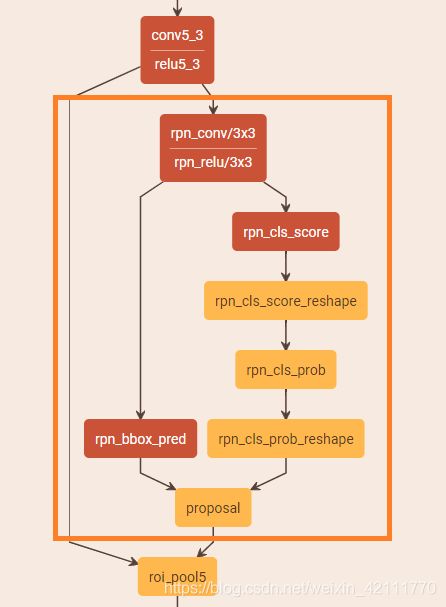
下图来自于py-faster-rcnn/models/pascal_voc/VGG16/faster_rcnn_end2end/test.prototxt中的RPN部分。

Anchor

RPN网络简单，但是刚入门时，有些不好理解，其中最难的地方在于anchor。anchor介绍见Faster RCNN中的Anchor

分类

在分类分支，由于anchor有背景和前景(bg/fg)之分，所有输出channels为2* 9=18，按照caffe的blob的格式，rpn_cls_score的输出格式为[batchsize, 18, H, W]。做softmax计算时，当axis=1，且预测大小为 (N, C, H, W)时，要求labels的数量为NHW。

分析：假设conv5_3的特征图形状为[N, C, H, W]，经过一个33滑动窗口之后，输出大小为[N, 256, H, W]，后又接一个11卷积的分类层，输出大小为[N, 2k, H, W]。对于大小为[H, W]的特征图，其生成的anchors数量为$H\ast W\ast k$，所以总label 数量为HW*k。因此softmax运算时需要reshape一些，后再reshape恢复原状。

layer {
  name: "rpn_cls_score"
  type: "Convolution"
  bottom: "rpn/output"
  top: "rpn_cls_score"
  param { lr_mult: 1.0 decay_mult: 1.0 }
  param { lr_mult: 2.0 decay_mult: 0 }
  convolution_param {
    num_output: 18   # 2(bg/fg) * 9(anchors)
    kernel_size: 1 pad: 0 stride: 1
    weight_filler { type: "gaussian" std: 0.01 }
    bias_filler { type: "constant" value: 0 }
  }
}
layer {
   bottom: "rpn_cls_score"
   top: "rpn_cls_score_reshape"
   name: "rpn_cls_score_reshape"
   type: "Reshape"
   reshape_param { shape { dim: 0 dim: 2 dim: -1 dim: 0 } }
}
layer {
  name: "rpn_cls_prob"
  type: "Softmax"
  bottom: "rpn_cls_score_reshape"
  top: "rpn_cls_prob"
}
layer {
  name: 'rpn_cls_prob_reshape'
  type: 'Reshape'
  bottom: 'rpn_cls_prob'
  top: 'rpn_cls_prob_reshape'
  reshape_param { shape { dim: 0 dim: 18 dim: -1 dim: 0 } }
}

bounding box regression

bboxes通常以四维向量$\left(x,y,w,h\right)$表示，$\left(x,y\right)$是一个bbox的中心点坐标，$\left(w,h\right)$为一个bbox的宽和高。如上图所示，假设红色矩形$P$为Proposal box，绿色的框$G$为ground-truth box。那么我们希望$P$能够经过函数映射得到一个和$G$更接近的回归框框$\hat{G}$，如上图蓝色矩形。

用数学公式描述就是：给定$\left(P_x,P_y,P_w,P_h\right)$，寻找一映射$f$，使得$f\left(P_x,P_y,P_w,P_h\right)=\left({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h\right)$且$\left({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h\right)\approx \left(G_x,G_y,G_w,G_h\right)$

解决方案：先平移，后尺度缩放。

1. 先平移，将$P$的中线点平移到$G$的中心点，假设平移量为$\left(\Delta x,\Delta y\right)$，$\Delta x{=}_w{d}_x\left(P\right),\Delta y=P_h{d}_y\left(P\right)$
2. 后尺度缩放$\left(S_w,S_h\right)$

$$\begin{array}{c}{\hat{G}}_x=P_w{d}_x\left(P\right)+P_x\\ {\hat{G}}_y=P_h{d}_y\left(P\right)+P_y\\ {\hat{G}}_x=P_{w}exp\left(d_w\left(P\right)\right)\\ {\hat{G}}_h=P_{h}exp\left(d_h\left(P\right)\right)\end{array}$$

通过学习这四个函数$d_x\left(P\right),d_y\left(P\right),d_w\left(P\right),d_h\left(P\right)$，我们就可以将proposal bbox $P$转化成为一个预测的ground-truth box $\hat{G}$.

将学习的函数统记为$d_{\ast }\left(P\right),\ast \in \left\{x,y,h,w\right\}$。在RCNN中当$P$和$G$之间的$IoU>0.6$时，可以将$d_{\ast }\left(P\right)$看做一种线性变换，那么我们就可以用线性回归来建模。（在generate target anchor时，认定正样本的一项因素是$IoU>0.7$。$d_{\ast }\left(P\right)$是backbone最后一池化层特征（$poo{l}_5$）的线性函数，表示为$d_{\ast }\left(P\right)=w_{\ast }^T{\varnothing }_5\left(P\right)$，其中$w_{\ast }$是学习到的参数向量，可以通过优化正则最小二乘法目标函数学习得到。
$$w_{\ast }=argmi{n}_{{\hat{w}}_{\ast }}\sum _i^N{\left(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varnothing }_5\left(P^i\right)\right)}^2+\lambda {\Vert {\hat{w}}_x\Vert }^2$$

其中$t_{\ast }$ 是$\left(P,G\right)$的回归目标，定义如下：

$$\begin{array}{c}{t}_x=\left(G_x-P_x\right)/P_w\\ t_y=\left(G_y-P_y\right)/P_h\\ t_w=log\left(G_w/P_w\right)\\ t_h=log\left(G_h/P_h\right)\end{array}$$

proposal

Proposal 层综合回归层和分类的输出，生成Proposal，并通过相应一系列后处理，输出精准的proposal，送去紧接的RoI pooling 层。从proposal层的Caffe Prototxt可以看出，proposal层的输入有三个，回归层输出，分类层输出和图片信息。

layer {
  name: 'proposal'
  type: 'Python'
  bottom: 'rpn_cls_prob_reshape'
  bottom: 'rpn_bbox_pred'
  bottom: 'im_info'
  top: 'rois'
  python_param {
    module: 'rpn.proposal_layer'
    layer: 'ProposalLayer'
    param_str: "'feat_stride': 16"
  }
}

“im_info”，对于任意一张图片大小，在传入Faster RCNN之前会被resize到规定的大小，比如M*N。im_info=[M, N, scale_factor]则保存了此次缩放的所有信息。然后经过backbone之后，4次池化操作下采样，feature_stride=16则保存了该信息，用于计算anchor偏移量。

1. 利用$\left[d_x\left(P\right),d_y\left(P\right),d_w\left(P\right),d_h\left(P\right)\right]$生成predicted boxes在原图中对应的位置$\left(x1,y1,x2,y2\right)$。见下面代码。
2. 在原图中剪裁predicted boxes，移除高和宽小于阈值的predicted boxes
3. 对所有的（proposal，score）按照score从高到低排序，选择前pre_nms_topN (e.g. 6000)
4. 计算NMS，例如设置阈值threshold=0.7，并选择前after_nms_topN (e.g. 300)
5. 返回the top proposal boxes

def bbox_transform_inv(boxes, deltas):
    if boxes.shape[0] == 0:
        return np.zeros((0, deltas.shape[1]), dtype=deltas.dtype)

    boxes = boxes.astype(deltas.dtype, copy=False)

    widths = boxes[:, 2] - boxes[:, 0] + 1.0
    heights = boxes[:, 3] - boxes[:, 1] + 1.0
    ctr_x = boxes[:, 0] + 0.5 * widths
    ctr_y = boxes[:, 1] + 0.5 * heights

    dx = deltas[:, 0::4]
    dy = deltas[:, 1::4]
    dw = deltas[:, 2::4]
    dh = deltas[:, 3::4]

    pred_ctr_x = dx * widths[:, np.newaxis] + ctr_x[:, np.newaxis]
    pred_ctr_y = dy * heights[:, np.newaxis] + ctr_y[:, np.newaxis]
    pred_w = np.exp(dw) * widths[:, np.newaxis]
    pred_h = np.exp(dh) * heights[:, np.newaxis]

    pred_boxes = np.zeros(deltas.shape, dtype=deltas.dtype)
    # x1
    pred_boxes[:, 0::4] = pred_ctr_x - 0.5 * pred_w
    # y1
    pred_boxes[:, 1::4] = pred_ctr_y - 0.5 * pred_h
    # x2
    pred_boxes[:, 2::4] = pred_ctr_x + 0.5 * pred_w
    # y2
    pred_boxes[:, 3::4] = pred_ctr_y + 0.5 * pred_h

    return pred_boxes

下面是截取的参数设置，结合上面描述，食用更佳。

## TRAIN
# IOU >= thresh: positive example
__C.TRAIN.RPN_POSITIVE_OVERLAP = 0.7
# IOU < thresh: negative example
__C.TRAIN.RPN_NEGATIVE_OVERLAP = 0.3
# If an anchor statisfied by positive and negative conditions set to negative
__C.TRAIN.RPN_CLOBBER_POSITIVES = False
# Max number of foreground examples
__C.TRAIN.RPN_FG_FRACTION = 0.5
# Total number of examples
__C.TRAIN.RPN_BATCHSIZE = 256
# NMS threshold used on RPN proposals
__C.TRAIN.RPN_NMS_THRESH = 0.7
# Number of top scoring boxes to keep before apply NMS to RPN proposals
__C.TRAIN.RPN_PRE_NMS_TOP_N = 12000
# Number of top scoring boxes to keep after applying NMS to RPN proposals
__C.TRAIN.RPN_POST_NMS_TOP_N = 2000
# Proposal height and width both need to be greater than RPN_MIN_SIZE (at orig image scale)
__C.TRAIN.RPN_MIN_SIZE = 16

## TEST
## NMS threshold used on RPN proposals
__C.TEST.RPN_NMS_THRESH = 0.7
## Number of top scoring boxes to keep before apply NMS to RPN proposals
__C.TEST.RPN_PRE_NMS_TOP_N = 6000
## Number of top scoring boxes to keep after applying NMS to RPN proposals
__C.TEST.RPN_POST_NMS_TOP_N = 300
# Proposal height and width both need to be greater than RPN_MIN_SIZE (at orig image scale)
__C.TEST.RPN_MIN_SIZE = 16

参考

1. py-faster-rcnn
2. Rich feature hierarchies for accurate object detection and semantic segmentation