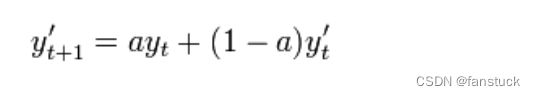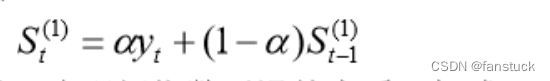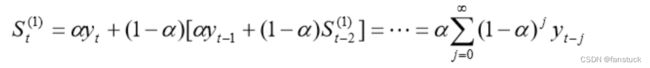一文速学-时间序列分析算法之指数平滑法详解+Python代码实现
目录
前言
一、指数平滑法
1.简介
2.特点
3.基本原理
4.优缺点
优点
缺点
二、一次指数平滑法
1.预测原理及公式
2.加权系数的选择
3.初始值的确定
4.实例运用
点关注，防走丢，如有纰漏之处，请留言指教，非常感谢
参阅
前言
前两篇文章已经将时间序列分析算法的移动平均法系列讲的很详细清晰了：
一文速学-时间序列分析算法之加权移动平均法详解+Python代码实现
一文速学-时间序列分析算法之一次移动平均法和二次移动平均法详解+实例代码
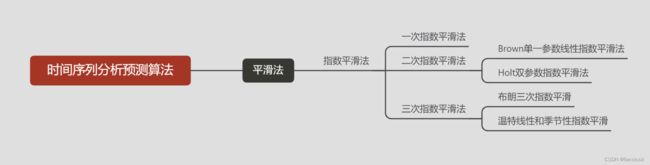
相信大家看完都有一定的计算基础以及理解时序预测算法要做的事情，计算原理无非就是根据时间滑窗来预测计算出下一个时间段数据，就是采取的运算策略和运用场景不同，需要选择相应的算法去支撑。指数平滑法总共有三种形式：
指数平滑法实际上是一种特殊的加权移动平均法，之前我们在code加权移动平均法就发现仅凭自己设定权重是一件比较不可靠的事，如果遇到变化并不平缓明显的数据时并不能很好的计算出结果。倘若权重能够根据实际情况自我训练调整，那么加权移动平均法就更加有作用。下面就我们来了解指数平滑法是如何做到权重变化的吧。
一、指数平滑法
1.简介
指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测，所有预测方法中，指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；而指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。
那么我们以一种通俗易懂的方式来说明：假如我们现在在驾校练车，第一秒的速度为5km/h，第二秒的速度为8km/h，第三秒的速度为10km/h，那么随着时间推进，对于下一个秒数来说，肯定上一秒的数据影响力更大一些。那么我们再来看看接下来的时间段内，数十秒之后，倘若上一时刻的速度的权重为0.9，那么下一时刻经过完了，该权重则需要进行下调。假设随着时间变化权重以指数的方式下降，最近为0.9，那么下一个预测时间段就为
，下下一个预测时间段为
,以此类推...。将权重按照指数级进行衰减，这就是指数平滑法的基本思想。
指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列，三次指数平滑法针对有趋势也有季节性的序列。“Holt-Winters”有时特指三次指数平滑法。
2.特点
第一，指数平滑法进一步加强了观察期近期观察值对预测值的作用，对不同时间的观察值所赋予的权数不等，从而加大了近期观察值的权数，使预测值能够迅速反映实际的变化。
第二，指数平滑法对于观察值所赋予的权数有伸缩性，可以取不同的权值以改变权数的变化速率。如权值取小值，则权数变化较迅速，观察值的新近变化趋势较能迅速反映于指数移动平均值中。因此，运用指数平滑法，可以选择不同的权值来调节时间序列观察值的均匀程度(即趋势变化的平稳程度)。
3.基本原理
也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均 。根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数。
4.优缺点
优点
- 指数平滑法数据需求量小，只需要少数数据即可对未来需求进行预测，对数据存储的需求也非常小，易于进行系统化和自动化。
- 而且计算也相对比较简单，进行预测建模操作也简单，容易理解且运行成本低。
- 自适应指数平滑法克服了平滑系数
值的选择问题，具有自适应性，预测模型能够自动识别数据变化而加以调整。 - Holt双参数指数平滑法和Holt-Winters三参数指数平滑法使用多个平滑系数，能有效的预测和把握时间序列未来的趋势和季节性，从而有效的应对时间序列的变化。
缺点
- 指数平滑法预测一句来源于历史数据，无法识别诸如价格，广告实时变化波动等因果因素带来的需求变化，不能利用解析性变量进行需求塑造。
- 指数平滑法较难找到最优的指数平滑系数，对需求变化的调整存在滞后性，无法一定时间内需求突变进行预测。
- 指数平滑法能很好的预测未来1-3期的需求，但对于更远时期的预测效果不佳。因此指数平滑法只适合做短期预测。
二、一次指数平滑法
1.预测原理及公式
设时间序列为
为加权系数，
，一次指数平滑公式为：
为t+1时刻的预测值，即t时刻的平滑值
,
为t时刻的实际值；
为
时刻的预测值，即为上一时刻的平滑值
.很明显该公式是由移动平均公式改进而来。
上一章我们知道移动平均数的递推公式为：
以
作为
的最佳估计，则有
令,以代替,即得
我们可以试着把该公式展开，会发现：
表明
是全部历史数据的加权平均，加权系数分别为显然有：
由于加权系数符合指数规律，又具有平滑数据的功能，故称为指数平滑。以这种平滑值进行预测，就是一次指数平滑法。预测模型为：
即：
也就是以第t时刻指数平滑值作为t+1时刻预测值。
可以看出，在指数平滑法中，所有先前的观测值都对当前的平滑值产生了影响，但它们所起的作用随着参数 的幂的增大而逐渐减小。那些相对较早的观测值所起的作用相对较小。同时，称 α 为记忆衰减因子可能更合适——因为 α 的值越大，模型对历史数据“遗忘”的就越快。从某种程度来说，指数平滑法就像是拥有无限记忆（平滑窗口足够大）且权值呈指数级递减的移动平均法。
2.加权系数的选择
在进行指数平滑时，加权系数的选择是很重要的。的大小规定了在新预测值中新数据和原预测值所占的比重。值越大，新数据所占的比重就越大，原预测值所占的比重就越小，反之亦然。
从上面可以看出，新预测值是根据预测误差对原预测值进行修正而得到的。的大小则体现了修正的幅度，值越大，修正幅度越大，反之越小。
若选取=0，则
，即下期预测值就等于本期预测值，在预测过程中不考虑任何新信息；若选取=1，则
，即下期预测值就等于本期观测值，完全不相信过去的信息。这两种极端情况很难做出正确的预测。因此，值应根据时间序列的具体性质在0~1之间选择。具体如何选择一般可遵循下列原则：
- 如果时间序列波动不大，比较平稳，则应取小一点，如（0.1~0.5）。以减少修正幅度，使预测模型能包含较长时间序列的信息；
- 如果时间序列具有迅速且明显的变化倾向，则应取大一点，如（0.6~0.8）。使预测模型灵敏度高一些，以便迅速跟上数据的变化。
在实际运用上，类似移动平均法，多几个值进行试算，看哪个预测误差小，就采用哪个。
3.初始值的确定
用一次指数平滑法进行预测，除了选择合适的外，还要确定初始值
。初始值是由预测值估计或指定的。当时间序列的数据较多，比如20个以上，初始值对以后的预测值影响很少，可选用第一期数据为初始值。如果时间序列的数据较少，在20以下时，初始值对以后的预测值影响很大，这时就必须认真研究如何正确确定初始值。一般以最初几期实际值的平均值作为初始值。
4.实例运用
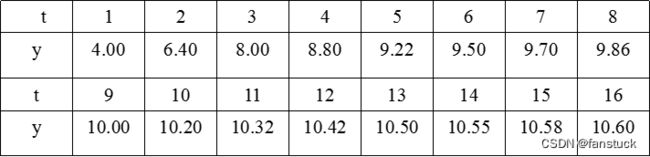
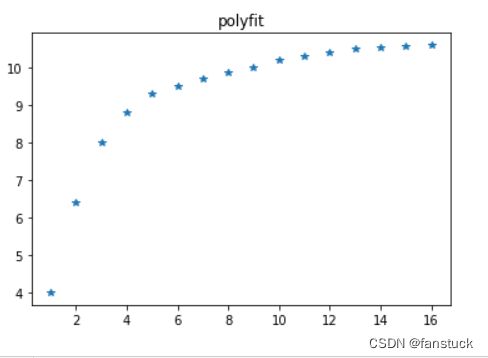
一次指数平滑法相对很简单，我们仍然以某化学反应里，测得生成物浓度y（%）与时间t（min）的数据为例子：
我们以t为15的时刻对应的数值来预测第16时刻的值
#输入预测集合y以及时间窗口数n,a为加权系数
def SES(y,n,a):
y_S=[]
S_0=0
for i in range(n):
S_0=y[i]+S_0
S_0=S_0/n
for i in range(0,y.size):
S_i=a*y[i]+(1-a)*S_0
y_S.append(S_i)
S_0=S_i
return y_S
y1=SES(y,3,0.2)
y2=SES(y,3,0.5)
y3=SES(y,3,0.8)当为0.2时15时刻为10.02，当为为0.5时为10.52，当为0.8时为10.57
那么我们以 为0.8时为例：
由上述例题可得结论：
- 指数平滑法对实际序列具有平滑作用，权系数（平滑系数）a 越小，平滑作用越强，但对实际数据的变动反应较迟缓。
- 在实际序列的线性变动部分，指数平滑值序列出现一定的滞后偏差的程度随着权系数（平滑系数）a 的增大而减少，但当时间序列的变动出现直线趋势时，用一次指数平滑法来进行预测仍将存在着明显的滞后偏差。因此，也需要进行修正。修正的方法也是在一次指数平滑的基础上再进行二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型，故称为二次指数平滑法。
点关注，防走丢，如有纰漏之处，请留言指教，非常感谢
以上就是本期全部内容。我是fanstuck ，有问题大家随时留言讨论 ，我们下期见。
参阅
指数平滑法（Exponential Smoothing，ES）
指数平滑法
指数平滑法的优缺点和最佳应用范围
时间序列模型 （三）：指数平滑法