【数模系列】02_三大相关系数+Python代码
文章目录
- 一、皮尔逊相关系数
-
- 1、公式推导
- 2、使用条件
- 3、Python绘图
- 二、斯皮尔曼秩相关系数
-
- 1、如何选择皮尔逊和斯皮尔曼
- 三、肯德尔秩相关系数
一、皮尔逊相关系数
在统计学中,皮尔逊相关系数,是用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间,其绝对值越大说明该两个变量越相关。
注意:该系数只能评价两个线性变量之间的相关性。
1、公式推导
①首先由Pearson相关系数的定义可知,
ρ x , y = c o v ( X , Y ) σ X σ Y ρ_{x,y}=\frac{cov(X,Y)}{σ_X σ_Y} ρx,y=σXσYcov(X,Y)
②这里,分子cov表示协方差,分母表示标准差(以两个变量为例):
c o v ( X , Y ) = ∑ i = 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) n − 1 cov(X,Y)=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{n-1} cov(X,Y)=n−1∑i=1n(Xi−X)(Yi−Y)
③皮尔逊相关系数:
ρ = ∑ i = 1 N ( x i − x ‾ ) ( y i − y ‾ ) [ ∑ i = 1 N ( x i − x ‾ ) 2 ∑ i = 1 N ( y i − y ‾ ) 2 ] 1 2 ρ=\frac{\sum_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{[\sum_{i=1}^N(x_i-\overline{x})^2\sum_{i=1}^N(y_i-\overline{y})^2]^{\frac{1}{2}}} ρ=[∑i=1N(xi−x)2∑i=1N(yi−y)2]21∑i=1N(xi−x)(yi−y)
2、使用条件
Pearson相关系数可用于衡量变量之间的线性相关程度,但有一定的使用条件:
1、在计算皮尔逊相关系必须用spss画出各个变量之间的散点图(相关性可视化)。当然也可以用其他软件,如excel,matlab。若两个变量的散点图呈线性的关系,则可以用皮尔逊相关系数。反之,则不能用。
2、然后再判断总体数据是否满足正态分布。例如:如果你要比较5个变量两两的相关性,这时就要进行判断,方法有很多种,后面会提到。
注意:若以上条件有一不满足,则不能用皮尔逊相关系数。总之,要用皮尔逊相关系数必须满足连续数据,正态分布,线性关系。
3、Python绘图
data.corr(method="pearson")#皮尔逊系数
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
myfont=FontProperties(fname=r'C:\Windows\Fonts\simhei.ttf',size=40)
sns.set(font=myfont.get_name(), color_codes=True)
#corr = df.corr(method='pearson') # 使用皮尔逊系数计算列与列的相关性
#corr = df.corr(method='kendall') # 肯德尔秩相关系数
#corr = df.corr(method='spearman') # 斯皮尔曼秩相关系数
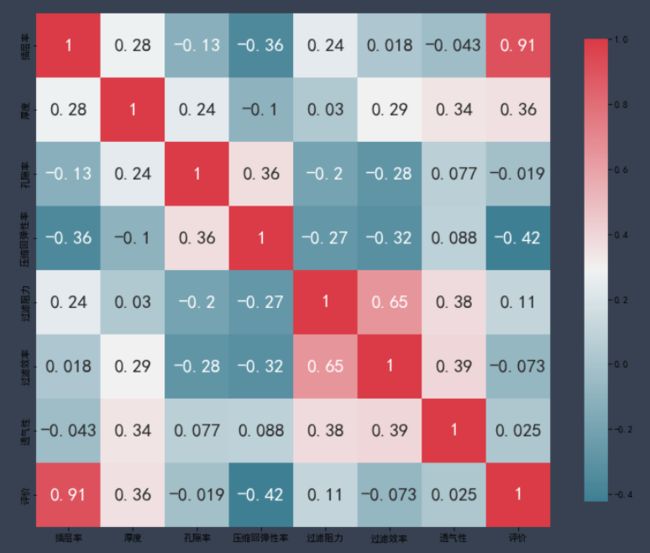
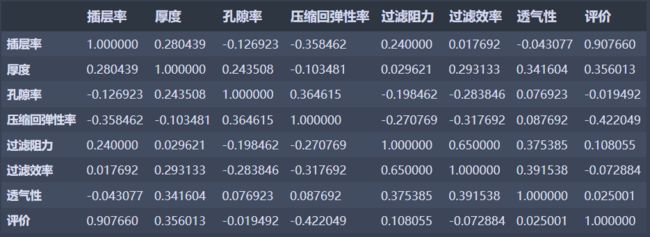
data_corr = data.corr(method='pearson') # 使用皮尔逊系数计算列与列的相关性
plt.figure(figsize=(20,15))#figsize可以规定热力图大小
fig=sns.heatmap(data_corr,annot=True,fmt='.2g',annot_kws={'fontsize': 20})#annot为热力图上显示数据;fmt='.2g'为数据保留两位有效数字
fig
fig.get_figure().savefig('dingding_corr.png')#保留图片
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns # 可视化w
inputdata = pd.read_csv('chazhi55.csv')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
df = inputdata.copy()
_, ax = plt.subplots(figsize=(13, 10)) # 分辨率1200×1000
#corr = df.corr(method='pearson') # 使用皮尔逊系数计算列与列的相关性
#corr = df.corr(method='kendall') # 肯德尔秩相关系数
corr = df.corr(method='spearman') # 斯皮尔曼秩相关系数
# 上面三行代表了不同的计算方法,需要哪个就把其他的备注就好
cmap = sns.diverging_palette(220, 10, as_cmap=True) # 在两种HUSL颜色之间制作不同的调色板。图的正负色彩范围为220、10,结果为真则返回matplotlib的colormap对象
_ = sns.heatmap(
corr, # 使用Pandas DataFrame数据,索引/列信息用于标记列和行
cmap=cmap, # 数据值到颜色空间的映射
square=True, # 每个单元格都是正方形
cbar_kws={'shrink': .9}, # `fig.colorbar`的关键字参数
ax=ax, # 绘制图的轴
annot=True, # 在单元格中标注数据值
annot_kws={'fontsize': 20}) # 热图,将矩形数据绘制为颜色编码矩阵
plt.show()
plt.get_figure().savefig('斯皮尔曼秩相关系数热力图.png')#保留图片
二、斯皮尔曼秩相关系数
斯皮尔曼的计算公式为:
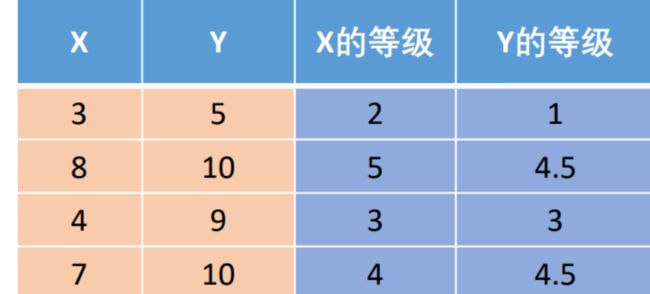
p = 1 − 6 ∑ d i 2 n 3 − n , 其中 d i 表示顺序的差值, n 表示数据个数。 p=1-\frac{6\sum d^2_i}{n^3-n} ,其中di表示顺序的差值,n表示数据个数。 p=1−n3−n6∑di2,其中di表示顺序的差值,n表示数据个数。
斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数。等级按照从小到大排序。
满足皮尔逊相关系数的使用条件和检验条件则使用皮尔逊相关系数。
只要其中一个条件不满足则使用斯皮尔曼等级相关系数。另外两个定序数据之间的相关系数求解也用斯皮尔曼。斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广。
1、如何选择皮尔逊和斯皮尔曼
皮尔逊相关系数和斯皮尔曼相关系数:
-
如果数据是连续的、正态分布的,并且是线性的,优先使用皮尔逊相关系数。当然,也可以使用斯皮尔曼,但效率没有皮尔逊高(因为要进行排序)。

-
如果前面几个条件有一个不满足,则使用斯皮尔曼相关系数;皮尔逊相关系数适用于线性关系,而斯皮尔曼相关系数适用于单调关系,线性与单调的一个区别是,线性关系的斜率是固定的。

-
如果数据看上去,既有点像线性关系,又有点像单调关系,那么使用斯皮尔曼相关系数;皮尔逊相关系数使用元数据进行计算的,而斯皮尔曼相关系数是基于秩计算的。
data.corr(method="spearman")#斯皮尔曼秩相关系数
三、肯德尔秩相关系数
肯德尔相关性系数,又称肯德尔秩相关系数,它也是一种秩相关系数,不过它所计算的对象是分类变量。
分类变量可以理解成有类别的变量,可以分为:
- 无序的,比如性别(男、女)、血型(A、B、O、AB);
- 有序的,比如肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)。
通常需要求相关性系数的都是有序分类变量。举个例子。比如评委对选手的评分(优、中、差等),我们想看两个(或者多个)评委对几位选手的评价标准是否一致;或者医院的尿糖化验报告,想检验各个医院对尿糖的化验结果是否一致,这时候就可以使用肯德尔相关性系数进行衡量。
data.corr(method="kendall")#肯德尔秩相关系数