卷积神经网络——24位彩色图像的卷积的详细介绍
卷积用于图像处理:
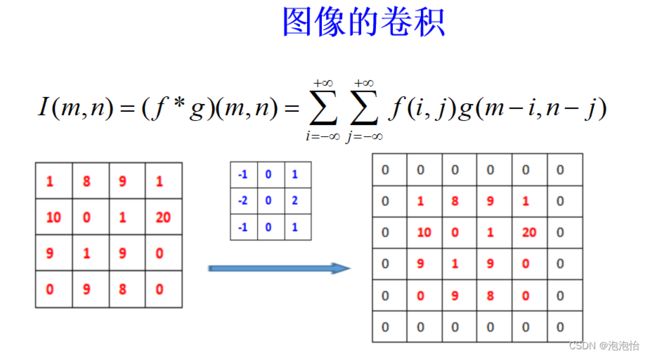
卷积在函数方面的表现是一种连续的,可以用积分来表示,其实在初识积分的时候,我们就知道积分是通过离散数据求和得来的,这也决定了图像处理也可以运用到卷积的原理。在电脑中,图像其实是一个m*n的矩阵(这里不讨论颜色通道),那么针对于像素点,我们可以使用卷积的原理,使用另一个矩阵,将图像的低阶特征去除掉,保留和突出图像的高阶特征,再根据后续操作,对图像进行分类或者识别。
在连续函数的卷积中,使用的是可移动的与f(x)进行积分,在离散的图像矩阵中,将采取一种“卷积核”的特殊矩阵,它的作用就是代替,在平移的过程中与图像矩阵相乘累加,从而达到卷积中积分的效果。
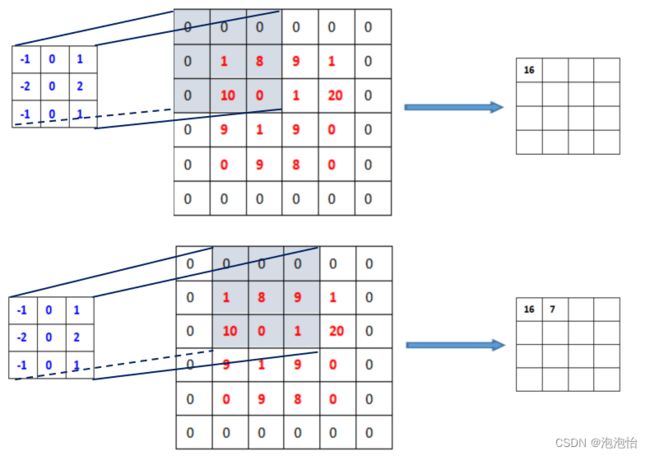
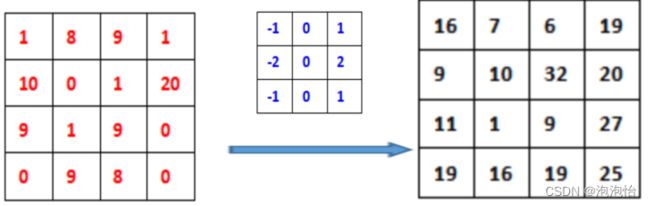
卷积在图像处理中经常被用于平滑、模糊、锐化、去噪、边缘取等工作中。图像处理中的卷积操作,其实就是利用卷积核(模板)在目标图像上滑动,将图像上的像素点依次对应到卷积核的中间像素处,每个像素点对齐后将图像上的像素灰度值与卷积核对应位置上的数值相乘,然后将相乘后的所有值相加,相加的结果作为当前像素的灰度值,并最终滑动完所有图像像素点的过程。
一、24位彩色图像的卷积
1.导包
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt2.符号说明:
输入参数:
im : 单通道图像 mfilter:滤波器 fm:滤波器行数 fn:滤波器列数 hfm:滤波器行数半径 hfn:滤波器列数半径 输出参数 :convIm:单通道卷积结果
3.定义卷积运算的函数:
def convolution( im, mfilter, fm, fn, hfm, hfn ):
mI, nI = im.shape
imp = np.pad( im, (hfm, hfn ), 'constant' )
padmI, padnI = imp.shape
convHeight = padmI - fm + 1
convWidth = padnI - fn + 1
convIm = np.zeros( (mI, nI), dtype=np.float )
for i in range( convHeight ):
for j in range( convWidth ):
locIm = imp[ i:i+fm, j:j+fn ]
convIm[i][j] = np.sum( locIm * mfilter )
convIm = convIm.clip( 0, 255 )
convIm = np.rint(convIm).astype('uint8')
return convIm4.对rgb三通道图片的每一个通道调用卷积运算函数进行卷积操作,输出卷积之后的图片。
def ImageConvolution( image, mfilter ):
mI, nI, cI = np.shape( image )
print( 'Image size:', mI, nI, cI )
[fm, fn] = np.shape( mfilter )
print( 'fileter size:', fm, fn )
hfm = int( fm / 2 )
hfn = int( fn / 2 )
#根据滤波器长度奇偶性的不同调整扩充图像的范围
if fn % 2 == 0:
hfn -= 1
imR = image[ :, :, 0 ]
imG = image[ :, :, 1 ]
imB = image[ :, :, 2 ]
#依次截取与滤波器大小相同的图像块进行内积运算
convImageR = convolution( imR, mfilter, fm, fn, hfm, hfn )
convImageG = convolution( imG, mfilter, fm, fn, hfm, hfn )
convImageB = convolution( imB, mfilter, fm, fn, hfm, hfn )
convImage = np.stack( ( convImageR, convImageG, convImageB ), 2 )
return convImage
5.主函数就是输入需要处理的图片,然后调用刚刚第二个函数对图片进行卷积操作,最后可视化卷积之后的图片
def main():
img = np.array( Image.open("C:/Users/bwy/Desktop/暑假/ImageConvolution_py/1.jpg", 'r') )
plt.figure( 'Image' )
plt.imshow( img )
#plt.axis( 'off' )
#根据滤波器对图像进行卷积
filter1 = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1] ]
imageConv = ImageConvolution( img, filter1 )
plt.figure( 'filter1' )
plt.imshow( imageConv )
plt.axis( 'off' )
filter2 = np.ones( (2, 2) )
filter2 /= filter2.sum()
imageConv = ImageConvolution( img, filter2 )
plt.figure( 'filter2x2' )
plt.imshow( imageConv )
plt.axis( 'off' )
filter2 = np.ones( (3, 3) )
filter2 /= filter2.sum()
imageConv = ImageConvolution( img, filter2 )
plt.figure( 'filter3x3' )
plt.imshow( imageConv )
plt.axis( 'off' )
filter2 = np.ones( (4, 4) )
filter2 /= filter2.sum()
imageConv = ImageConvolution( img, filter2 )
plt.figure( 'filter4x4' )
plt.imshow( imageConv )
plt.axis( 'off' )
if __name__ == '__main__':
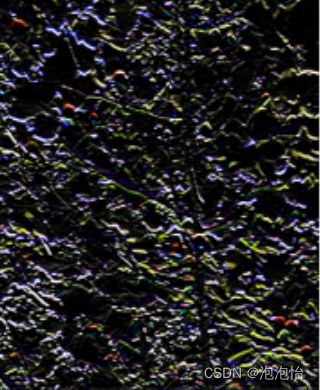
main()结果:左图(原图像):
完整全部代码如下:
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
#卷积
#输入参数:
# im : 单通道图像
# mfilter:滤波器
# fm:滤波器行数
# fn:滤波器列数
# hfm:滤波器行数半径
# hfn:滤波器列数半径
#输出参数:
# convIm:单通道卷积结果
def convolution( im, mfilter, fm, fn, hfm, hfn ):
mI, nI = im.shape
imp = np.pad( im, (hfm, hfn ), 'constant' )
padmI, padnI = imp.shape
convHeight = padmI - fm + 1
convWidth = padnI - fn + 1
convIm = np.zeros( (mI, nI), dtype=np.float )
for i in range( convHeight ):
for j in range( convWidth ):
locIm = imp[ i:i+fm, j:j+fn ]
convIm[i][j] = np.sum( locIm * mfilter )
convIm = convIm.clip( 0, 255 )
convIm = np.rint(convIm).astype('uint8')
return convIm
#图像的卷积运算
#输入参数
# image:原图像
# mfilter:滤波器
#输出参数
# convImage:卷积后的图像
def ImageConvolution( image, mfilter ):
mI, nI, cI = np.shape( image )
print( 'Image size:', mI, nI, cI )
[fm, fn] = np.shape( mfilter )
print( 'fileter size:', fm, fn )
hfm = int( fm / 2 )
hfn = int( fn / 2 )
#根据滤波器长度奇偶性的不同调整扩充图像的范围
if fn % 2 == 0:
hfn -= 1
imR = image[ :, :, 0 ]
imG = image[ :, :, 1 ]
imB = image[ :, :, 2 ]
#依次截取与滤波器大小相同的图像块进行内积运算
convImageR = convolution( imR, mfilter, fm, fn, hfm, hfn )
convImageG = convolution( imG, mfilter, fm, fn, hfm, hfn )
convImageB = convolution( imB, mfilter, fm, fn, hfm, hfn )
convImage = np.stack( ( convImageR, convImageG, convImageB ), 2 )
return convImage
def main():
img = np.array( Image.open("C:/Users/bwy/Desktop/暑假/ImageConvolution_py/1.jpg", 'r') )
plt.figure( 'Image' )
plt.imshow( img )
#plt.axis( 'off' )
#根据滤波器对图像进行卷积
filter1 = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1] ]
imageConv = ImageConvolution( img, filter1 )
plt.figure( 'filter1' )
plt.imshow( imageConv )
plt.axis( 'off' )
filter2 = np.ones( (2, 2) )
filter2 /= filter2.sum()
imageConv = ImageConvolution( img, filter2 )
plt.figure( 'filter2x2' )
plt.imshow( imageConv )
plt.axis( 'off' )
filter2 = np.ones( (3, 3) )
filter2 /= filter2.sum()
imageConv = ImageConvolution( img, filter2 )
plt.figure( 'filter3x3' )
plt.imshow( imageConv )
plt.axis( 'off' )
filter2 = np.ones( (4, 4) )
filter2 /= filter2.sum()
imageConv = ImageConvolution( img, filter2 )
plt.figure( 'filter4x4' )
plt.imshow( imageConv )
plt.axis( 'off' )
if __name__ == '__main__':
main()博主收到的一树“杏运”,每位读到这篇文章的人也都会超级幸运,运气爆好!!!