opencv图像处理进阶——灰度直方图

1、灰度直方图概念

灰度直方图反映一幅图像中各灰度级像素出现的频率与灰度级的关系，其中，灰度级为横坐标，频率为纵坐标。

灰度级：图像中不同灰度的最大数量，灰度级越大，图像亮度范围越大。

2、灰度直方图的性质

（1)   只反映图像灰度情况，不反映像素位置；

（2）一幅图像对应唯一的灰度直方图，但同一灰度直方图可能对应多幅图像；

（3）一幅图像划分多个区域，这些区域的直方图之和为原图像直方图。

3、灰度直方图的作用

（1）在使用轮廓线确定物体边界时，通过直方图更好地选择边界阈值，进行阈值化处理；

（2）对物体与背景有较强的对比的景物分割特别有用；

（3）简单物体的面积和综合光密度IOD可以通过直方图求得。

4、绘制灰度直方图的两种方法

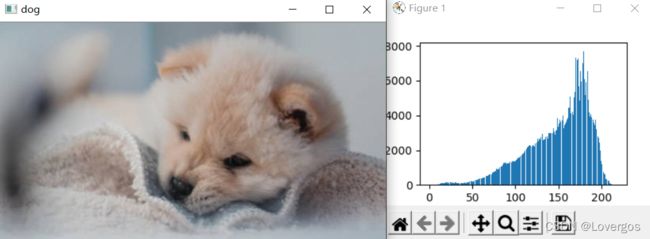
方法1、matplotlib：hist(数据源,像素级)

注意：数据源必须是一维数组，因此需要使用ravel()函数将图像降为一维数组。

# 方法1：matplotlib——hist()
img = cv2.imread(r'F:\lovergos\OpenCV\Image\dog.jpg')
cv2.imshow('dog',img)
plt.hist(img.ravel(),256)
plt.show()
cv2.waitKey(0)

 方法2：cv2.calcHist(images, channels, mask, histSize, ranges, accumulate)

常用参数说明：images表示输入原始图像；channels表示通道，对于灰度图为[0]；彩色图B、G、R分别用[0]、[1]、[2]表示；mask表示掩码图像，没有则使用None；ranges表示像素值范围。

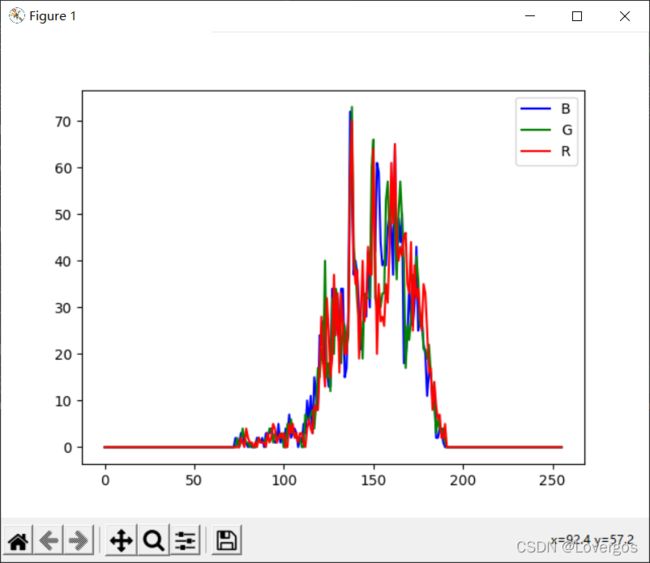
# 方法2 opencv——calHist()
img = cv2.imread(r'F:\lovergos\OpenCV\Image\ch.png')
img_b = cv2.calcHist(img,[0],None,[256],[0,255])  # B分量灰度图的直方图
img_g = cv2.calcHist(img,[1],None,[256],[0,255])  # G分量灰度图的直方图
img_r = cv2.calcHist(img,[2],None,[256],[0,255])  # R分量灰度图的直方图

plt.plot(img_b,color='b',label='B')
plt.plot(img_g,color='g',label='G')
plt.plot(img_r,color='r',label='R')
plt.legend()
plt.show()

5、直方图均衡化

基本原理：对在图像中像素个数多的灰度值进行展宽，，而对像素个数少的灰度值进行归并，从而增大对比度，使图像更加清晰。

直方图均衡化的实现步骤：

  本文以一个简单例子来实现直方图均衡化。假设以下图像的灰度级范围是[0,5]

 [1    5    3]
 [2    4    5]
 [3    1    0]
 

（1）计算原始图像的灰度直方图：[1 , 2 , 2 , 1 , 1 , 2]

（2）计算原图总像素个数 N = 3 * 3 = 9

（3）计算原图灰度分布频率：[1/9 , 2/9 , 2/9 , 1/9 , 1/9 , 2/9]

（4）计算原图累计分布频率：[1/9 , 3/9 , 5/9 , 6/9 , 7/9 , 9/9]

（5）将累计分布中的元素乘以(L-1)(L-1为灰度级最大值，本例中L-1=5），再四舍五入，以使得均衡化后的图像的灰度级与原始图像一致。

s[0] = 1/9 * 5 = 0; s[1] = 3/9 * 5 = 2; s[2] = 5/9 * 5 = 3;

s[3] = 6/9 * 5 = 3; s[4] = 7/9 * 5 = 4; s[5] = 9/9 * 5 = 5;

s = [0 , 2 , 3 , 3 , 4 , 5]

注意：原图中的值作为s的下标，对应的值即为均衡化后的结果：

 [2    5    3]
 [3    4    5]
 [3    2    0]

为了更好的演示算法原理，本文首先通过自行编码实现灰度图像的直方图均衡化，然后再对比opencv实现均衡化方法来验证。

（1）首先读取一张灰度图，并提取其高度和宽度

import cv2
import numpy as np
import matplotlib.pyplot as plt

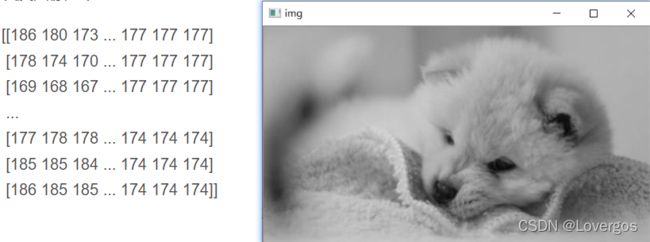
img = cv2.imread(r'F:\lovergos\OpenCV\Image\dog.jpg',cv2.IMREAD_GRAYSCALE)  # 读取一张灰度图
height,width = img.shape  

灰度图像如下：

（2）统计每个灰度像素值的累计数目，构建初始灰度直方图

num_pixel = np.zeros(256)  # 创建长度为256的列表，用来保存每个像素值的数目，初始化为0

# 统计列表中某个值出现的次数
for i in range(height):
    for j in range(width):
        k = img[i][j]  # 得到当前像素值
        num_pixel[k] = num_pixel[k]+1  # 当前像素值的个数增加1(k的大小对应num_pixel的下标）

# 显示灰度直方图
# plt.bar(np.arange(0,256),num_pixel)
# plt.show()

（3）计算原图灰度分布频率

prob_pixel = np.zeros(256)
for i in range(0,256):
    prob_pixel[i] = num_pixel[i]/(height*width)  # 出现次数/总数

（4）计算原图累积分布频率：调用np.cumsum()

cum_pixel = np.cumsum(prob_pixel)

（5）将累计分布中的元素乘以(L-1)(此处为255），再四舍五入，以使得均衡化后的图像的灰度级与原始图像一致。

for i in range(len(cum_pixel)):
    cum_pixel[i] = int(cum_pixel[i]*255+0.5)  # python中直接取整不会四舍五入，因此先+0.5再取整表示四舍五入

（6）根据cum_pixel得到形式和原图相同的输出

out_img = img  # 保持和原图格式相同
for m in range(0,height):
    for n in range(0,width):
        k = img[m][n]
        out_img[m][n] = cum_pixel[img[m][n]]  # out_img中新的值，保存在cum_pixel中，由映射关系知，img[m][n]为对应下标

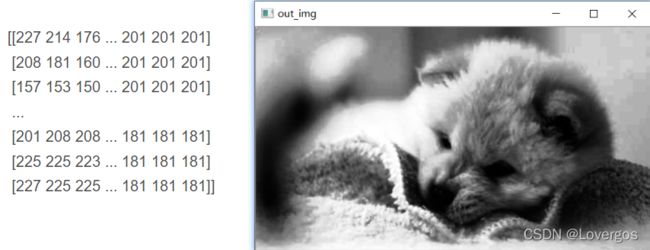
通过这种方式均衡化得到的新图为：

（7）验证：使用opencv中的函数 cv2.equalizeHist(image)

equ = cv2.equalizeHist(img)
print(equ)
cv2.imshow('out_img',equ)
cv2.waitKey(0)

通过观察，两种方法得到的结果是一致的。但不得不说opencv的方法还是简单太多。

参考文献

[1] 图像的灰度直方图_逸凌Time-CSDN博客_灰度直方图

[2] 数字图像处理(15): 灰度直方图(matplotlib 和OpenCV 绘制直方图)_TechArtisan6的博客-CSDN博客[3]【图像处理算法】直方图均衡化_GQ-CSDN博客_直方图均衡化