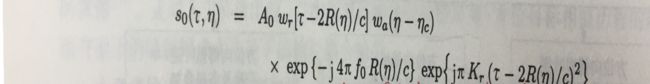SAR—距离向脉冲压缩的一些理解
SAR—距离向脉冲压缩的一些理解
——by snowshow
目录
SAR—距离向脉冲压缩的一些理解
1、如何定义SAR图像空间中目标的距离
2、距离徙动概念
3、脉冲压缩
4、目标在方位向的有效持续照射时间问题
5、探讨同一距离单元不同方位位置的两点距离压缩后的图像
6、距离徙动校正
7、附代码
8、其他一些距离压缩的结果
9、写在最后……
1、如何定义SAR图像空间中目标的距离
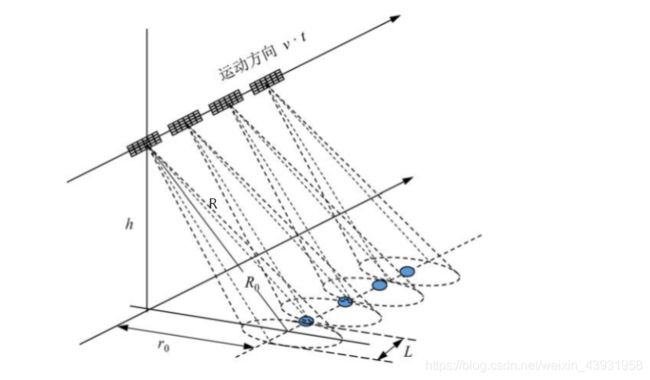
首先先了解“距离”这个概念，距离一般指斜距或者地距，前者是指沿雷达视线方向测量，而后者是沿地面测量。下图中的R0和r0是零多普勒位置（注1）校正后的斜距和地距。
由于所有SAR处理中都使用斜距的定义，如果不加特殊说明，那么一般情况下距离默认为斜距。
我们将距离在信号空间和图像空间中分别来定义。
在信号空间中，距离测量的是雷达天线与地面目标的间隔，假设一波束覆盖区域中的一个目标A,该目标在处于雷达的视线范围内的过程中，随着雷达位置的变化，雷达同目标A的距离也即瞬时斜距也会发生变化。目标A的距离变化如下图所示。雷达传感器到目标点的距离R（η）由双曲线方程给出：
R(η)^2=R0^2+（Vr*η）^2 （1）
其中R0是雷达距离目标最近时的斜距，即最短距离。η是相对于最近点位置的方位之间，我的理解也就是相对于零多普勒时刻的方位时间，比如照射目标被照射到波束时假如雷达还未到达最近点位置，那么此时该η为传感器从该位置到达最近点位置的时间。否则为雷达从最近点位置到达雷达目标所在位置的时间。
经过SAR处理，得到目标在图像空间的聚焦位置，目标在图像空间中被聚焦于与其零多普勒时刻相对应的位置，目标的距离即为雷达传感器同目标最接近的时刻雷达传感器同目标的距离，也就等同于雷达传感器同目标的最近距离（零多普勒位置校准之后的斜距）。由于零多普勒时刻与天线斜视角无关，所以最终图像中目标的位置并不依赖于斜视角。
2、距离徙动概念
如式（1）所示，瞬时斜距R(η)随方位时间η而改变，该式表明目标轨迹（以距离为量纲）是方位时间的函数。在SAR成像中，在一个合成孔径时间内，来自某一点目标的回波信号在不同的时刻处在不同 距离单元的现象叫做距离徙动。
3、脉冲压缩
首先对雷达系统接受到的原始数据解调至基带，以便将距离频率中心置零。解调后的点目标信号模型为如下，
可以通过匹配滤波器来实现距离向的脉冲压缩。距离压缩输出为
pr（t）为 窗函数Wt（ft）的傅里叶逆变换，对于矩形窗，pr（t）为sinc函数。我们可以认为脉压峰值对应的时刻就是回波时延，可以根据此来计算出目标的距离，但是雷达平台在运行过程中，与目标的距离是变化的，这就导致在对于同一目标，雷达不同慢时间时刻上，距离脉冲压缩后的峰值不在同一时刻。即距离压缩后得到的是含有距离徙动的瞬时斜距。
（注：图引用自博客链接https://blog.csdn.net/a1367666195/article/details/106614692）
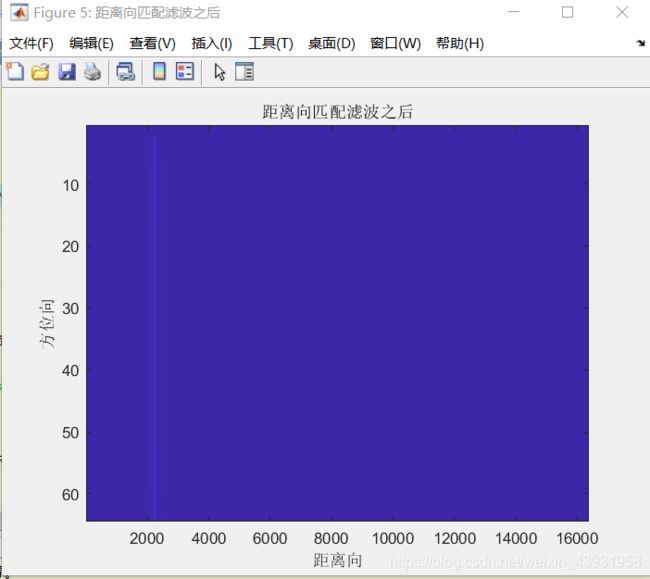
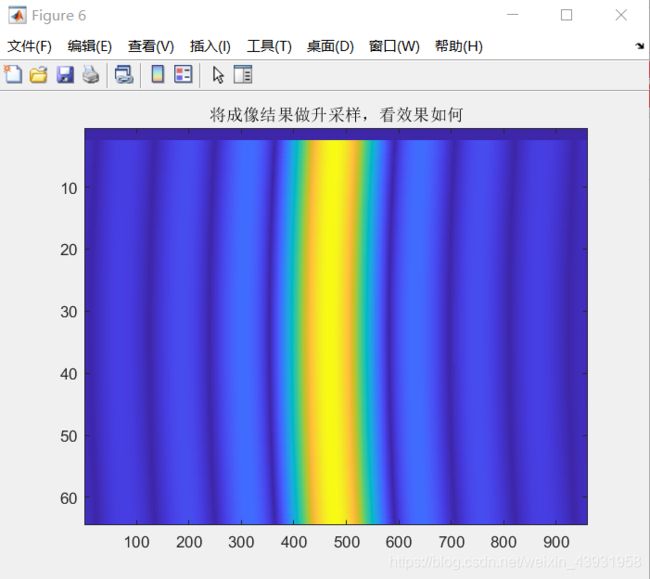
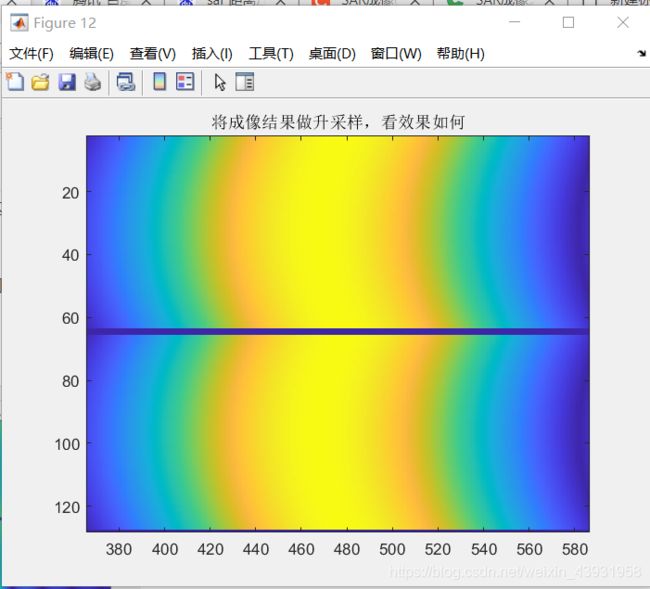
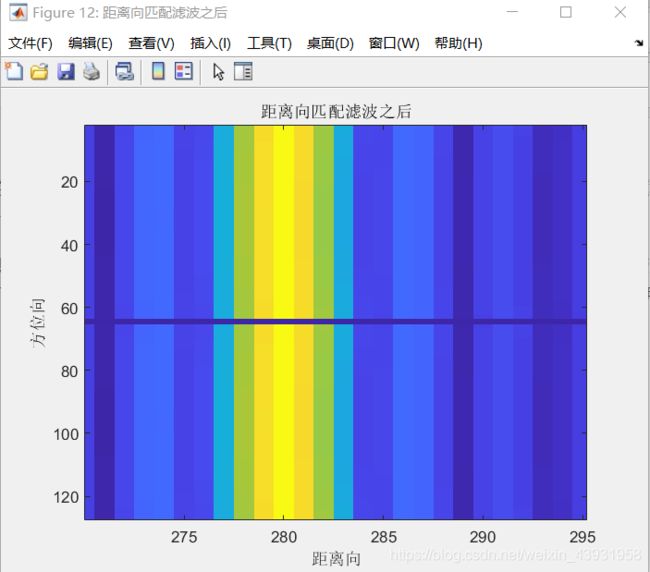
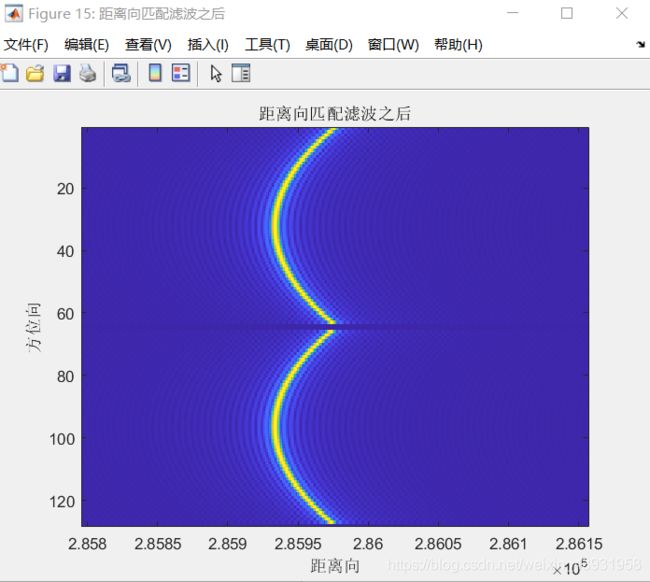
对某一点目标回波脉冲压缩后如下图（左），可能由于距离采样数较低，无法直观看出距离弯曲，对数据进行升采样，得到右图
效果仍不明显，对上（右）图局部放大
4、目标在方位向的有效持续照射时间问题
代码
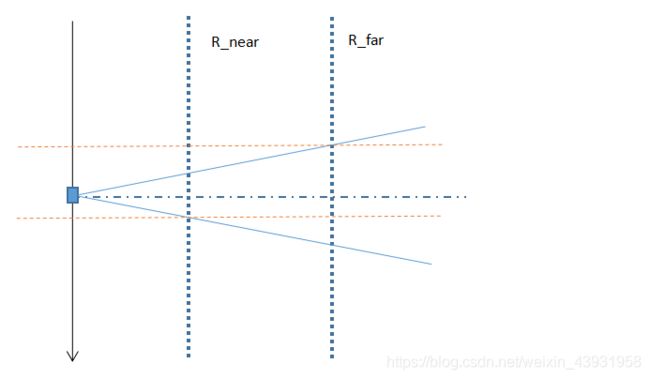
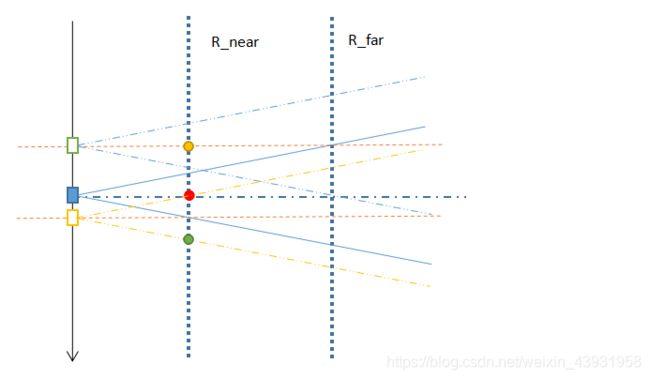
由下图可知，在该方位采样时间内，任一目标并不一定可以得到全孔径的照射时间。
对于目标（R_near,- La_far/2)的回波幅度、相位、匹配滤波结果分别为
对于目标（R_near,La_near/2)的回波幅度、相位、匹配滤波结果分别为
5、探讨同一距离单元不同方位位置的两点距离压缩后的图像
我们选定的两点为下图中的橘色点（R_near,- La_far/2）和绿色点（R_near,La_near/2)
对这两点目标模拟回波信号，并进行匹配滤波得到距离向脉冲压缩的结果，故回波幅度、相位分别为，
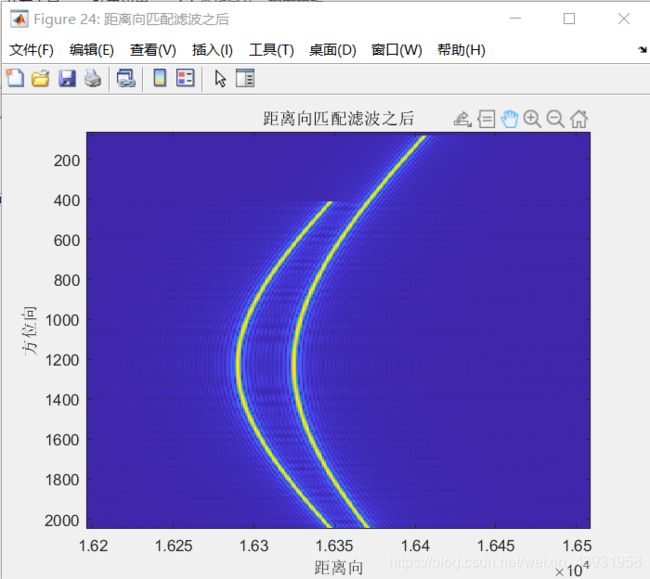
匹配滤波结果、对匹配滤波目标所在区域进行升采样结果、对升采样结果的放大分别为，
由上图也可以看出来，距离压缩之后的位置是符合目标位置同雷达距离（瞬时斜距）的变化的，也可以明显的看出存在距离徙动。在方位范围为[ - La_far/2/Va, La_near/2/Va]，橘色点的距离徙动规律是“距离不断增大”，绿色点则为“距离不断减小”，同图像中显示的规律是相同的。
那为了观察点目标在整个孔径范围的一个距离徙动规律，
我们将方位范围扩展为[- La_far/2/Va - La_near/2/Va, La_near/2/Va+La_near/2/Va],即两边各加一个1/2近距离合成孔径对应时长。则其距离徙动效果为
6、距离徙动校正
待写……
7、附代码
（1）主程序 BP_original.m
%% 多点目标 单站SAR
% 2014/03/17
clc;
clear all;
%close all;
%% parameters
c = 3e8;
j = sqrt(-1);
pi = 3.1416;
fc = 20e9;
lamda = c/fc;
D = 4;
Va = 15000;
a=3;
Kr = 200e12;
Tr = 2.5e-6;
sq_ang = 0/180*pi; %斜视角
Br = Kr*Tr;
Frfactor = 1.2;
Fr = Br*Frfactor; %距离向采样率
Ba = 0.886*2*Va*cos(sq_ang)/D;
Fafactor = 1.2;
Fa = Ba*Fafactor; %方位向采样率
R_near = 2e4;%最近的目标的距离（me）
R_far = R_near + 1000;%最远的目标的距离（me）
La_near = 0.886*R_near*lamda/cos(sq_ang)^2/D; % 近距合成孔径长度
La_far = 0.886*R_far *lamda/cos(sq_ang)^2/D;
Tc_near = -R_near*tan(sq_ang)/Va; % 波束中心时间
Tc_far = -R_far *tan(sq_ang)/Va;
fdc = 2*Va*sin(sq_ang)/lamda; % 多普勒中心频率
Y_min = Va*Tc_far;
Y_max = Y_min+100;
Rmin = sqrt(R_near^2+(Tc_near*Va+La_near/2)^2);
Rmax = sqrt(R_far^2 +(Tc_far*Va -La_far/2)^2);
disp('parameters:');
disp('minimal slant range');disp(Rmin);
disp('maximal slant range');disp(Rmax);
disp('range resolution:');disp(0.886*(c/2/Br));
disp('azimuth resolution:');disp(0.886*(Va/Ba));
disp('doppler centroid frequency');disp(fdc);
%% echo model
Nr = (2*Rmax/c - 2*Rmin/c + Tr)*Fr;
Nr = 2^nextpow2(Nr);
tr = linspace(-Tr/2 + 2*Rmin/c,Tr/2 + 2*Rmax/c,Nr); % 快时间t采样点，最早收到回波~最晚收到回波
Fr = (Nr - 1)/(Tr/2 + 2*Rmax/c - (-Tr/2 + 2*Rmin/c));
% Na = ((Tc_near + La_near/2/Va)-(Tc_far - La_far/2/Va))*Fa;
% Na = 2^nextpow2(Na);
% ta = linspace(Tc_far - La_far/2/Va,Tc_near + La_near/2/Va,Na);% 慢时间采样点
Na = ((Tc_near + 2*La_near/2/Va)-(Tc_far - La_far/2/Va-La_near/2/Va))*Fa;
Na = 2^nextpow2(Na);
ta = linspace(Tc_far - La_far/2/Va-La_near/2/Va,Tc_near + La_near/2/Va+La_near/2/Va,Na);% 慢时间采样点 （增加方位采样时长，尝试）
Fa = (Na -1)/(Tc_near + La_near/2/Va -(Tc_far - La_far/2/Va));
Rpt = [R_near R_near R_near ]; % 点目标距离坐标
Ypt = [-35 33 100 ]; % 点目标方位坐标
La = 0.886*Rpt*lamda/(cos(sq_ang)^2)/D; % .3点目标合成孔径长度
Tc = -Rpt*tan(sq_ang)/Va;
Npt = length(Rpt);
Y_high = max(Ypt) + 50;
Y_low = min(Ypt) - 50;
R_left = R_near - 50;
R_right = R_far + 50;
disp('number of point targets:');disp(Npt);
disp('range sample number:');disp(Nr);
disp('azimuth sample number:');disp(Na);
disp('range sample rate:');disp(Fr);
disp('azimuth sample rate:');disp(Fa);
sig = zeros(Na,Nr);
for k = 1:Npt
%delay = 2/c*sqrt(Rpt(k)^2+(Ypt(k)-1/2*a*ta^2).^2);
delay = 2/c*sqrt(Rpt(k)^2+(Ypt(k)-ta*Va).^2);
Dr = ones(Na,1)*tr - delay'*ones(1,Nr); % t-tao
sig = sig + exp(j*pi*Kr*Dr.^2 - j*2*pi*fc*delay'*ones(1,Nr))... %无须更改\
.*(abs((ta - Ypt(k)/Va - Tc(k))'*ones(1,Nr)) <= La(k)/2/Va)...%仅把波束范围内的信号进行一个保留
.*(abs(Dr) <= Tr/2); %经实验证明，这句话是有用的，去掉此句话会出现重影;这句代码仅仅是表示了脉冲chirp函数的脉冲范围为Tr，[-Tr/2,Tr/2]
% .*((Dr>=0)&(Dr<=Tr));
%
end
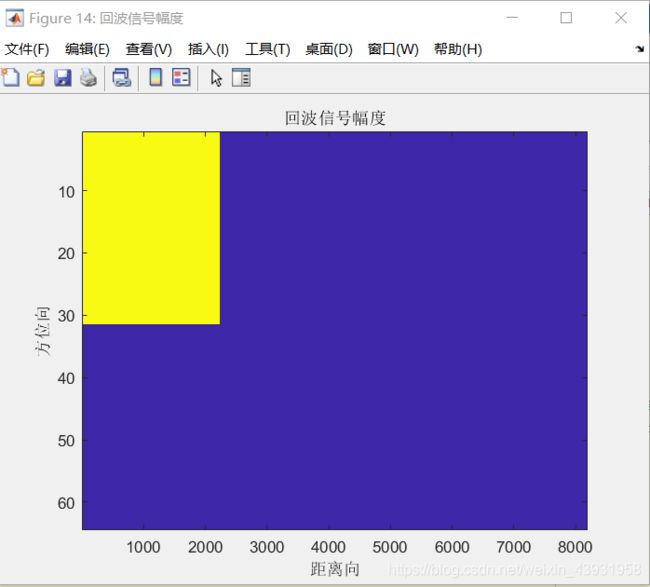
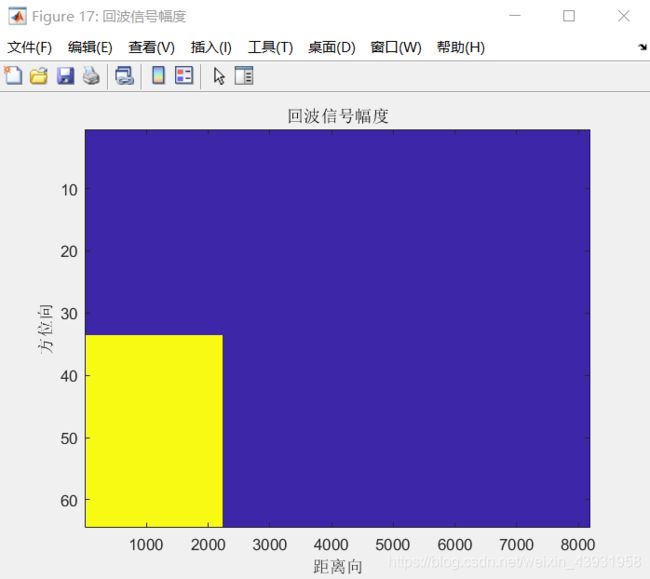
figure('Name','回波信号幅度');imagesc(abs(sig));
title('回波信号幅度');xlabel('距离向');ylabel('方位向');
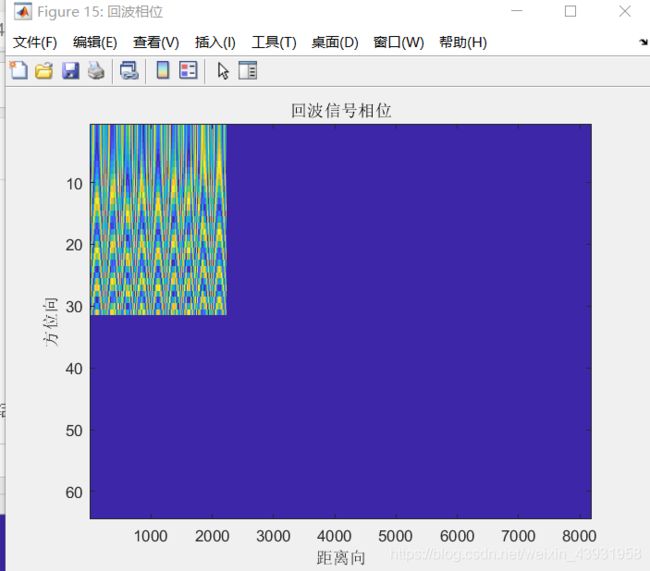
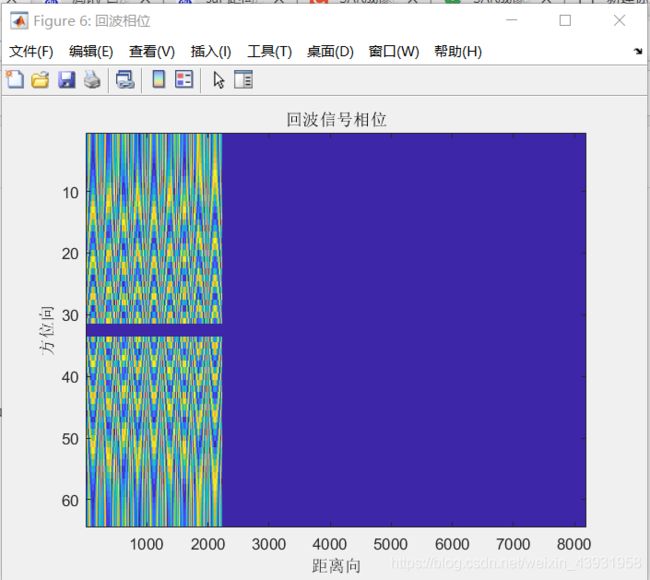
figure('Name','回波相位');imagesc(abs(angle(sig)));
title('回波信号相位');xlabel('距离向');ylabel('方位向');
%% BP成像
% 步骤一：距离向匹配滤波
sig_rd = fft(sig,[],2);
fr = -1/2:1/Nr:(1/2-1/Nr);
fr = fftshift(fr*Fr);
filter_r = ones(Na,1)*exp(j*pi*fr.^2/Kr);
sig_rd = sig_rd.*filter_r;
nup = 2;
Nr_up = Nr*nup;
nz = Nr_up - Nr;
dtr = 1/nup/Fr;
sig_rd_up = [sig_rd(:,1:Nr/2),zeros(Na,nz),sig_rd(:,(Nr/2+1):Nr)];
sig_rdt = ifft(sig_rd_up,[],2);
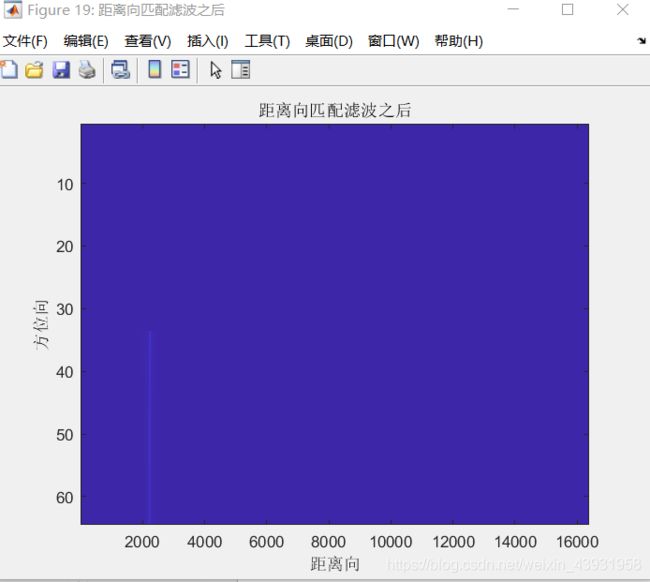
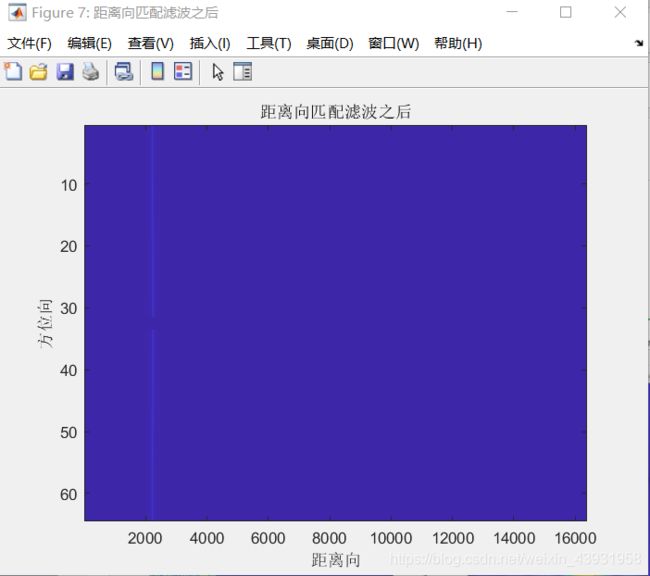
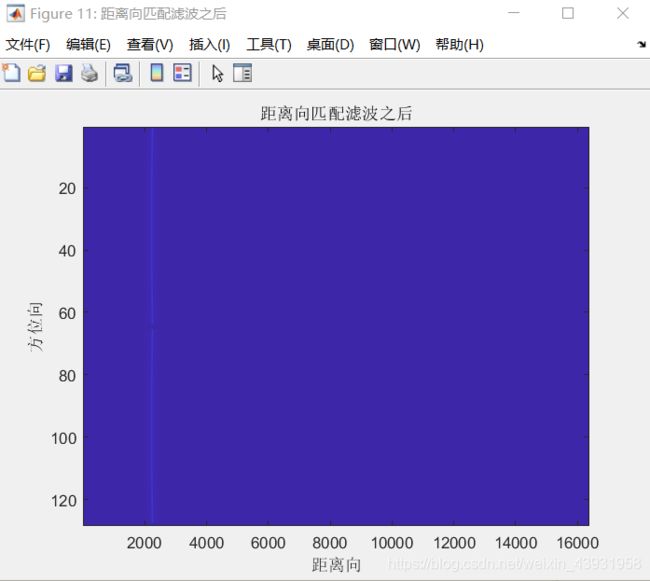
figure('Name','距离向匹配滤波之后');imagesc([],[],abs(sig_rdt));
title('距离向匹配滤波之后');xlabel('距离向');ylabel('方位向');
NN=32;
target_1 = target_analysis_1D_upsample( sig_rdt(:,2235-NN:2235+NN),Fr,Fa,Va);%调用target_analysis
%target_1 = target_analysis_1D_upsample( sig_rdt(:,14149-NN:14149+NN),Fr,Fa,Va);%调用target_analysis
%步骤二：对成像区域进行网格化
R = zeros(1,Nr);
for ii = 1:Nr
R(1,ii) = R_left + (R_right - R_left)/(Nr-1)*(ii-1);
end
R1 = ones(Na,1)*R;
Y = zeros(1,Na);
for ii = 1:Na
Y(1,ii) = Y_low + (Y_high - Y_low)/(Na-1)*(ii-1);
end
Y1 = Y'*ones(1,Nr);
%步骤三：根据时延在回波域寻找相应位置并进行成像
f_back = zeros(Na,Nr);
for ii = 1:Na
% R_ij = sqrt(R.^2 + (Y-0.5*a*ta(ii)^2).^2);
R_ij = sqrt(R1.^2 + (Y1-Va*ta(ii)).^2);
t_ij = 2*R_ij/c;
t_ij = round((t_ij - (2*Rmin/c - Tr/2))/dtr); %t_ij对应中心处，距离压缩后幅度最大的位置
it_ij = (t_ij>0 & t_ij<=Nr_up);
t_ij = t_ij.*it_ij + Nr_up*(1-it_ij);
sig_rdta = sig_rdt(ii,:);
sig_rdta(Nr_up) = 0;
f_back = f_back + sig_rdta(t_ij).*exp(1i*4*pi*R_ij/lamda);
end
figure('Name','BP算法处理后');imagesc(R,Y,abs(f_back));
title('BP算法处理后');xlabel('距离向');ylabel('方位向');
NN = 16;
% 分别得到每个点目标的切片放大；行切片、列切片；和相应的指标
% 目标1，点目标中心在 （（Naz/2+1），374）
target_1 = target_analysis( f_back((Na/2+1)-NN:(Na/2+1)+NN,374-NN:374+NN),Fr,Fa,Va);%调用target_analysis
（2）升采样函数 target_analysis_1D_upsample.m
function [PSLR_r,ISLR_r,IRW_r, PSLR_a,ISLR_a,IRW_a] = target_analysis_1D_upsample(s_ac,Fr,Fa,Vr)
% 补零方式很关键
% 这里采用的方法是逐行，逐列判断数据最小值位置，然后将在最小值位置处进行补零
% 输入变量： s_ac ——是需要进行指标分析的点目标点k，s_ac是它所在的一块矩阵数据。
% 输入变量： Fr —— 距离向采样率
% 输入变量： Fa —— 方位向采样率
% 输入变量： Vr —— 平台速度
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 取点目标中心 NN*NN 切片，进行升采样
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%
% 取点目标的中心切片，Na*NN
% 进行距离维升采样——如何进行一维升采样？？？
% 高频补零！！！！！——因此，判断哪里是高频，很重要！！
c = 3e8; % 光速
NN = 30; % 切片总长度，NN*NN
[row,column] = size(s_ac); % s_ac的矩阵大小
[bb,q] = max(max(abs(s_ac)));
column_max = q; % 二维矩阵最大值，所在第几列—— column_max。
s_ac_max = bb; % 矩阵最大值是—— x_max。
s_ac_test = s_ac(:,column_max-NN/2:column_max+NN/2-1);
% 得到Na*NN的切片
% 下面进行距离维升采样
S_ac_test_2 = fft(s_ac_test,[],2); % 距离向fft
% 接下来进行一维补零
S_ac_test_buling = zeros(row,32*NN);
% ====================================================================
% 利用for循环，在每行最小值的位置处补上7*NN的零，实现高频补零。
for pp = 1:row % 在每行的最小值位置补零
[C,I] = min(S_ac_test_2(pp,:));
S_ac_test_buling(pp,1:I) = S_ac_test_2(pp,1:I);
S_ac_test_buling(pp,32*NN-(NN-I)+1:32*NN) = S_ac_test_2(pp,I+1:NN);
end
% ====================================================================
s_ac_test = ifft(S_ac_test_buling,[],2);% 完成一维升采样
% 作图
figure;
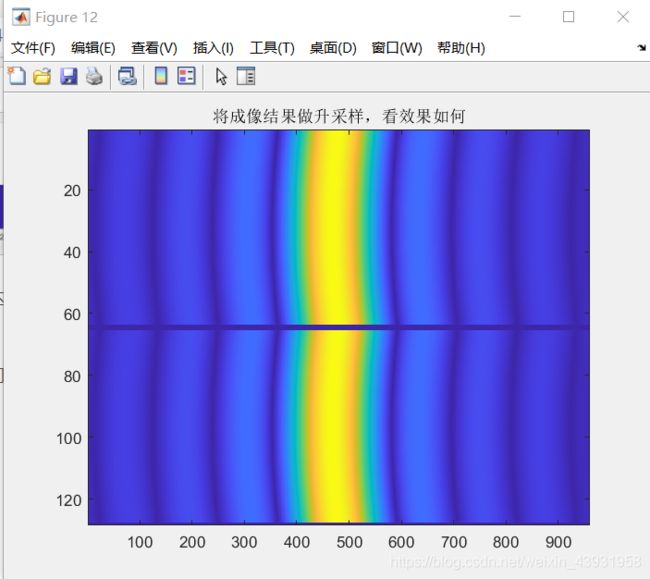
imagesc(abs(s_ac_test));
title('将成像结果做升采样，看效果如何');
8、其他一些距离压缩的结果
%近场条件下
Rpt = [R_near R_near+0.4 ]; % 点目标距离坐标
Ypt = [ 0 0 ]; % 点目标方位坐标
9、写在最后……
可能有一些同学会对升采样有些疑问，我说一下我的理解其实也就是在频域补了很多列零，然后频域采样点就倍数的增长，因为频域的采样点和时域的是相同的，因此也相当于对自己感兴趣的部分在时域进行了升采样。可以适用于已经完成了对数据的采集，但还想进一步看到在更多采样点下得到的目标的图像的样子。
但其实，这个地方也完全可以不要用到升采样，我想你们都想到了。对，直接在数据采样的时候增加采样点，以代码中的数据为例，
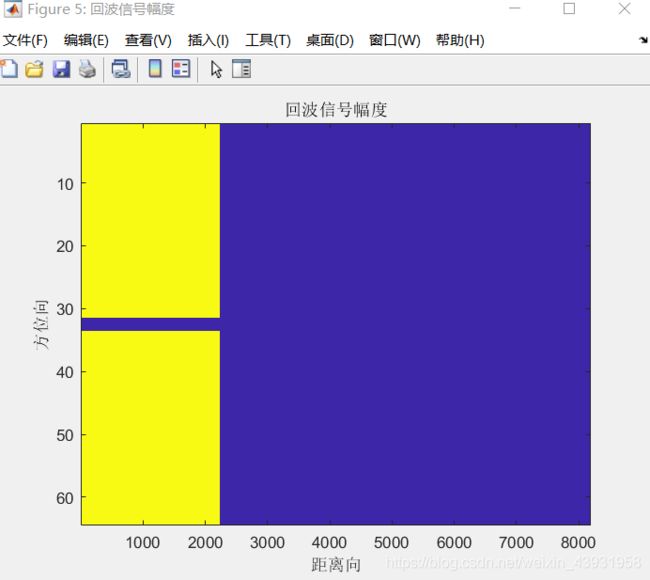
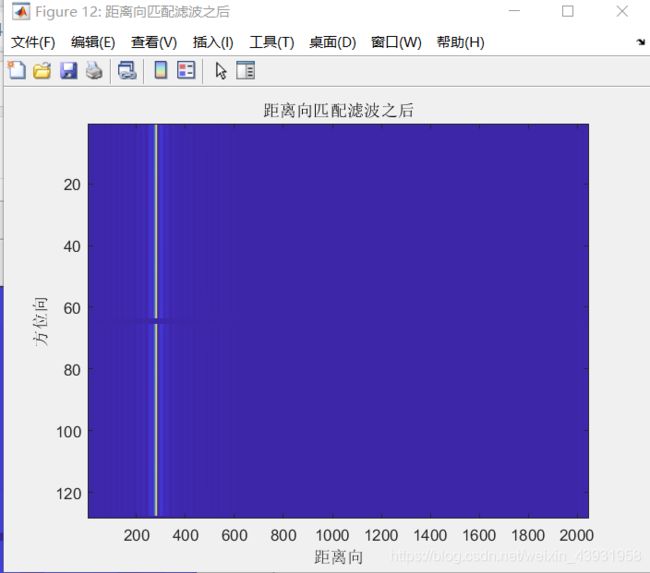
当距离带宽Br=50MHz时，采样频率Fr=1.2*B，根据我们所需要采样的时间范围，求得距离采样数Nr=1024。那么在采样点较为稀疏的情况下，相距较近的信号就混叠到同一距离门内，即看不出距离徙动现象了，如下图所示。
那我们可以通过增加带宽来提高采样点数，从而减小每一个距离门的大小，
当距离带宽Br=50GHz时，采样频率Fr=1.2*B，根据我们所需要采样的时间范围，求得距离采样数Nr=1024。那么在采样点较为稀疏的情况下，相距较近的信号就混叠到同一距离门内，即看不出距离徙动现象了，如下图所示。
