【聚类2】原型聚类

1. 原型聚类

概念

- "原型："
		"原型"是指样本空间中具有代表性的点。

- "别名："
		1）基于原型的聚类
		2）英文：prototype-based clustering

- "此类算法的原理："
		算法先对原型进行初始化，然后对原型进行迭代更新求解

- "常见的原型聚类算法："
		1. k均值算法(k-means)
		2. 学习向量量化(LVQ)
		3. 高斯混合聚类

算法讲解

1.1 k均值算法（K-Means）

1.1.1 最小化平方误差

$概念：$
           \ \ \ \ \ \ \ \ \ \ {}           $刻画了簇内样本围绕簇均值向量的紧密程度,值越小则簇内样本相似度越高$

$前提：$
           \ \ \ \ \ \ \ \ \ \ {}           $样本集D=\{x_1,x_2,...,x_m\}$

           \ \ \ \ \ \ \ \ \ \ {}           $簇划分C=\{C_1,C_2,...,C_k\}$

           \ \ \ \ \ \ \ \ \ \ {}           $簇C_i的均值向量：u_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$

$公式：$
           \ \ \ \ \ \ \ \ \ \ {}           $E={\sum }_{i=1}^k{\sum }_{x\in C_i}||x-u_i|{|}_2^2$

$最优解：$
           \ \ \ \ \ \ \ \ \ \ {}           $最小化E不好求：最优解需考察样本集所有可能的簇划分（NP问题）$
           \ \ \ \ \ \ \ \ \ \ {}           $NP问题：找一个解很困难，但验证一个解很容易（片面理解哈）$

$迭代法：$
           \ \ \ \ \ \ \ \ \ \ {}           $k均值算法采用了贪心策略，通过“迭代优化”来近似求解$

1.1.2 k均值算法伪代码

---

$输入：$
           \ \ \ \ \ \ \ \ \ \ {}           $样本集D=x_1,x_2,...,x_m$
           \ \ \ \ \ \ \ \ \ \ {}           $聚类簇数k$

$过程：$
           \ \ \ \ \ \ \ \ \ \ {}           $从D中随机选择k个样本作为初始均值变量u_1,u_2,...,u_k$

           \ \ \ \ \ \ \ \ \ \ {}           $repeat$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $令Ci=\varnothing (1\le i\le k)$

           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $forj=1,2,...,mdo$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $计算样本x_j与各均值向量u_i(1\le i\le k)的距离:d_{ji}=||x_j-u_i|{|}_2;$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $根据距离最近的均值向量确定x_j的簇标记:{\lambda }_j=mi{n}_{i\in \{1,2,...,k\}}{d}_{ji}$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $将样本x_j划入相应的簇:C_{{\lambda }_j}=C_{{\lambda }_j}\bigcup \{x_j\}$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $endfor$

           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $fori=1,2,...,kdo$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $计算新均值向量：u_i^{\prime }=\frac{1}{|C_i|}{\sum }_{x_i\in C_i}x$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $if{u}_i^{\prime }\ne u_{i}then$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $将当前均值向量u_i更新为u_i^{\prime }$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $else$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $保持当前均值向量不变$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $endif$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $endfor$

           \ \ \ \ \ \ \ \ \ \ {}           until
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           当前均值向量均未更新

$输出：$
           \ \ \ \ \ \ \ \ \ \ {}           簇划分C = {C1,C2,…,Ck}

---

• 1.1.3 k均值算法注意

- "最大运行轮数" + "最小调整幅度"
		1）为避免运行时间过长，通常设置一个"最大运行轮数"
		或"最小调整幅度"，
		2）若达到最大轮数或调整幅度小于阂值，则停止运行.

• 1.1.4 k-means聚类的缺点

- "2维k-means模型："
		1）以每个簇的中心为圆心，簇中点到簇中心点的欧氏距离最大值为半径画一个圆。
		2）k-means要求这些簇的形状必须是圆形的。
		3）k-means模型拟合出来的簇（圆形）与实际数据分布（可能是椭圆）差别很大。
		4）应用中缺少鲁棒性（在异常和危险情况下系统生存的能力）。

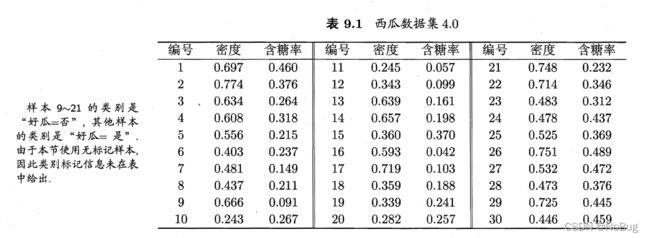
• 1.1.5 k均值算法例子

【D】

【k = 3】

【步骤】

$第一步：随机选择$
$算法开始时随机选取三个样本x_6,x_{12},x_{27}$
$即，u_1=(0.403;0.237),u_2=(0.343;0.099),u_3=(0.532;0.472)$

$第二步：考察样本$
$例：x_1=(0.697;0.460)$
$一般用欧式距离$
$d_1={\sum }_{i=1}^2||x_{1i}-u_{1i}|{|}_2$
$d_1=\sqrt{(0.697-0.403{)}^2+(0.460-0.237{)}^2}=0.369$
$d_2=\sqrt{(0.697-0.343{)}^2+(0.460-0.099{)}^2}=0.506$
$d_3=\sqrt{(0.697-0.532{)}^2+(0.460-0.472{)}^2}=0.166$
$因此x_1将划入簇C_3中$

$第三步：划分样本$
$C_1=\{x_5,x_6,x_7,x_8,x_9,x_{10},x_{13},x_{14},x_{15},x_{17},x_{18},x_{19},x_{20},x_{23}\}$
$C_2=\{x_{11},x_{12},x_{16}\}$
$C_3=\{x_1,x_2,x_3,x_4,x_{21},x_{22},x_{24},x_{25},x_{26},x_{27},x_{28},x_{29},x_{30}\}$

$第四步：更新均值向量$
$公式：u_i^{\prime }=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$
$u_1^{\prime }=\frac{1}{14}{\sum }_{x\in C_1}x$
$u_1^{\prime }=\frac{1}{14}\ast [(0.556;0.215)+(0.403;0.237)+(0.481;0.149)+(0.437;0.211)+(0.666;0.091)+(0.243;0.267)+(0.639;0.161)+(0.657;0.198)+(0.360;0.370)+(0.719;0.103)+(0.359;0.188)+(0.339;0.241)+(0.282;0.257)+(0.483;0.312)]=(0.473;0.214)$
$u_2^{\prime }=\frac{1}{3}{\sum }_{x\in C_2}x=(0.394,0.066)$
$u_3^{\prime }=\frac{1}{13}{\sum }_{x\in C_3}x=(0.623,0.388)$
$因为u_i^{\prime }\ne u^{\prime },所以更新均值向量$

$第五步：重复，当簇划分C_i相同时，停止$

1.2 学习向量量化

• 1.2.1 概念

"英文："
		Learning Vector Quantization,简称LVQ

"原理："
		1）与k均值算法类似，也是试图找到一组原型向量来刻画聚类结构
		2）LVQ假设数据样本带有类别标记，学习过程中利用这些监督信息来辅助聚类

"数学描述："
		给定样本集D={(x1,y1),...,(xm,ym)},
		每个样本(xj)，有n个属性描述的特征向量（xj1,xj2,...,xjn）,
		样本的标记(yj)。

"LVQ的目标："
		学得一组n维原型向量{p1,p2,...,pn},每个原型向量代表一个聚类簇，簇标记ti属于y

1.2.2 学习向量量化算法伪代码

---

$输入：$
           \ \ \ \ \ \ \ \ \ \ {}           $样本集D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$
           \ \ \ \ \ \ \ \ \ \ {}           $原型向量个数q,各原型向量预设的类别标记t_1,t_2,...,t_q$
           \ \ \ \ \ \ \ \ \ \ {}           $学习率\eta \in (0,1)$

$过程：$
           \ \ \ \ \ \ \ \ \ \ {}           $初始化一组原型向量\{p_1,p_2,...,p_q\}$
           \ \ \ \ \ \ \ \ \ \ {}           $repeat$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $从样本集D中随机选取样本(x_j,y_j)$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $计算样本x_j与p_i(1\le i\le q)的距离：dji=||x_j-p_i|{|}_2$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $找出与x_j距离最近的原型向量p_{i^{\ast }},i^{\ast }=argmi{n}_{i\in \{1,2,...,q\}}dji$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $if{y}_j=t_{i^{\ast }}then$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=p_{i^{\ast }}+\eta (x_j-p_{i^{\ast }})$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $else$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=p_{i^{\ast }}-\eta (x_j-p_{i^{\ast }})$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $endif$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $将原型向量p_{i^{\ast }}更新为p^{\prime }$
           \ \ \ \ \ \ \ \ \ \ {}           $until满足停止条件:最大轮转数或最小调整幅度$

$输出：$
           \ \ \ \ \ \ \ \ \ \ {}           $原型向量\{p_1,p_2,...,p_q\}$

---

• 1.2.3 学习向量量化算法注意

"原理："
		算法对原型向量进行迭代优化。
		   
"过程："
		1）在每一轮选代中，算法随机选取一个有标记训练样本。
		2）找出与其距离最近的原型向量。
		3）更新原型变量。
		
"更新原理："
		根据两者的"类别标记是否一致"来对原型向量进行相应的更新。

1.2.4 如何更新原型向量（原型向量更新原则）

$一、对样本x_j,若最近的原型向量p_{i^{\ast }}与x_j的类别标记相同,则让p_{i^{\ast }}向x_j的方向靠拢。$
           \ \ \ \ \ \ \ \ \ \ {}           $新原型向量：$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=p_{i^{\ast }}+\eta (x_j-p_{i^{\ast }}),$
           \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }与x_j之间的距离为：$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $||p^{\prime }-x_j|{|}_2=||p_{i^{\ast }}+\eta (x_j-p_{i^{\ast }})-x_j|{|}_2$
                  \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {}                              \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                         \ \ \ \ \ \ \ \ \ \ \ \ {}             $=(1-\eta )||p_{i^{\ast }}-x_j|{|}_2$
           \ \ \ \ \ \ \ \ \ \ {}           $令学习率\eta \in (0,1)：$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $则原型向量p_{i^{\ast }},在更新为p^{\prime }之后，将更接近x_j$
{}
{}
$二、对样本x_j,若最近的原型向量p_{i^{\ast }}与x_j的类别标记不同,则让p_{i^{\ast }}向x_j的方向远离。$
           \ \ \ \ \ \ \ \ \ \ {}           $新原型向量：$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=p_{i^{\ast }}-\eta (x_j-p_{i^{\ast }}),$
           \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }与x_j之间的距离为：$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $||p^{\prime }-x_j|{|}_2=||p_{i^{\ast }}+\eta (x_j-p_{i^{\ast }})-x_j|{|}_2$
                  \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {}                              \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                         \ \ \ \ \ \ \ \ \ \ \ \ {}             $=(1+\eta )||p_{i^{\ast }}-x_j|{|}_2$
           \ \ \ \ \ \ \ \ \ \ {}           $令学习率\eta \in (0,1)：$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $则原型向量p_{i^{\ast }},在更新为p^{\prime }之后，将更远离x_j$

• 1.2.5 Voronoi 剖分（Voronoi Tessellation）

$已知：$
           \ \ \ \ \ \ \ \ \ \ {}           $在学得一组原型向量\{p_1,p_2,...,p_q\}后，即可实现对样本空间X的簇划分$

$结论：$
           \ \ \ \ \ \ \ \ \ \ {}           $对任意样本x,它将被划入与其距离最近的原型向量所代表的簇中$

$换言之：$
           \ \ \ \ \ \ \ \ \ \ {}           $每个原型向量p_i定义了与之相关的一个区域R_i，$
           \ \ \ \ \ \ \ \ \ \ {}           $该区域中每个样本与p_i的距离不大于它与其他原型向量p_{i^{\prime }}(i^{\prime }\ne i)的距离。$

$数学描述：$
           \ \ \ \ \ \ \ \ \ \ {}           $R_i=\{x\in X|||x-p_i|{|}_2\le ||x-p_{i^{\prime }}|{|}_2,i^{\prime }\ne i\}$

$Voronoi剖分：$
           \ \ \ \ \ \ \ \ \ \ {}           $对样本空间X的簇划分\{R_1,R_2,...,R_q\},该划分通常称{为}^{\prime \prime }Voronoi剖{分}^{\prime \prime }$

• 1.2.6 学习向量量化算法例子

【D】

【q = 5】
即，学习目标找到5个原型向量$p_1,p_2,p_3,p_4,p_5$
令，其对应的类别标记分别为$c_1,c_2,c_3,c_4,c_5$

【$\eta =0.1$】

【步骤】

$第一步：原型向量随机初始化$
           \ \ \ \ \ \ \ \ \ \ {}           $根据样本的类别标记和簇的预设类别标记对原型向量进行随机初始化$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $假定初始化为样本：\{x_5,x_{12},x_{18},x_{23},x_{29}\}$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $对应的原型向量为：\{p_1,p_2,p_3,p_4,p_5\}$

$第二步：随机选取样本$
           \ \ \ \ \ \ \ \ \ \ {}           $例如：x_1=(0.697;0.460)$

$第三步：计算该样本与原型向量的距离$
           \ \ \ \ \ \ \ \ \ \ {}           $d_{1,5}=||x_1-x_5|{|}_2=\sqrt{(0.697-0.556{)}^2+(0.460-0.215{)}^2}=0.283$
           \ \ \ \ \ \ \ \ \ \ {}           $d_{1,12}=||x_1-x_{12}|{|}_2=0.506$
           \ \ \ \ \ \ \ \ \ \ {}           $d_{1,18}=||x_1-x_{18}|{|}_2=0.434$
           \ \ \ \ \ \ \ \ \ \ {}           $d_{1,23}=||x_1-x_{23}|{|}_2=0.260$
           \ \ \ \ \ \ \ \ \ \ {}           $d_{1,29}=||x_1-x_{29}|{|}_2=0.032$

$第四步：更新原型向量$
           \ \ \ \ \ \ \ \ \ \ {}           $LVQ更新p_5得到新原型向量$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=p5+\eta (x_1-p_5)$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=x_{29}+\eta (x_1-x_{29})$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=(0.725;0.445)+0.1\ast ((0.697;0.460)-(0.725;0.445))$
           \ \ \ \ \ \ \ \ \ \ {}                       \ \ \ \ \ \ \ \ \ \ {}           $p^{\prime }=(0.722;0.442)$

$第五步：重复操作，可以设置最大轮转数或最小幅度$

1.3 高斯混合聚类

• 1.3.1 概念

- "英文："
		1）Mixture-of-Gaussion cluster
		2）高斯混合模型：GMM

- "原理："
		1）与k均值，LVQ用原型向量来刻画聚类结构不同，
		2）高斯混合聚类采用概率模型来表达聚类原型。
		3）可以看做是k-means模型的一个优化。

- "涉及知识点："
		1）高斯分布
		2）贝叶斯公式
		3）极大似然法
		4）聚类

注：
	下面将简单介绍这些知识点。

1.3.2 高斯分布

a)概念：

- "高斯分布即正态分布"
		最熟知的就是："一元正态分布"

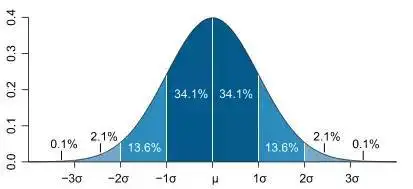
- "一元正态分布"
		1）曲线下的面积为1

b)指数函数：

$$exp(x):表示e的x次方$$

c)一元正态分布标准形式：

$$P(x)=\frac{1}{\sqrt{2\pi \sigma }}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$

d)一元正态分布曲线：

e)记作:

$$N(\mu ,{\sigma }^2)$$

f)二元高斯分布标准形式：

$$p(x)=\sum _{i=1}^n\frac{1}{2\pi }exp(-\frac{1}{2}{x}_i^2)$$

g)多元高斯分布的一般形式：

$$p(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$

$\mu$是n维均值向量
$\Sigma$是n$\times n$的协方差矩阵

1.3.3 贝叶斯公式

例子

假设，有三个箱子X、Y、Z，箱子里有红、黄、蓝色的球若干。
事 件 A ： 把 手 伸 向 一 个 箱 子 准 备 抽 取 球 。
事 件 B ： 从 某 个 箱 子 里 抽 出 一 个 球 。

概率乘法公式：

$$P(AB)=P(A)P(B|A)$$

$$P(B|A)：在事件A发生的前提下,事件B发生的概率$$

$$随机抽一个球，从Y箱抽到黄球的概率是多少?$$

全概率公式：

$$P(B)=P(A_1)P(B|A_1)+...+P(A_n)P(B|A_n)$$

$$P(B)=\sum _{i=1}^{n}P(A_i)P(B|A_i)$$

$$随机抽一个球，抽到黄球的概率是多少？$$

贝叶斯公式：

$$P(A_i|B)=\frac{P(A_i)P(B|A_i)}{{\sum }_{j=1}^{n}P(A_j)P(B|A_j)}$$

$$已知随机抽到黄球，求这个黄球是从Y箱的概率是多少？$$

$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}=\frac{P(AB)}{P(B)}$$

$P(B)为先验概率，表示每种类别分布的概率$
$P(B|A)为类条件概率，表示在某种类别前提下，某事发生的概率$
$P(A|B)为后验概率，表示某事发生了，并且它属于某一类别的概率$
$(后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。)$

1.3.4 概率密度函数（多元高斯分布的一般形式）

$前提：$
           \ \ \ \ \ \ \ \ \ \ {}           $对n维样本空间X中的随机向量x，若x服从高斯分布$

$公式：$
           \ \ \ \ \ \ \ \ \ \ {}           $P(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$

$解释：$
           \ \ \ \ \ \ \ \ \ \ {}           $u：n维均值向量$
           \ \ \ \ \ \ \ \ \ \ {}           $\Sigma ：n\times n协方差矩阵$

$记作：$
           \ \ \ \ \ \ \ \ \ \ {}           $P(x|\mu ,\Sigma )$
         \ \ \ \ \ \ \ \ {}         $（上述公式：更能表示与相应参数的依赖关系）$

1.3.5 高斯混合分布（全概率公式）

$公式：$
           \ \ \ \ \ \ \ \ \ \ {}           $PM(x)={\sum }_{i=1}^k{\alpha }_{i}P(x|{\mu }_i,{\Sigma }_i)$

$解释：$
           \ \ \ \ \ \ \ \ \ \ {}           $该分布共由k个混合成分组成，每个混合成分对应一个高斯分布。$
           \ \ \ \ \ \ \ \ \ \ {}           ${\alpha }_i>0为相应的混合系数，{\sum }_{i=1}^k{\alpha }_i=1$
           \ \ \ \ \ \ \ \ \ \ {}           ${\alpha }_i就是上文中的P(A_i),{\alpha }_i=P({\mu }_i,{\Sigma }_i)$

• 1.3.6 高斯混合聚类的步骤

第一步：原型样本的生成

（原型样本生成的过程由高斯混合分布给出：）
  首先，根据${\alpha }_1,...,{\alpha }_k$定义的先验分布选择高斯混合成分。
  然后，根据被选择的混合成分的概率密度函数进行采样。
  最终，生成相应的样本。

(举例：以训练集D = {$x_1,x_2,...,x_m$}为例：)

令,随机变量$z_j\in \{1,2,...,k\}$表示生成样本$x_j$的高斯回合成分。
得,$z_j$的先验概率P(B):
$$P(z_j=i)对应于{\alpha }_i(i=1,2,...,k)$$

再得,$z_j$的后验分布P(A|B)：
$$PM(z_j=i|x_j)=\frac{P(z_j=i)PM(x_j|z_j=i)}{PM(x_j)}$$
代换${\alpha }_i:$
$$PM(z_j=i|x_j)=\frac{{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{l=1}^k{\alpha }_{l}P(x_j|{\mu }_i,{\Sigma }_i)}$$
${\gamma }_{ji}:$
$$PM(z_j=i|x_j)就是样本x_j由第i个高斯混合成分生成的后验概率，简记：{\gamma }_{ji}$$

第二步：簇划分

当高斯混合分布已知时，高斯混合聚类将把样本集D划分为k个簇C={$C_1,C_2,...,C_k$}
每个样本$x_j$的簇标记${\lambda }_j:$
$${\lambda }_j=argmax{\gamma }_{ji},i\in \{1,2,...,k\}$$

最后：总结

从原型聚类的角度来看：
		1）高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画簇		
		2）划分则由原型对应的后验概率来确定。

1.3.7 极大释然估计

极大释然估计是什么？

    极大释然估计详解

1.3.8 高斯混合分布公式，模型参数$\{({\alpha }_i,{\mu }_i,{\Sigma }_i)|1\le i\le k\}$的求解

• 1.3.8.1 求解参数的总思想

给定样本集 D：
		1. 先采用极大似然估计，即最大化(对数)似然

		2. 再用EM算法，迭代优化，求解参数

• 1.3.8.2 最大化(对数)似然函数

$$LL(D)=ln(\prod _{i=1}^{m}PM(x_j))$$
$$=\sum _{j=1}^{m}ln(\sum _{i=1}^k{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i))$$

$符号“\prod ”是连乘符号$
${\prod }_{i=1}^k{\alpha }_i={\alpha }_1\ast {\alpha }_2\ast ...\ast {\alpha }_k$

• 1.3.8.3 EM算法迭代优化

首先：

$$1\le i\le k$$
$${\alpha }_i=P({\mu }_i,{\Sigma }_i)$$
$${\gamma }_{ji}=\frac{{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{l=1}^k{\alpha }_{l}P(x_j|{\mu }_i,{\Sigma }_i)}$$

第一步：$LL(D{)}_{{\mu }_i}^{\prime }=0$

$$\begin{array}{rl}LL(D{)}_{{\mu }_i}^{\prime }& =\frac{\partial LL(D)}{\partial {\mu }_i}\\ & =\sum _{j=1}^m[ln(\sum _{i=1}^k{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i)){]}_{{\mu }_i}^{\prime }\\ & =\sum _{j=1}^m\frac{{\sum }_{i=1}^k[{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i){]}_{u_i}^{\prime }}{{\sum }_{i=1}^k{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}\\ & =\sum _{j=1}^m\frac{{\sum }_{i=1}^k\{({\alpha }_i){}_{u_i}^{\prime }P(x_j|{\mu }_i,{\Sigma }_i)+{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i{)}_{{\mu }_i}^{\prime }\}}{{\sum }_{i=1}^k{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}\\ & =(最大化似然函数对{\mu }_i求导，好难，待续。直接看结果)\\ & =\sum _{j=1}^m\frac{{\alpha }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{l=1}^k{\alpha }_{l}P(x_j|{\mu }_l,{\Sigma }_l)}(x_j-{\mu }_i)=0\end{array}$$

第二步：简化

$$\begin{array}{rl}LL(D{)}_{{\mu }_i}^{\prime }& =\sum _{j=1}^m{\gamma }_{ji}(x_j-{\mu }_i)=0\end{array}$$

第三步：得${\mu }_i$

$${\mu }_i=\frac{{\sum }_{j=1}^m{\gamma }_{ji}{x}_j}{{\sum }_{j=1}^m{\gamma }_{ji}}$$

第四步：$LL(D{)}_{{\Sigma }_i}^{\prime }=0$

$$步骤待续$$

第五步：得${\Sigma }_i$

$${\Sigma }_i=\frac{{\sum }_{j=1}^m{\gamma }_{ji}(x_j-{\mu }_i)(x_j-u_i{)}^T}{{\sum }_{j=1}^m{\gamma }_{ji}}$$

第五步：得${\alpha }_i$

1.3.9 高斯混合聚类算法伪代码

• 1.3.10 高斯混合聚类例子

【样本集D】

【令高斯混合成分的个数 k = 3】

【步骤】