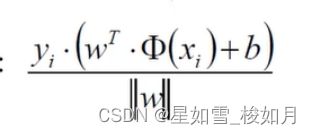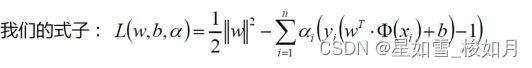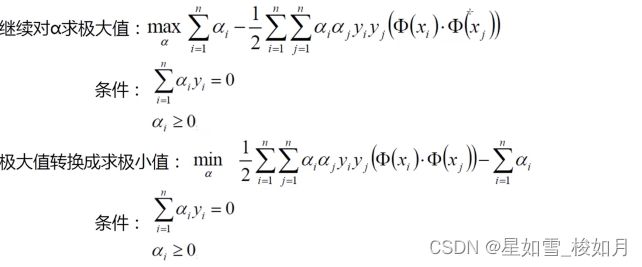梅科尔工作室-深度学习-SVM

目录

1.svm介绍

1.1.svm概念

1.2.svm与knn的对比

2.svm算法原理

2.1.距离计算

2.2.目标函数

2.3.软间隔优化

2.4.核函数

3.百度飞桨已有公开项目的展示

---

1.svm介绍

1.1.svm概念

        SVM（support vector machine）算法，即支持向量机算法，与knn算法同为分类算法，在深度学习出来之前，它以极大的优势（可以将数据升维，松弛变量等）在机器学习分类算法领域占很重要的地位。

        svm是一种二分法，将数据通过决策边界分为两类，当利用的是非线性核时，决策边界为非线性超曲面，而不是原始特征空间中的超平面。这个分类的边界形状由核决定。

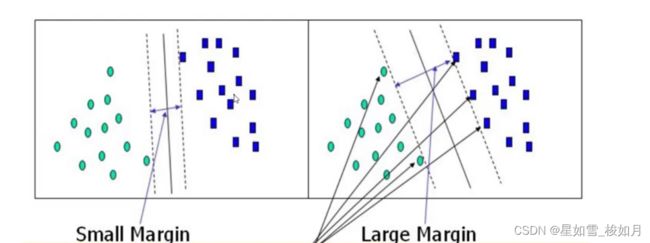
        而我们的目的是找到一条“线”，使得离它最近的数据离它最远。为什么要是离它最近呢？离它远的点对所求直线斜率w影响不大，推导时，离它最远的点对应阿尔法是0，在求w时没有影响，所以直线斜率与最近的点关系密切（这些点称为支持向量，用来”支撑“w的计算），这也是为什么算法叫”支持向量机“，w值只与那些支持向量有关，与离决策边界远的数据无关。为什么使离它最近的点离它最远呢？我们的目的是找到一个最大的margin，如果margin过小可能造成过拟合问题。

1.2.svm与knn的对比

（1）svm与knn一样，同为机器学习分类算法之一，目的是出现一个新数据时，能够根据原有数据将这个新来的数据分类。

（2）分类方式上，knn通过计算预测点与其他数据距离，给定一个k值，搜索离它最近的k个点，而这个数据的类别为这k个数据对应分类标签最多的类。而svm是一种二分法，它计算出一条决策边界将两类数据分为两类，当一个数据需要判断是什么类别时，根据这分成的两类判断。当是二维平面分类，数据为线上，线下；当是三维时，决策边界将整个空间分为两类。

（3）svm存在核概念，当数据在二维平面无法用线很好分割时，可以利用核将数据映射到三维空间，利用平面对数据分割，三维不行继续升维。根据推导过程，升维类比泰勒级数，理论上可以映射到无穷多维空间，但是维度越高，计算量提升也很快。升维的本质不是将数据升维，我们的数据在低维平面计算后，通过核函数将结果映射到高维，再找到决策边界。先将数据升维计算结果与先计算结果再升维效果是一样的。

2.svm算法原理

2.1.距离计算

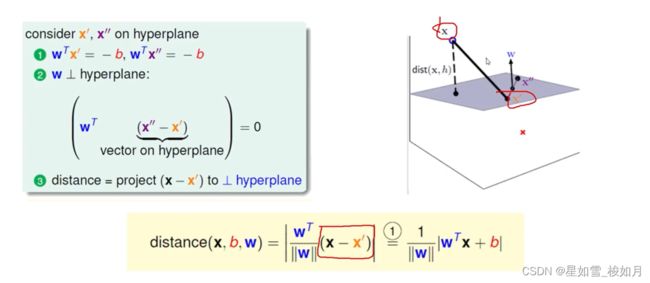
这里以三维平面点到平面距离举例。

         我们要求决策边界（超平面），首先假定超平面方程y = wx+b，设置阈值为0，大于0即wx+b>0为类别1这里用1表示，小于0用类别2这里用-1表示。这里x不单单是x，是向量，当维度高时，可以为矩阵。点到平面的距离可以用点与平面一点在平面单位法向量的投影表示，法向量是w，我们要知道方向，还要除以它的模。因为设置的阈值为0，wx‘在平面上根据定义的式子，它的值为-b。

        这里我们在乘以分类标签yi（1或-1），可以使整体的值大于零，当分类的值大于0时，标签1，相乘大于0。当分类值小于0，分类标签-1相乘大于零。这样我们的距离公式就可以去掉绝对值了。我们求的是距离（距离大于0）所以乘以分类标签，既可以让式子包含分类标签，也能保证计算结果为正值，一举两得。去了绝对值之后计算也会简化。

2.2.目标函数

我们要找到一个决策边界使得离他最近的点距他最远。

         从内部向外算min计算离他最近的点，max计算使这个点离决策边界最远。这里我们利用拉格朗日乘子法对我们所需的w与b进行求解。下面是我们的目标函数以及约束条件。

         在约束条件下，我们要求得我们的极值，这里我们就需要让原式分别对w与求偏导，当偏导等于0时，即为最值（有时候极值不满足条件，这个时候我们就要考虑边界问题）。 

 将求得极值对应的w与b带到原式（求拉格朗日乘子法的式子），得出以下式子。

然后对阿尔法求极大值，在原式子加个负号相当于求最小值。

 将阿尔法求出后带入求偏导的式子即可得出w的值，要说b的值怎么求，我们可以带一个点

y=wx+b，由w了，x与y也知道，b就求出了。

 2.3.软间隔优化

上面这些是在理想条件下计算的，但是我们的世界往往是不理想的，有的时候数据不能简简单单分开，比如一个数据直接跑到别人的领地，这样我们就需要设置松弛因子。你需要考虑这个是硬间隔还是软间隔，硬间隔宁愿margin小也要将结果分开，而软间隔选择舍弃一些噪声（异常数据）而求得最佳的margin（最宽）。

 看上式，当c很大时，后面松弛因子需要很小才能使式子受到的影响最小，当c很小时，当松弛因子大一点也没事，这样容错概率更高。c的选择要根据自己的想法，是否要舍弃一些数据换来更宽的margin。

2.4.核函数

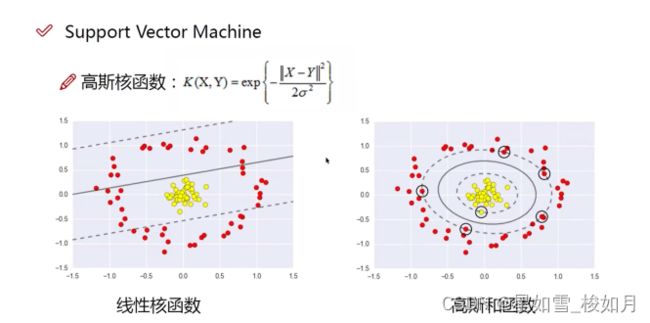
可以说svm与其他分类算法很大的优势之一是它有核函数。他可以将数据升维，可以解决非线性分类的问题。让线性不可分化为线性可分。如下图。

注意：我们一般不是将数据升维后一一进行计算这样计算量会很大，我们是在低维计算好后再通过核函数将结果映射到高维，计算结果不受影响（所以核函数很少）。

 核函数其实也不多。最常用的是高斯核函数

 3.百度飞桨已有公开项目的展示

利用百度飞桨上以及公开的项目

https://aistudio.baidu.com/aistudio/projectdetail/1931347

首先引入相关库文件。

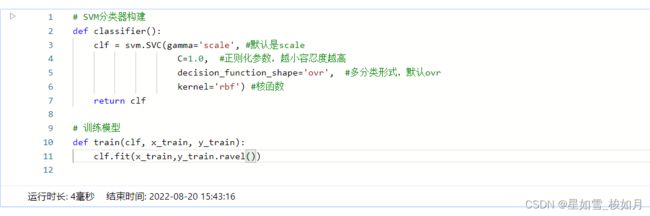
 对数据进行预处理。

 构建分类器、训练函数，初始化分类器实例、训练模型。

# 判断a与b是否相等
def show_accuracy(a, b, tip):
    acc = a.ravel() == b.ravel()
    print('%s Accuracy:%.3f' %(tip, np.mean(acc)))
    
# 分别打印训练集和测试集的准确率
def print_accuracy(clf, x_train, y_train, x_test, y_test):
    print('training prediction:%.3f' %(clf.score(x_train, y_train)))
    print('test data prediction:%.3f' %(clf.score(x_test, y_test)))
    # 原始结果和预测结果进行对比 predict() 表示对x_train样本进行预测,返回样本类别
    show_accuracy(clf.predict(x_train), y_train, 'traing data')
    show_accuracy(clf.predict(x_test), y_test, 'testing data')
    # 计算决策函数的值 表示x到各个分割平面的距离
    print('decision_function:\n', clf.decision_function(x_train))
    
def draw(clf, x):   
    iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width'
    # 开始画图
    x1_min, x1_max = x[:, 0].min(), x[:, 0].max()
    x2_min, x2_max = x[:, 1].min(), x[:, 1].max()
    # 生成网格采样点
    x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]  
    # 测试点
    grid_test = np.stack((x1.flat, x2.flat), axis = 1)
    print('grid_test:\n', grid_test)
    # 输出样本到决策面的距离
    z = clf.decision_function(grid_test)
    print('the distance to decision plane:\n', z)
    grid_hat = clf.predict(grid_test)
    # 预测分类值 得到[0, 0, ..., 2, 2]
    print('grid_hat:\n', grid_hat)
    # 使得grid_hat 和 x1 形状一致
    grid_hat = grid_hat.reshape(x1.shape)
    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
    
    plt.pcolormesh(x1, x2, grid_hat, cmap = cm_light) 
    plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark )
    plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolor='none', zorder=10 )
    plt.xlabel(iris_feature[0], fontsize=20) # 注意单词的拼写label
    plt.ylabel(iris_feature[1], fontsize=20)
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.title('Iris data classification via SVM', fontsize=30)
    plt.grid()
    plt.show()

# 模型评估
print('-------- eval ----------')
print_accuracy(clf, x_train, y_train, x_test, y_test)
# 模型使用
print('-------- show ----------')
draw(clf, x) 

 最终展示，展示准确率，可视化，评估模型准确度等。