几大排序算法(归并,快排,桶,堆,计数)
一、快速排序(工程使用最多) O(N*lgN) 递归
算法思想:重点在于划分,使得划分后左边部分全部小于右边,分治左右两部分,当两部分都有序后,就整体有序了
结果:小 → 大
static void QuickSort(int arr[],int p,int r){
if(p<r){ //最初 p为0 r为数组长度-1
int q = partition(arr,p,r); //划分 q是中间元素下标
// cout<
// for(int i=p;i<=r;i++) cout<
// cout<
QuickSort(arr,p,q-1); //递归对左半边进行快速排序
QuickSort(arr,q+1,r); //递归对左半边右边进行快排
}
}
用一个 partition方法得到中间元素的下标
static int partition(int arr[],int p,int r){
// if(r-p+1==2){
// if(arr[p]<=arr[r]) return r;
// else{
// swap(arr[p],arr[r]);
// return r;
// }
// }
int pivot = arr[p]; //pivot是主元 也叫作基准元素 ,拿他做比较的依据,如下
int sp = p+1;
int bigger = r;
while(sp<=bigger){
if(arr[sp]<=pivot){
sp++;
}else{
swap(arr[sp],arr[bigger]);
bigger--;
}
}
if(arr[p]>arr[bigger])swap(arr[p],arr[bigger]);
return bigger;
}
通过调用一次partition函数 使得数组得到一次遍历和挪动 , 在中间元素左边的 是<=它的,在中间元素右边的是比他大的元素。
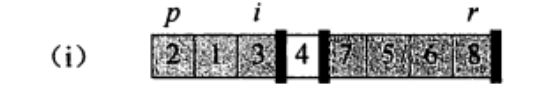
得到中间元素下标后
递归对左半边数组进行快速排序
递归对右半边数组进行快速排序
因为中间元素左边的都比他小或者相等,右边的都比他大,两边排序后自然就整体有序了
二、归并排序 O(N*lgN) 递归
算法思想:简单一分为二,重点在于合并。借用一辅助数组,两个指针指向两部分,谁小谁先走。
结果:小 → 大
static void MergeSort(int arr[],int p,int r){
if(p先递归后合并,合并时需要一个辅助数组
static void merge(int arr[],int p,int mid,int r){ //合并 也是排序的体现
// memcpy(help,arr+p,(r-p+1)*sizeof(int));//拷贝数组
for(int i=p;i<=r;i++) help[i] = arr[i];
// cout<<"help:";
// for(int i=p;i<=r;i++) cout<划分很简单 以 p+(r - p)/2 为中间元素下标 简单粗暴
划分好后,对左边数组(0,mid)递归进行归并排序
对右边数组(mid+1,r)递归进行归并排序
三、堆排序 O(N*lgN) 递归
算法思想:对于一个待排序数组,进行堆化,大顶堆或小顶堆都是把数组中的极值放在堆顶后,再与数组最后一个元素交换,交换后缩小堆化范围,重新进行堆化,当对化范围缩小至0后 排序停止。
结果:大顶堆堆化:小 → 大 小顶堆堆化:大 → 小
static void HeapSort(int arr[],int len){
if(len<=1) return; //如果数组长度<=1直接返回 不需排序
//大顶堆堆化
tomaxHeap(arr,n);
//交换
while(len>0){
swap(arr[0],arr[len-1]);
len--;
adjustHeap(arr,0,len);
}
}
从数组的 len/2 -1 下标开始 进行大顶堆堆化
static void tomaxHeap(int arr[],int n){
for(int i = n/2-1;i>=0;i--){ //为什么是n/2-1,因为二叉树的第n/2-1个节点是最后一个节点的父节点,最后一个节点要么是左节点要么是右节点,左节点父亲:(n-1)/2 右节点父亲: (n-2)/2
adjustHeap(arr,i,n); //大顶堆堆化
}
}
堆化好后,arr[0]要么是最大的,此时为大顶堆;要么是最小的,此时为小顶堆。将它与最后一个元素进行交换,交换后可能破坏大顶堆的性质,需要重新堆化,此时考虑范围缩小,不考虑最后一个元素,因为他已经是最大的了,现在要去找第二大的元素 放在堆顶。
static void adjustHeap(int arr[],int i,int len){
int maxindex = i; //最初默认指向父节点
//考虑越界
if(2*i +1 < len && arr[2*i+1]>arr[maxindex]) maxindex = 2*i+1;//有左孩子且比父节点大 ,maxindex指向左孩子
if(2*i +2 < len && arr[2*i+2]>arr[maxindex]) maxindex = 2*i+2;//有右孩子且比父节点大 ,maxindex指向右孩子
//此时maxindex指向最大值的下标
if(maxindex!=i){ //maxindex不等于父节点的话,说明这一小颗树不符合大顶堆性质,孩子比父亲大是小顶堆的特性,所以需要交换,并递归进行大顶堆判断
swap(arr[i],arr[maxindex]);
adjustHeap(arr,maxindex,len);
}
}
四、计数排序 O(N+K) N为原数组长度 K为原数组中元素最大值 非递归
算法思想:借用一个辅助数组存储原数组元素的出现次数。辅助数组的下标就是原数组的元素值,for循环从下标0开始扫描遇到值大于0的,就停下来覆盖原数组,扫描完后,元素组有序。
结果:小 → 大 (视辅助数组扫描方式而定)
static void CountSort(int a[],int len){
//先求数组最大值
int max = a[0];
for(int i=1;imax) max = a[i];
}
int help[max+1] = {0};//申请一块内存空间必须初始化!!!
for(int i=0;i0){
a[current++] = i; //覆盖
help[i]--;
}
}
}
以空间换时间
五、桶排序
算法思想:申请很多个 “桶” 也叫做 “容器”,这些桶是有序的。根据某种算法,将原数组的元素取出放在相应的桶中,分治思想,将每个桶进行排序后,依桶次取出。
结果:小 → 大
#include
#include
#include
using namespace std;
vector v[11]; //创建10个桶 第一个桶不要
static void f(int a[],int len){
for(int i=0;i>n;
int age[n] = {0};
for(int i=0;i>age[i];
f(age,n);
for(int i=0;i<11;i++){
vector::iterator iter = v[i].begin();
while(iter!=v[i].end()){
cout<<*iter<<' ';
iter++;
}
}
}
也是一种分治策略,因为直接对原数组进行排序 数据量大时间消耗大,把大问题拆解成一个个小问题,分别对小问题进行处理后 大问题就解决了,这种方式也是能节省一点时间的。跟希尔排序分组有异曲同工之处
图片来自 https://www.cnblogs.com/maluning/p/7944809.html#4176114
