图像处理(十一):轮廓检测
图像处理笔记总目录
1 图像的轮廓
轮廓可以简单认为成将连续的点(连着边界)连在一起的曲线,具有相同的颜色或者灰度。轮廓是图像目标的外部特征,这种特征对于我们进行图像分析,目标识别和理解等更深层次的处理都有很重要的意义。
轮廓提取的基本原理:对于一幅背景为黑色、目标为白色的二值图像,如果在图中找到一个白色点,且它的8邻域(或4邻域)也均为白色,则说明该点是目标的内部点,将其置为黑色,视觉上就像内部被掏空一样;否则保持白色不变,该点是目标的轮廓点。一般在寻找轮廓之前,都要将图像进行阈值化或Canny边缘检测,转换为二值化图像。
在这里我们看下边缘检测和轮廓检测的区别:
边缘检测主要是通过一些手段检测数字图像中明暗变化剧烈(即梯度变化比较大)像素点,偏向于图像中像素点的变化。如canny边缘检测,结果通常保存在和源图片一样尺寸和类型的边缘图中。
轮廓检测指检测图像中的对象边界,更偏向于关注上层语义对象。如OpenCV中的findContours()函数, 它会得到每一个轮廓并以点向量方式存储,除此也得到一个图像的拓扑信息,即一个轮廓的后一个轮廓、前一个轮廓等的索引编号。
1.1 查找轮廓
在OPenCV中查找轮廓的API:contours, hierarchy = cv2.findContours(img, mode, method)
参数:
- img: 输入图像,二值图
- mode: 轮廓的检索模式,主要有四种方式:
- cv2.RETR_EXTERNAL:只检测外轮廓,所有子轮廓被忽略
- cv2.RETR_LIST:检测的轮廓不建立等级关系,所有轮廓属于同一等级
- cv2.RETR_CCOMP:返回所有的轮廓,只建立两个等级的轮廓。一个对象的外轮廓为第 1 级组织结构。而对象内部中空洞的轮廓为 第 2 级组织结构,空洞中的任何对象的轮廓又是第 1 级组织结构。
- cv2.RETR_TREE:返回所有的轮廓,建立一个完整的组织结构的轮廓。
- method:轮廓的近似方法,主要有以下两种:
返回:
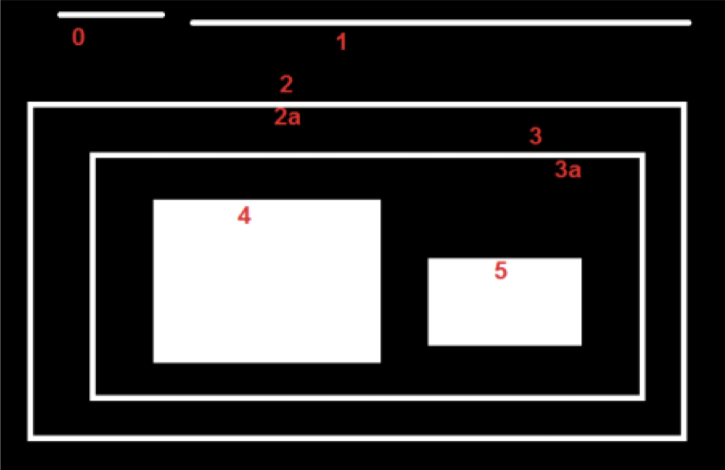
在这幅图像中,我给这几个形状编号为 0-5。2 和 2a 分别代表最外边矩形的外轮廓和内轮廓。
在这里边轮廓 0,1,2 在外部或最外边。我们可以称他们为 0 级,简单来说就是他们属于同一级,接下来轮廓 2a,把它当成轮廓 2 的子轮廓。它就成为第 1 级。轮廓 3 是轮廓 2a 的子轮廓,成为第 3 级。轮廓 3a 是轮廓 3 的子轮廓,成为第 4 级,最后轮廓 4,5 是轮廓 3a 的子轮廓,成为5级,这样我们就构建的轮廓的层级关系。
我们再回到返回值中,不管层次结构是什么样的, 每一个轮廓都包含自己的信息。hierarchy使用包含四个元素的数组来表示:
[Next,Previous, First_Child,Parent]
其中:
-
Next 表示同一级组织结构中的下一个轮廓,
以上图中的轮廓 0 为例,轮廓 1 就是他的 Next。同样,轮廓 1 的 Next 是 2,Next=2。 那轮廓 2 呢?在同一级没有 Next。这时 Next=-1。而轮廓 4 的 Next 为 5,所以它的 Next=5。
-
Previous 表示同一级结构中的前一个轮廓。
轮廓 1 的 Previous 为轮廓 0,轮廓 2 的 Previous 为轮廓 1。轮廓 0 没有 Previous,所以 Previous=-1。
-
First_Child 表示它的第一个子轮廓。
轮廓 2 的子轮廓为 2a。 所以它的 First_Child 为 2a。那轮廓 3a 呢?它有两个子轮廓。但是我们只要第一个子轮廓,所以是轮廓 4(按照从上往下,从左往右的顺序排序)。
-
Parent 表示它的父轮廓。
与 First_Child 刚好相反。轮廓 4 和 5 的父轮廓是轮廓 3a。而轮廓 3a 的父轮廓是 3。
注意: 如果轮廓没有父轮廓或子轮廓时,则将其置为-1。
1.2 绘制轮廓
我们查找到图像中的轮廓后,怎么将他绘制在图像上呢?
cv2.drawContours(img, contours, index, color, width)
参数:
- img:轮廓检测的原图像
- contours:检测出的轮廓。
- Index:轮廓的索引,绘制单个轮廓时指定其索引,绘制全部的轮廓时设为-1即可。
- color和width:绘制时轮廓的颜色及线型的宽度。
示例:
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 1 图像读取
img = cv2.imread('../image/beijing.jpg')
imgray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 2 边缘检测
canny = cv2.Canny(imgray, 127, 255, 0)
# 3 轮廓提取
contours, hierarchy = cv2.findContours(canny, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
# 4 将轮廓绘制在图像上
img = cv2.drawContours(img, contours, -1, (0, 0, 255), 2)
# 5 图像显示
plt.imshow(img[:, :, ::-1])
plt.xticks([]), plt.yticks([])
plt.show()
2 轮廓的特征
在提取了图像的轮廓后,可以计算轮廓的不同特征,我们现在主要看下:轮廓的面积,周长,边界框等。
2.1 轮廓面积
轮廓面积是轮廓所包围的区域的面积,在OpenCV中使用的API是:area = cv2.contourArea(cnt)
2.2 轮廓周长
轮廓周长也被成为弧长,在OpenCV中使用的API是:perimeter = cv2.arcLength(cnt,isclosed)
2.3 轮廓近似
轮廓近似是将轮廓形状近似为到另外一种由更少点组成的轮廓形状,新轮廓的点的数目由我们设定的准确度来决定。
假设我们要在一幅图像中查找一个矩形,然而这个图凹凸不平,直接提取轮廓无法提取到一个完美的矩形。因此我们就可以使用轮廓近似函数来近似这个形状了。
API:approx = cv.approxPolyDP(cnt,epsilon,isclosed)
参数:
- cnt:要进行轮廓近似的原始轮廓
- epsilon:从原始轮廓到近似轮廓的最大距离,是一个准确度参数,该参数对调整后的结果很重要。
- Isclosed:指定轮廓是否闭合
返回:
- approx:返回的点集,绘制时将其连接起来绘制最终的近似轮廓。
示例:
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 1 图像读取
img = cv2.imread('../image/rec.png')
imgray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 2 转换为二值图
ret,thresh = cv2.threshold(imgray,127,255,0)
# 3 轮廓提取
contours, hierarchy = cv2.findContours(thresh,cv2.RETR_LIST,cv2.CHAIN_APPROX_NONE)
# 4 轮廓近似
epsilon = 0.1*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
# 5 将轮廓绘制在图像上
# 5.1 原始轮廓
img1 = img.copy()
img1 = cv2.drawContours(img1, contours, -1, (0,0,255), 2)
# 5.2 轮廓近似后的结果
img2 = img.copy()
img2 = cv2.polylines(img2, [approx], True, (0, 0, 255), 2)
# 6 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img1[:,:,::-1]),plt.title('轮廓检测结果')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img2[:,:,::-1]),plt.title('轮廓近似后结果')
plt.xticks([]), plt.yticks([])
plt.show()
2.4 凸包
凸包是计算机几何图形学中的概念,简单来说,给定二维平面点集,凸包就是将最外层的点连接起来构成的凸多边形,他能够包含物体中所有的点。物体的凸包常应用在物体识别,手势识别及边界检测等领域。
在OpenCV中检测凸包的API是:hull = cv2.convexHull(points, clockwise, returnPoints)
参数:
- points:传入的轮廓
- clockwise:方向标志。如果设置为 True,输出的凸包是顺时针方向的。 否则为逆时针方向
- returnPoints:默认值为 True。它会返回凸包上点的坐标。 如果设置 为 False,就会返回与凸包点对应的轮廓上的点的索引。
返回:
- hull: 输出的凸包结果
示例:
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 1 图像读取
img = cv2.imread('../image/star 2.jpeg')
img1 =img.copy()
imgray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 2 边缘检测
canny = cv2.Canny(imgray,127,255,0)
# 3 轮廓提取
contours, hierarchy = cv2.findContours(canny,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)
# 4 将轮廓绘制在图像上
img = cv2.drawContours(img, contours, 1, (255,0,0), 2)
# 5 凸包检测
hulls=[]
for cnt in contours:
# 寻找凸包使用cv2.convexHull(contour)
hull = cv2.convexHull(cnt)
hulls.append(hull)
draw_hulls = cv2.drawContours(img1,hulls, -1, (0, 255, 0), 2)
# 5 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('轮廓检测结果')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(draw_hulls[:,:,::-1]),plt.title('凸包结果')
plt.xticks([]), plt.yticks([])
plt.show()
2.5 边界矩形
轮廓检测中的边界矩形有两种,一种是直边界矩形,一种是旋转边界矩形,分别介绍如下:
直边界矩形 :一个直矩形,没有进行旋转。它不会考虑对象是否旋转,所以该边界矩形的面积不是最小的。可以使用函数cv2.boundingRect()查找得到。
x,y,w,h = cv2.boundingRect(cnt)
img = cv2.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)
返回值中,(x,y)是矩阵左上角的坐标,(w,h)是举行的宽和高。
旋转边角矩形:这个边界矩形是面积最小的,他考虑了对象的旋转。用函数cv2.minAreaRect(),返回的是一个Box2D结构,其中包含矩形中心点的坐标(x,y),以及矩形的宽和高(w,h),以及旋转角度。但是要绘制这个矩形需要矩形的4个角点。可以通过函数cv2.boxPoints()获得。
s = cv2.minAreaRect(cnt)
a = cv2.boxPoints(s)
a = np.int0(a)#必须转换a的类型为int型
cv2.polylines(im,[a],True,(0,0,255),3)
示例:
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 1 图像读取
img = cv2.imread('../image/arrows.jpg')
imgray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 2 转换为二值图
ret,thresh = cv2.threshold(imgray,127,255,0)
# 3 轮廓提取
contours, hierarchy = cv2.findContours(thresh,1,2)
# 4 将轮廓绘制在图像上
img = cv2.drawContours(img, contours, 1, (0,0,255), 2)
cnt = contours[1]
# 5 边界矩形
# 5.1 直边界矩形
x,y,w,h = cv2.boundingRect(cnt)
img = cv2.rectangle(img,(x,y),(x+w,y+h),(0,255,0),3)
# 5.2 旋转边界矩形结果
s = cv2.minAreaRect(cnt)
a = cv2.boxPoints(s)
a = np.int0(a)#转换a的类型为int型
cv2.polylines(img,[a],True,(0,0,255),3)
# 6 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('矩形结果')
# plt.xticks([]), plt.yticks([])
plt.show()
2.6 最小外接圆
最小外接圆是对象的外切圆,它是所有包含目标对象的圆中面积最小的一个,我们使用函数cv2.minEnclosingCircle()获取最小外接圆。
将上述案例中的边界矩形的代码改为如下所示,即可检测对象的最小外接圆
(x,y),radius = cv2.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
img = cv2.circle(img,center,radius,(0,255,0),2)
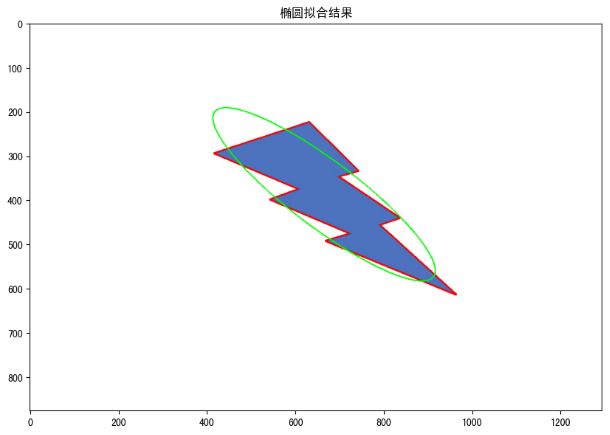
2.7 椭圆拟合
椭圆拟合法的基本思路是:对于给定平面上的一组样本点,寻找一个椭圆,使其尽可能接近这些样本点。也就是说,将图像中的一组数据以椭圆方程为模型进行拟合,使某一椭圆方程尽量满足这些数据,并求出该椭圆方程的各个参数。
就椭圆拟合而言,就是先假设椭圆参数,得到每个待拟合点到该椭圆的距离之和,也就是点到假设椭圆的误差,求出使这个和最小的参数。
在OPenCV中我们使用cv2.ellipse()来进行椭圆拟合,将边界矩形中的代码改为如下所示,就可得到椭圆拟合的结果:
ellipse = cv2.fitEllipse(cnt)
img = cv2.ellipse(img,ellipse,(0,255,0),2)
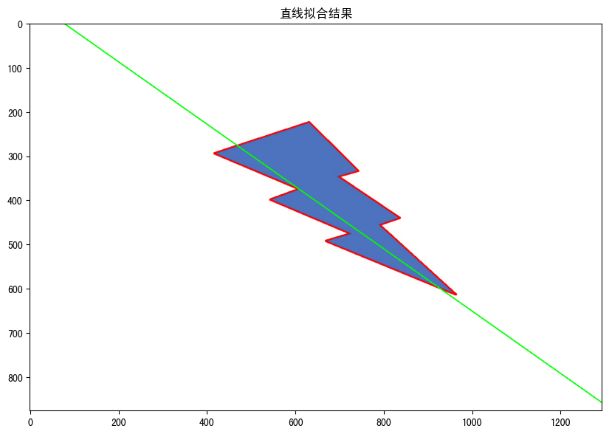
2.8 直线拟合
直线拟合就是将图像中的对象拟合成一条直线过程,在OPenCV中拟合直线的API是:output = cv2.fitLine(points, distType, param, reps, aeps)
参数:
- points:待拟合直线的点的集合,可以是检测处理轮廓结果
- distype:距离公式,在进行拟合是,要使输入点到拟合直线的距离之和最小,常用的用以下几种:
- cv2.DIST_L1:曼哈顿距离
- cv2.DIST_L2:欧式距离
- cv2.DIST_C:切比雪夫距离
- param:距离参数,可以设为0
- Reps,aeps:用于表示拟合曲线所需要的径向和角度精度,通常设为0.01
返回:
- output:[vx,vy,x,y]的1*4 的数组,前两个表示直线的方向,即vy/vx表示斜率,后两位表示直线上的一个点。
将边界矩形中的代码改为如下示,即可进行直线拟合:
rows,cols = img.shape[:2]
[vx,vy,x,y] = cv2.fitLine(cnt, cv2.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
im = cv2.line(img,(cols-1,righty),(0,lefty),(0,255,0),2)