【路由优化】基于matlab随机搜索算法优化带有速度的路由网络【含Matlab源码 2046期】

一、随机搜索算法简介

1 随机搜索算法
原始随机搜索方法的提法为:设f(θ)为待优化的目标函数,θ为在状态空间中的当前点(待估参数向量),通过以下四步迭代运算,试图找到最优解θ*。

步骤1:选取初始点θ作为当前点,计算f(θ)。

步骤2:在参数空间中,给当前的θ加上一个随机向量dθ,并计算新点θ+dθ处的目标函数值。

步骤3:如果f(θ+dθ)＜f(θ),则令当前θ等于θ+dθ;如果f(θ-dθ)＜f(θ),令当前θ等于θ-dθ。

步骤4:如果已经达到最大迭代计算次数或者前后相邻两次搜索的目标函数值的相对误差或绝对误差小于给定的数值,则停止运算,输出计算结果。否则,返回步骤2,寻找新的点。

由于上述算法的搜索方向完全由随机数发生器确定,所以这是一个真正的随机方法,在文中我们称其为原始随机搜索算法,图1给出了原始随机搜索算法的流程图。

二、部分源代码

clc;
clear all;
close all;

global Qk ax ay Dik tou beta indA indB

%% Intialization
Nnodes=1;
Emax=1000;
Emin=5;
nk=8;
V=20;
Ra=10+(100-10).*rand(1,nk); % data rate
%% New
T=50; %patrolling cycle time constraint
% v,a—velocity and accelration
%% Charging behavior eqn 1
Ptx=10;
Gtx=3;
Grx=2;
lamda=20e-3;
Lp=0.3;
eta=0.9;
beta=0.2316;

tou= ((Gtx.*Grx.eta./Lp).(lamda./4.*pi).^2).*Ptx
% Distance4 bw node and chaerger
d=10; %— Modified

Prx=@(d)(tou./(d+beta).^2)

Prx(2)
% Tx power of Charger

D=15;
itr=5;
for i1=1:itr

noOfNodes=nk;
figure(1);
axis tight manual
clf;
hAx1 = axes;
hold on;

a=1;
b=nk;
r =floor( a + (b-a).*(rand(2,1)));

while(r(1)==r(2))
r =floor( a + (b-a).*(rand(2,1)));
end
sor =r(1);%source node
des=r(2);%destination node
R =5.5; %node transmission range
a=1;
b=noOfNodes;
%X=floor(a + (b-a).*rand(1,noOfNodes));
%Y=floor(a + (b-a).*rand(1,noOfNodes));
X = 1+(30-1)*rand(1,nk);
Y = 1+(30-1)*rand(1,nk);

X1= 10+(20-10)*rand(1,1);
Y1= 10+(20-5)*rand(1,1);
%
X2= 5+(15-5)*rand(1,1);
Y2= 10+(10-5)*rand(1,1);

%Z =[1 0.1 0.6 0.8 0.6 0 0.1 1 1 1];

%plotting network topology
%i2=1;
for i2 = 1:noOfNodes
plot(X(i2),Y(i2),‘o’,‘LineWidth’,1,…
‘MarkerEdgeColor’,‘k’,…
‘MarkerFaceColor’,‘y’,…
‘MarkerSize’,8’);
xlabel(‘X in m’)
ylabel(‘Y in m’)
text(X(i2), Y(i2), num2str(i2),‘FontSize’,10);

%% Destination
  plot(X2,Y2,'^','LineWidth',1,...
          'MarkerEdgeColor','k',...
          'MarkerFaceColor','r',...
          'MarkerSize',14'); 

hold on

end

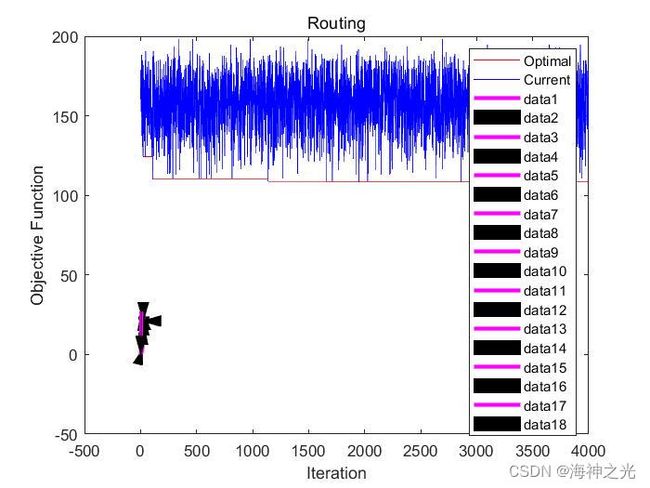
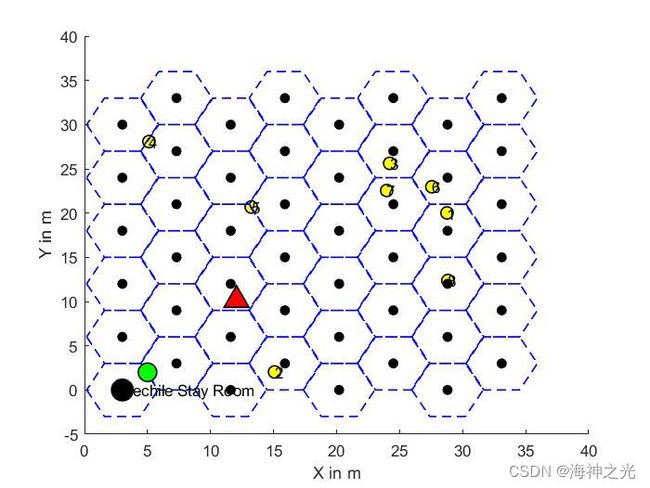
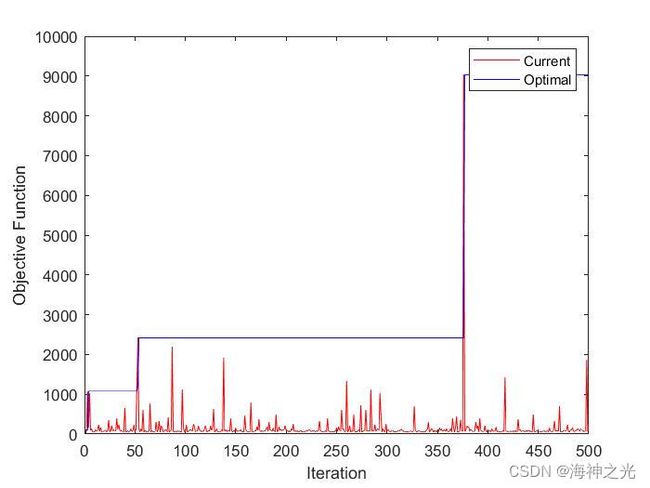
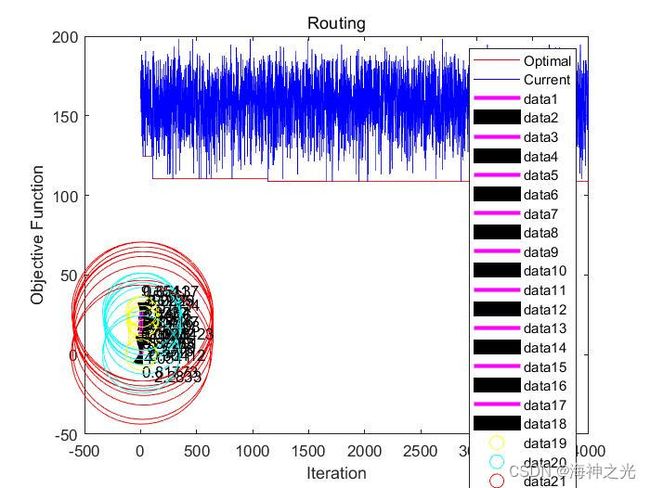
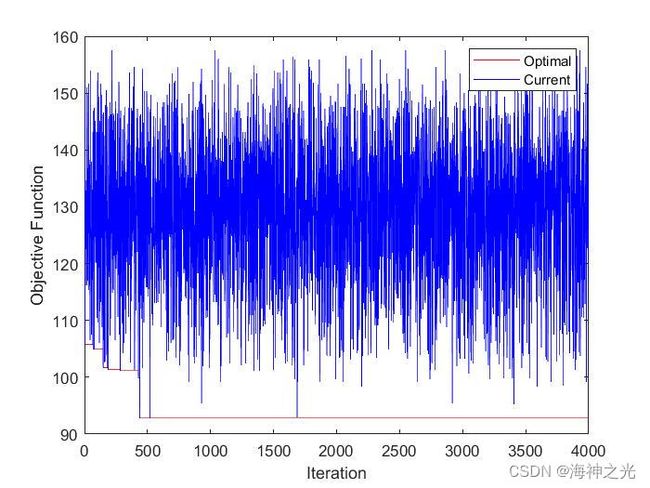
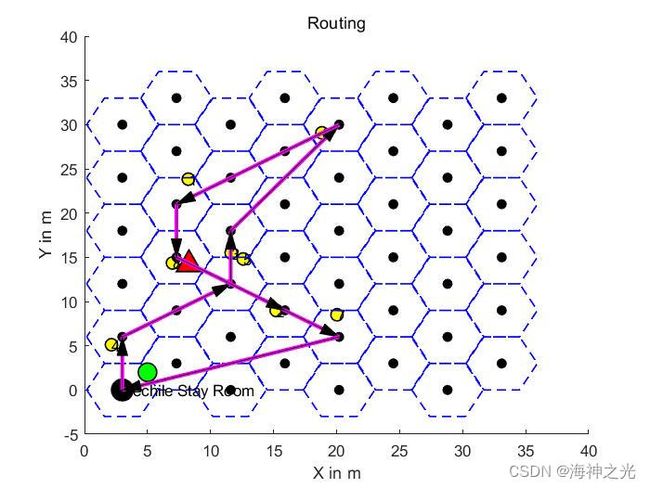
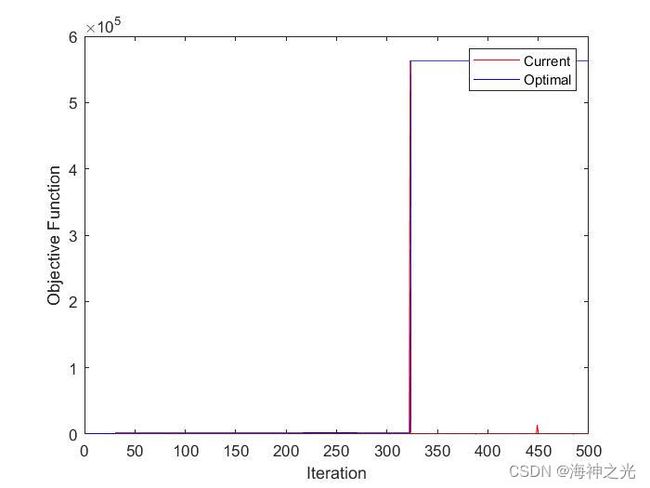
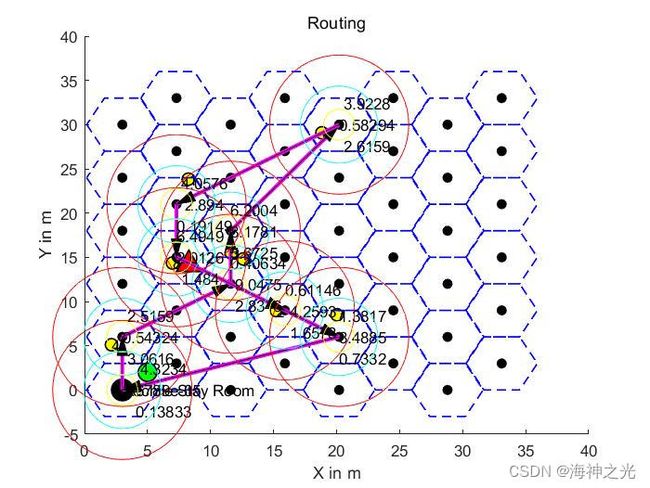
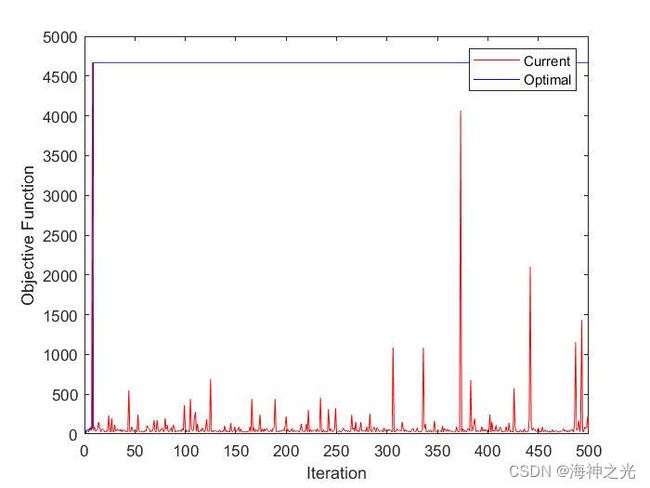
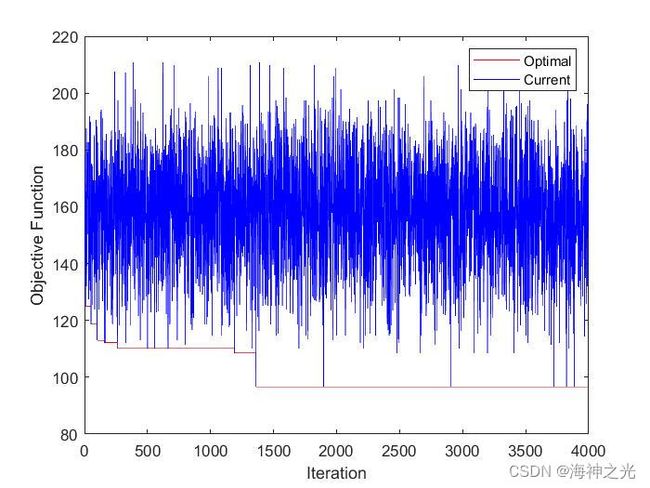
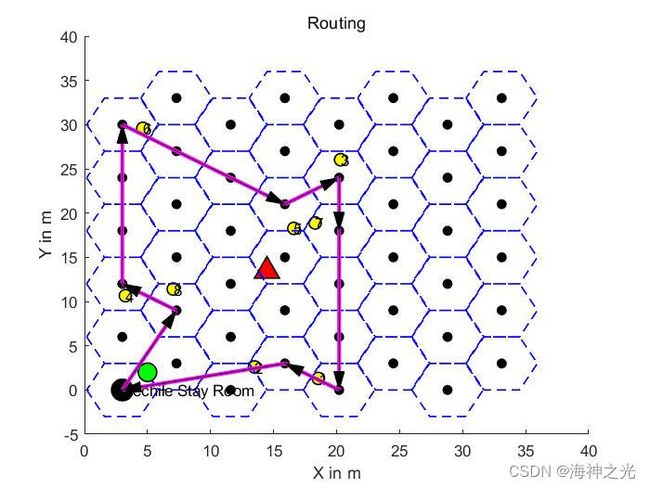
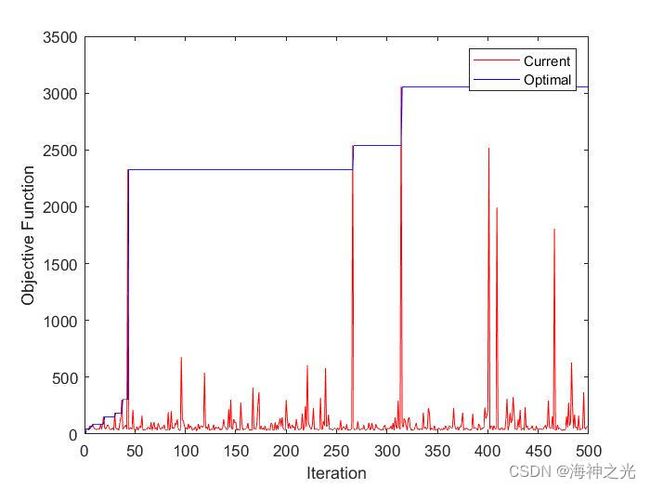
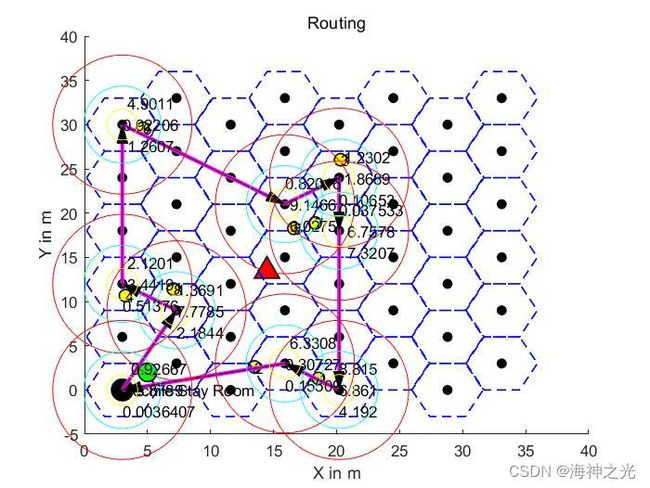
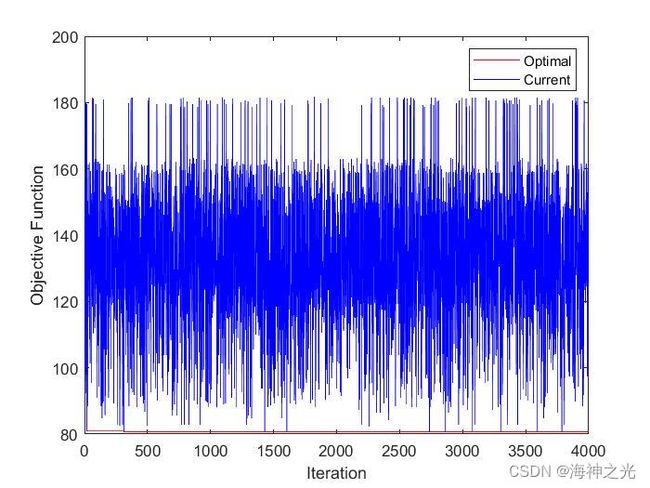
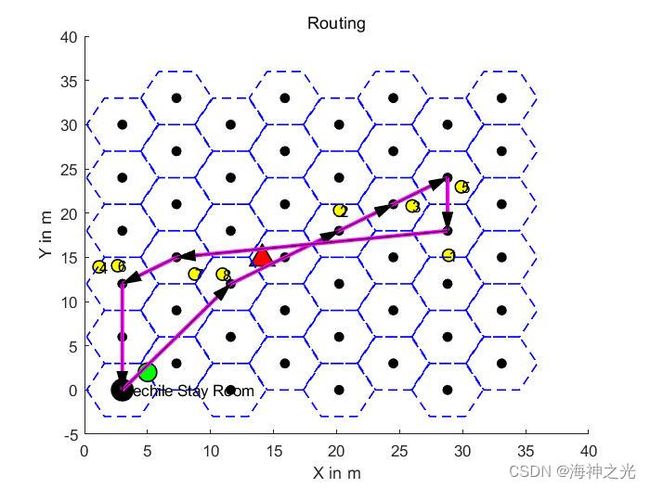
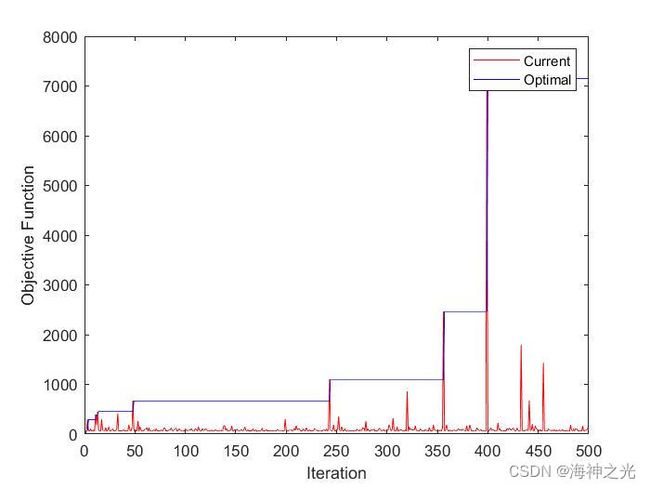
三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]郭建青,周宏飞,李彦,王洪胜.随机搜索算法在确定河流水质参数中的应用[J].水文. 2010,30(02)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除