FPGA学习记录(5)<低通&带通FIR滤波器FPGA实现>
目录
-
- Matlab仿真低通的FIR滤波器BLACKMAN窗并使用FPGA实现
-
- (1)FIR&IIR介绍
- (2)FIR的FPGA实现与matlab仿真(FIR&BLACKMAN窗&4MHz采样&低通滤波):
-
- ①采用Matlab中的FDA插件设计滤波器
- ②FDA导出滤波器系数
- ③根据滤波器的量化系数使用FPGA代码实现
-
- step 1:建立好相关的工程文件(FIR_low8.v以及对应的tb文件)
- step 2:Verilog代码书写
- step 3:生成待滤波波形,并且使用matlab对波形进行数字化抽样,将波形数值保存在txt文档中去
- step 4:testbench文件的编写
- step 5:仿真结果
- step 6:Matlab仿真验证
- (3)FIR的FPGA实现与matlab仿真(FIR&汉明窗&100MHz采样&带通滤波):
- (4)滤波器FPGA实现方式原理示意:
- (5)文件汇总:
Written by @hzj
//JinXing Project
#2021.10.15 V1.0
#2021.10.19 V1.1
#2021.10.20 V1.2
Matlab仿真低通的FIR滤波器BLACKMAN窗并使用FPGA实现
(1)FIR&IIR介绍
- 巴特沃斯滤波器:最先由英国工程师斯蒂芬·巴特沃斯(Stephen Butterworth)在1930年提出,主要的特点是在阻带和通带上面都比较平坦,但是容易出现过渡带上失真的问题。有关常用的滤波器比较如下表所示。
| 滤波器名称 | 滤波器主要特点 |
|---|---|
| 巴特沃斯滤波器(Butterworth filter) | 阻带和通带上面都比较平坦,但是容易出现过渡带上失真,阻带的下降过程较慢,当滤波器的阶数越高,滤波器就越接近理想滤波器 |
| 椭圆滤波器(Elliptic Filter) | 在相同阶数时,椭圆滤波器阻带下降在几种滤波器中下降最快,过渡带更为陡峭、更窄 |
| 切比雪夫滤波器(Chebyshev Filter) | 通带阻带上幅频响应有等波纹波动。虽然能够拥有比巴特沃斯滤波器衰减更快的过渡带,但是幅频响应的平坦度没有巴特沃斯滤波器平坦。有根据幅频响应中通带和阻带有无等波纹情况分为Ⅰ型切比雪夫滤波器(通带有等波纹)和Ⅱ型切比雪夫滤波器(阻带有等波纹) |
| 贝塞尔滤波器(Bessel filter) | 具有最大平坦的群延迟(线性相位响应)的线性过滤器 |
| Compare: |
相同阶数下通频带下降陡峭度比较:**椭圆滤波器>切比雪夫滤波器>巴特沃斯滤波器>贝塞尔滤波器**
- 巴特沃斯滤波器的matlab实现的主要函数:
-
filter函数:y = filter(b,a,X) -b为分子系数向量,a为分母系数向量,向量X为代滤波的数据。 -
butter函数是算出巴特沃斯滤波器的系数,使用求得的系数,使用filter滤波函数对信号进行滤波。下面实现一个带通滤波器:通带频率大小为100Hz-200Hz,滤波器的阶数设置为8阶,采样频率设置为1000Hzbutter函数:[b,a] = butter(N,Wn,'high' / 'low' / ") -用来设计高通/低通/带通滤波器,N代表滤波器阶数
[b,a] = butter(8,[100/(1000/2) 200/(1000/2)])
//[b,a]=butter(n,[Wp/Fa Ws/Fa])
//Fa = Fs/2,Fs为采样频率
y = filter(b,a,x)
//使用巴特沃斯滤波器生成函数的b,a系数,滤除原始信号x的杂质,得到滤波完成后的波形信号y
上述是采用的matlab函数的实现方法,但是由于需要自己计算参数,没有图形界面直观,因此常常采用的是FDA设计插件进行设计,通过filterDesigner指令在matlab中唤出,通过COE文件导出量化系数进行卷积计算。
- 滤波器的线性相位,全通滤波器,群延迟之间的关系&滤波器设计:
链接1: 一文读懂滤波器的线性相位,全通滤波器,群延迟.
链接2: 数字滤波器设计(IIR与FIR).
(2)FIR的FPGA实现与matlab仿真(FIR&BLACKMAN窗&4MHz采样&低通滤波):
①采用Matlab中的FDA插件设计滤波器
matlab上使用filterDesigner参数,唤出matlab上的插件,设置响应类型为低通,设置FIR为窗函数(Blackman),采样频率设置为4MHz,截至频率为1MHz,打开缩放通带,设定FIR滤波器阶数为7阶。如下图所示。
所得到的FIR滤波器是稳定性滤波器,所有频率下的延迟都是相同的,因此,当波形经过滤波器后,各个频率合成的波形的形状不会发生变化,只是发生了迟延。这个性质对音乐的播放很有帮助,若是使用不同频率下的延迟不相同的滤波器(IIR),那么音乐中不同频率的到达人耳的时间不一样,一定会导致音乐品质发生变化。
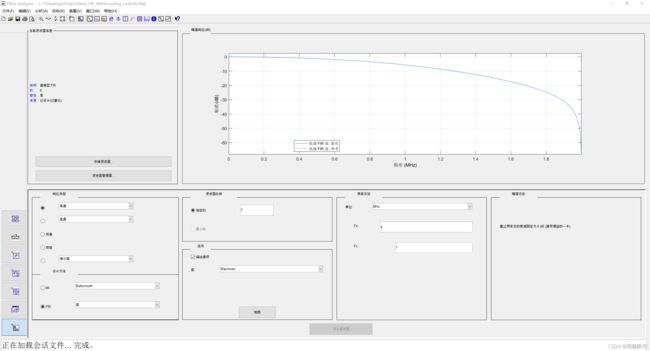
上图设置的是低通、FIR(BLACKMAN窗)、采样频率Fs为4MHz、截止频率Fc为1MHz。同时设置量化参数,如下图所示。

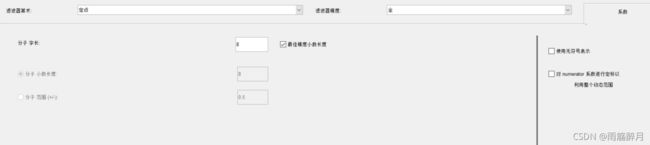
选择滤波器算术为定点,分子字长为8(这个地方的8相当于量化出来的滤波器量化系数值为8位,量化位数越高量化的就越精确,但是同时采用FPGA实现的时候就会消耗更多的硬件资源进行实现,因此我们择中考虑为8位,输出的位为xxxx_xxxx)
②FDA导出滤波器系数
在设计滤波器完成之后,需要将滤波器的参数进行导出。这里有两种导出方式,一是采用的Num系数直接导出法,最后自己进行量化;第二种是采用COE文件导出法,将导出的文件中的量化系数导出。下面分别简述导出方式。
- 采用Num系数矩阵导出法:
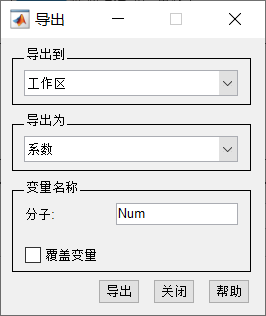
这个地方是将系数导出到Num数组中去,前提看下Num数组是否存在数据,有数据的话需要将数据删除再进行导出,否则可能会出现错误。

使用Num命令唤出当前数组array中的数据,并且进行量化。当然这个地方采用的是我自己设定的量化系数,可能和直接导出的量化系数不一样。 - 采用COE文件导出法:

保存coe文件后,然后在这个matlab上会自动出现以下的代码,里面coefdata中的数据就是量化系数(量化系数个数=滤波器阶数数+1)因此,这个地方应该就是有8位量化系数。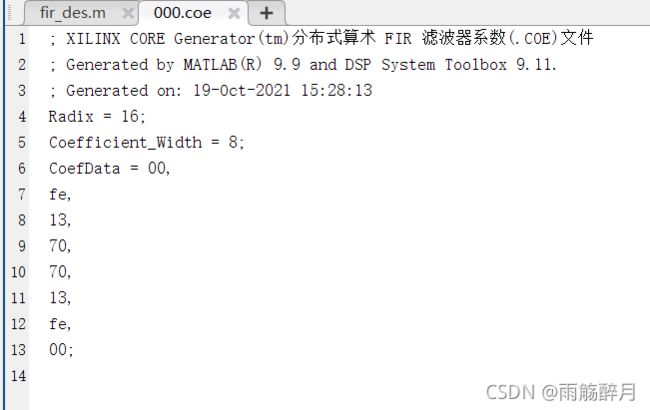
文本代码格式如下:
; XILINX CORE Generator(tm)分布式算术 FIR 滤波器系数(.COE)文件
; Generated by MATLAB(R) 9.9 and DSP System Toolbox 9.11.
; Generated on: 19-Oct-2021 15:28:13
Radix = 16;
Coefficient_Width = 8;
CoefData = 00,
fe,
13,
70,
70,
13,
fe,
00;
因此,采用这种方法得到的量化系数CoefData 为 00,fe,13,70,70,13,fe,00。可以发现具有对称性,我们后续的FPGA实现也采用这个量化系数来做。
③根据滤波器的量化系数使用FPGA代码实现
在得到滤波器的量化系数后,需要进行FPGA代码的实现。在本代码中,借鉴的是 matlab与FPGA数字滤波器设计(5)—— Verilog 串行 FIR 滤波器这篇文章的代码,自己并对代码进行了部分修改和优化,加上了部分注释。
step 1:建立好相关的工程文件(FIR_low8.v以及对应的tb文件)
step 2:Verilog代码书写
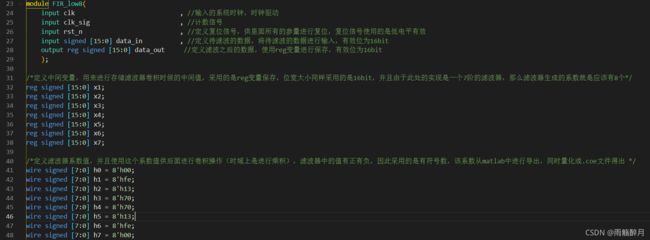
定义一个时钟信号clk与一个信号时钟信号clk_sig,保证时钟信号的频率是信号时钟信号clk_sig的8倍(这个地方的含义是每8个clk系统时钟时间,进行一次移位。然后在接下来的8个系统时钟clk中,由于有8个量化系数,因此要分别进行8次量化系数与输入波形数值的乘法);data_in代表16位待滤波信号数据的输入,data_out代表16位滤波后信号数据的输出;定义x1-x7共8个reg寄存器用来缓存当前进行滤波的8位数据;量化系数h1~h7共8个,采用COE文件中导出的值00,fe,13,70,70,13,fe,00。
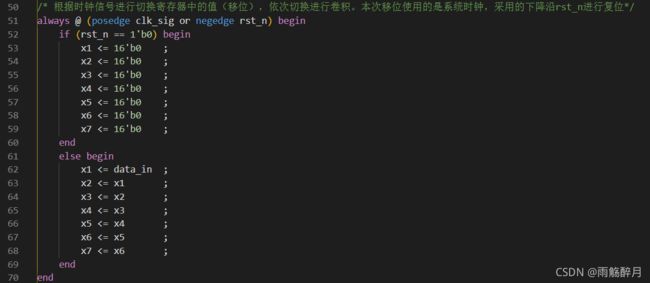
遇到信号时钟clk_sig上升沿或者是复位信号归零。遇复位信号时,将当前的待滤波信号缓冲区x1-x7中的值进行清零;当遇信号时钟clk_sig上升沿时,将新的一位的待滤波信号进行输入,进行下一轮卷积。
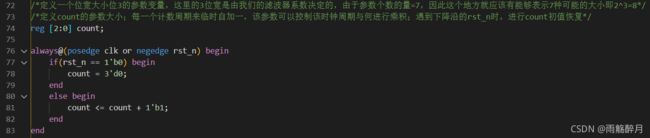
count用记录每一次卷积中乘积做到哪一个位次,8个量化系数需要进行8次乘积,依次从3’b000,3’b001,3’b010,3’b011,3’b100,3’b101,3’b110,3’b111共8种依次变化。当数值加满成3’b111,下一个clk来临时自动进位成3’b000,开始重新进行8次乘积以及乘积的累加。
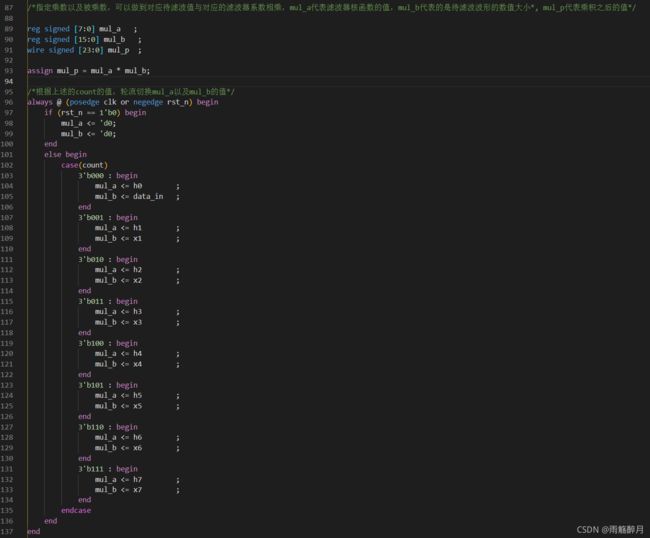
通过定义mul_a、mul_b、mul_p,并分别在每个时钟clk来临的时候进行mul_a、mul_b值的切换,从而依次乘积得到新的mul_p。这里还需要尤为注意一点,assign mul_p = mul_a * mul_b,两个有符号数(一个8位乘以一个16位的二进制数)最终的乘积结果位24位的有符号二进制数,因此定义mul_p应该是wire signed [23:0] mul_p这样的方式,都是采用补码的方式进行展示。
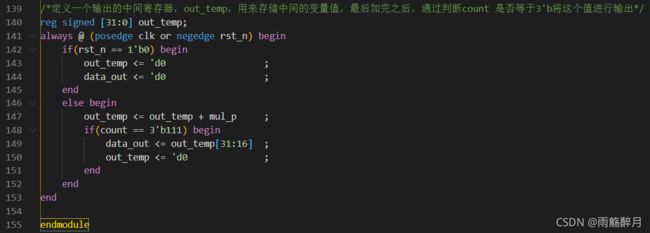
最后一个always语句是控制out_temp这个缓存区中的累加和,每8个clk时钟(或者称之为每1个clk_sig时钟),进行缓存区的赋值(data_out <= out_temp[31:16])和缓存区的清零(out_temp <= 'd0 )。同时由于规定输出的滤波数据应该是16位的,所以使用data_out <= out_temp[31:16] 这个语句,只采用高16位的值,忽略低16位的值,相当于做一个除法,除以2^16,将权值较大的保留,较小的去除,做一个滤波后输出波形的等比例缩小。
step 3:生成待滤波波形,并且使用matlab对波形进行数字化抽样,将波形数值保存在txt文档中去
matlab波形生成代码如下:
// A code block
var foo = 'bar';%设置源波形以及杂波波形的频率,这里选择的采样频率位4MHz
f1 = 0.4;
f2 = 1.97;
Fs = 4;
N = 16;%设置量化位数,控制后面数字化输出波形的中的数据值,量化位数越高,波形数据还原
%就越准确,但是同时后面就会消耗更多的FPGA硬件资源,因此综合考虑,我们data_in采用的
%16位输入,这里量化也采用的是16位
t = 0:1/Fs:20;
c1 = 2*pi*f1*t;
c2 = 2*pi*f2*t;
%波形合成,源波采用1倍幅值,杂波采用0.5倍幅值,使用s1+s2进行波形合成
s1 = sin(c1);
s2 = 0.5*sin(c2);
s = s1+s2;
%归一化
s = s/max(abs(s));
%等比例放大波形的数值,方便进行二进制化
Q_s = round(s*(2^(N-1) - 1));
fid = fopen('C:路径\sin_ten.txt','w');%十进制变换,保存十进制数到路径
fprintf(fid, '%16d\r\n',Q_s);
fprintf(fid, ';');
fclose(fid);
fid = fopen('C:路径\sin.txt','w');
for k=1:length(Q_s)%二进制变换,保存二进制数到路径
B_s=dec2bin(Q_s(k)+((Q_s(k))<0)*2^N,N);
for j=1:N
if B_s(j)=='1'
tb=1;
else
tb=0;
end
fprintf(fid,'%d',tb);
end
fprintf(fid,'\r\n');
end
fprintf(fid,';');
fclose(fid);
step 4:testbench文件的编写
已经生成了待滤波的数据文件,保存在sin.txt中。现在我们需要使用已经写好的verilog代码对数据进行滤波输出,因此需要书写.tb文件。同样的采用前几讲中的testbench&vscode模板书写。
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2021/10/16 14:50:22
// Design Name:
// Module Name: tb
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
`timescale 1ns / 1ps
module tb_FIR_low8;
// FIR_low8 Parameters
parameter PERIOD = 10;
// FIR_low8 Inputs
reg clk ;
reg clk_sig ;
reg rst_n ;
reg [15:0] data_in ;
// FIR_low8 Outputs
wire [15:0] data_out ;
integer i;
initial
begin
clk = 0 ;
clk_sig = 0 ;
rst_n = 0 ;
data_in = 0 ;
i = 1 ; //此处是从1开始计数,也就是说data_men中的第一个数的下标为[1],而非[0]
end
initial
begin
forever #(PERIOD/2) clk =~clk; //clk的周期
end
initial
begin
forever #(PERIOD*4) clk_sig = ~clk_sig; //clk_sig的周期为clk的8倍
end
initial
begin
#(PERIOD*2) rst_n = 1; //复位信号
end
parameter data_num = 32'd10000;
reg [15:0] data_men[data_num:1];
initial begin
$readmemb("C:路径/sin.txt",data_men); //注意斜杠的方向,不能反<<<<<<<
end
always @(posedge clk_sig) begin //每1个clk_sig信号来临后,进行一次数据输入,将新的一个波形数据输入data_in中。
data_in <= data_men[i];
i <= i+1;
end
FIR_low8 u_FIR_low8 (
.clk ( clk ),
.clk_sig ( clk_sig ),
.rst_n ( rst_n ),
.data_in ( data_in [15:0] ),
.data_out ( data_out [15:0] )
);
endmodule
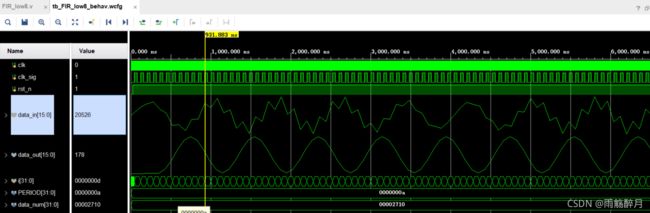
step 5:仿真结果
step 6:Matlab仿真验证
为了验证滤波器的滤波结果,使用原来的量化系数进行matlab滤波仿真,以验证我们的FPGA设计实现的滤波效果有没有达到。验证仿真使用的matlab代码如simulation.m所示,代码如下:
Fs = 4; %4M的采样频率sample
t = 0:1/Fs:20-1/Fs; %设置精确的采样点
N = 20 * Fs; %设置采样点数, 总共的采样点数为80
f1 = 0.4; %源波频率0.4MHz
f2 = 1.97; %杂波频率1.97MHz
c1 = 2*pi*f1*t;
c2 = 2*pi*f2*t;
s1 = sin(c1);
s2 = 0.5*sin(c2);
s = s1+s2; %波形合成
x_in= s;
%输入信号
figure(1);
subplot(1,2,1)
plot(t,x_in);
title('输入信号');
xlabel('时间');
ylabel('幅度');
subplot(1,2,2);
SpectrumX= fft(x_in,N);
M=0:1:N-1;
stem(M,abs(SpectrumX));
title('输入信号FFT');
%滤波
y=zeros(1,N);
lastr0=0;
lastr1=0;
lastr2=0;
lastr3=0;
lastr4=0;
lastr5=0;
lastr6=0;
lastr7=0;
for i=1:1:N
newr0 = x_in(i)*0;
newr1 = lastr0 + x_in(i) * -2;
newr2 = lastr1 + x_in(i) * 13;
newr3 = lastr2 + x_in(i) * 70;
newr4 = lastr3 + x_in(i) * 70;
newr5 = lastr4 + x_in(i) * 13;
newr6 = lastr5 + x_in(i) * -2;
newr7 = lastr6 + x_in(i) * 0;
lastr0 = newr0 ;
lastr1 = newr1 ;
lastr2 = newr2 ;
lastr3 = newr3 ;
lastr4 = newr4 ;
lastr5 = newr5 ;
lastr6 = newr6 ;
y(i)=newr7;
end
%输出信号
figure(2);
subplot(1,2,1);
plot(t,y);
len_of_y=length(y);
SpectrumY= fft(y ,len_of_y);
title('输出信号');
xlabel('时间');
ylabel('幅度');
subplot(1,2,2);
N=0:1:len_of_y-1;
stem(N,abs(SpectrumY));
title('输出信号FFT');
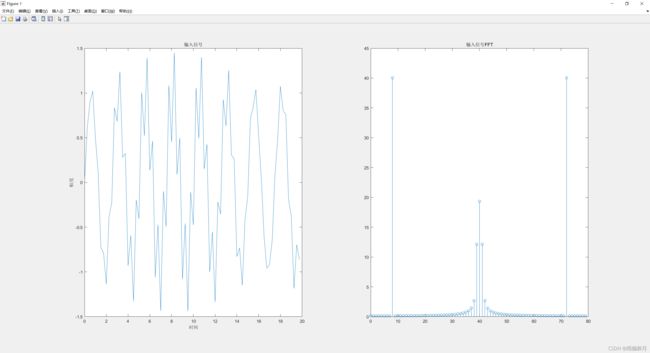
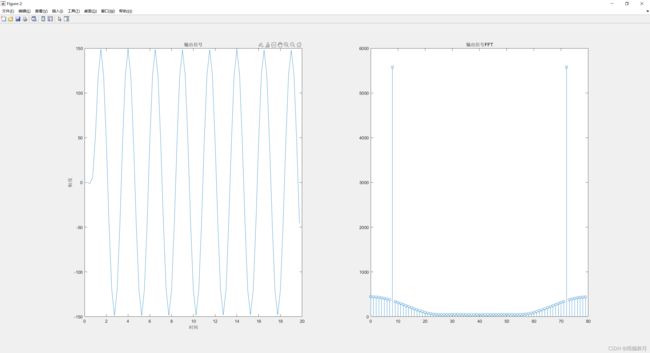
使用代码仿真验证的波形如下图所示,分别是输入信号、输入信号的FFT以及输出信号、输出信号的FFT。
输入信号与输入信号的FFT:
(3)FIR的FPGA实现与matlab仿真(FIR&汉明窗&100MHz采样&带通滤波):
- 带通滤波&FIR实现与前文中的低通滤波器的实现较为相似,流程也基本上是一样的。因此,相关详情不再进行赘述。直接操作。
- FDA文件的设计,阶数设置为19阶,对应会生成20个量化系数,采用汉明窗的方法。采样频率Fs设置大小为100MHz,带通通带频率范围为20MHz-30MHz。量化的分子字长同样采用的8位字长。
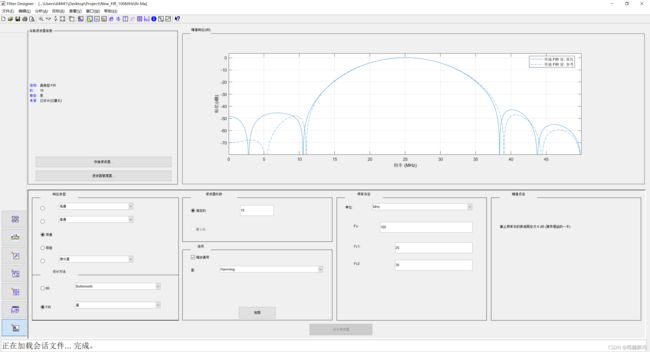
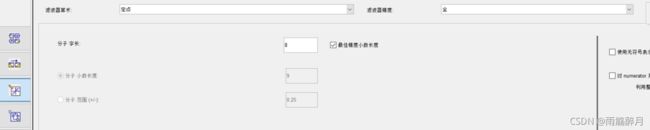
- 导出COE文件中的量化系数CoefData = 00, 02, 05, f5, ea, 24, 34, bc, b0, 57, 57, b0, bc, 34, 24, ea, f5, 05, 02, 00。
- 采样导出的量化系数进行设计,对应的Verilog代码实现如下所示:
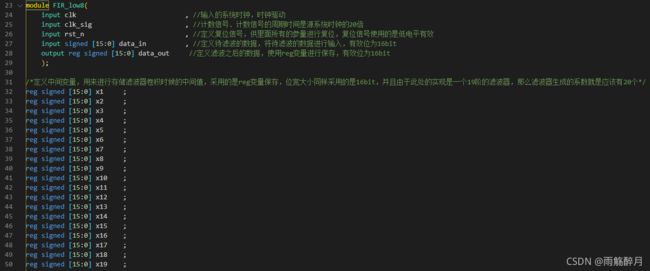
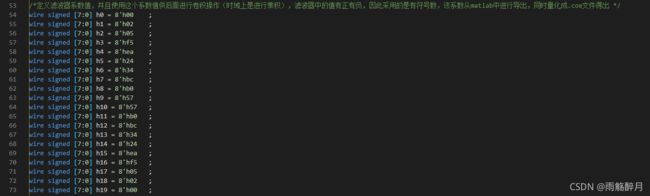
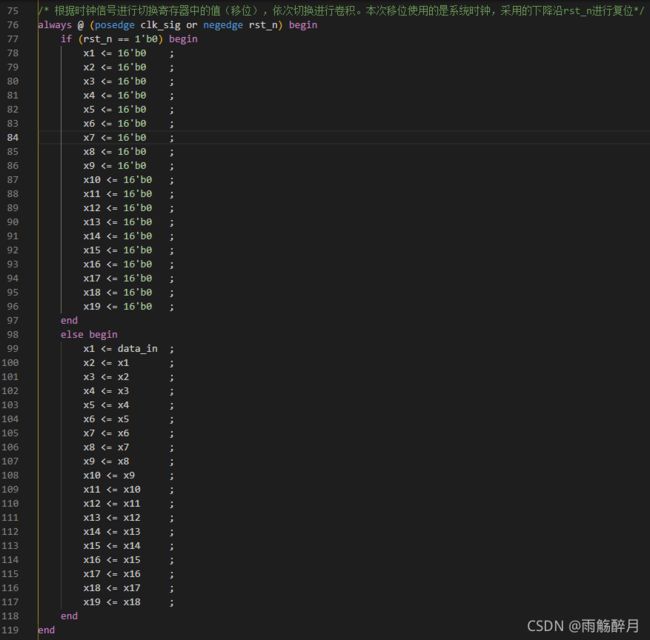
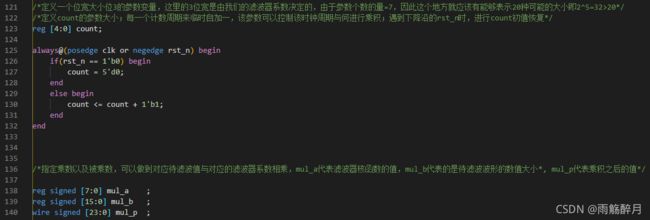
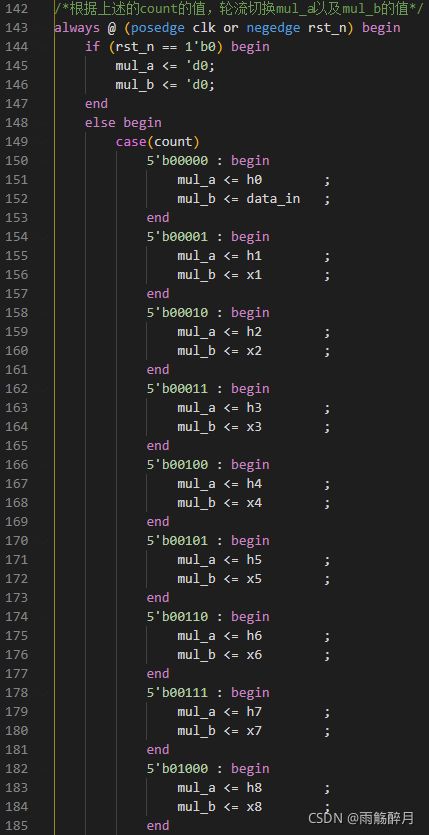
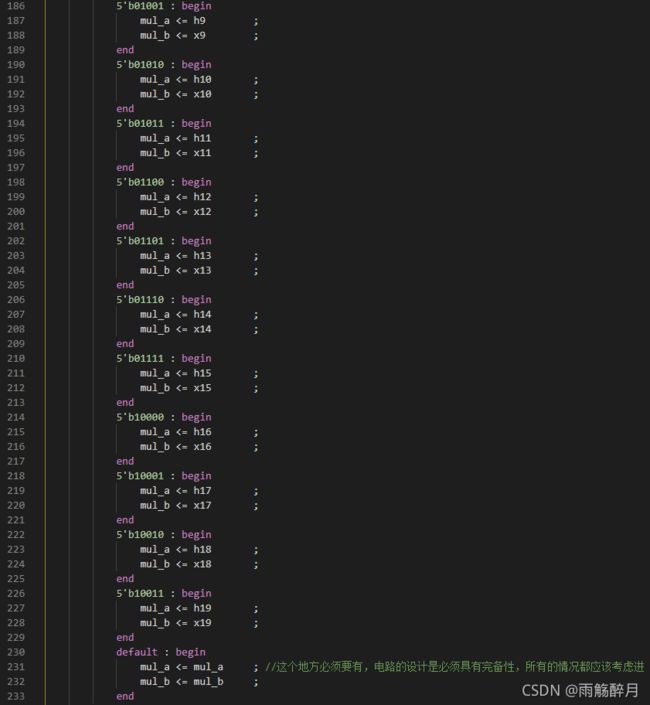
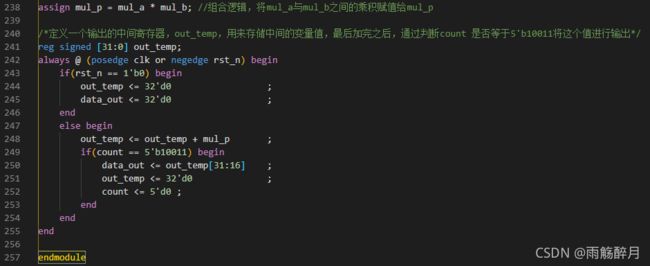
- tb测试文件实现如下所示:
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2021/10/16 14:50:22
// Design Name:
// Module Name: tb
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
`timescale 1ns / 1ps
module tb_FIR_low8;
// FIR_low8 Parameters
parameter PERIOD = 10;
// FIR_low8 Inputs
reg clk ;
reg clk_sig ;
reg rst_n ;
reg [15:0] data_in ;
// FIR_low8 Outputs
wire [15:0] data_out ;
integer i;
initial
begin
clk = 0 ;
clk_sig = 0 ;
rst_n = 0 ;
data_in = 0 ;
i = 1 ; //此处是从1开始计数,也就是说data_men中的第一个数的下标为[1],而非[0]
end
initial
begin
forever #(PERIOD/2) clk =~clk; //clk的周期
end
initial
begin
forever #(PERIOD*10) clk_sig = ~clk_sig; //clk_sig的周期为clk的8倍
end
initial
begin
#(PERIOD*2) rst_n = 1; //复位信号
end
parameter data_num = 32'd10000;
reg [15:0] data_men[data_num:1];
initial begin
$readmemb("C:路径/sin.txt",data_men); //注意斜杠的方向,不能反<<<<<<<
end
always @(posedge clk_sig) begin //每1个clk_sig信号来临后,进行一次数据输入,将新的一个波形数据输入data_in中。
data_in <= data_men[i];
i <= i+1;
end
FIR_low8 u_FIR_low8 (
.clk ( clk ),
.clk_sig ( clk_sig ),
.rst_n ( rst_n ),
.data_in ( data_in [15:0] ),
.data_out ( data_out [15:0] )
);
endmodule
- 生成复合信号(低频+中频),并转化为2进制进行存储。 这里采用的源信号是25MHz,两个杂波信号为5.5MHz与10.5MHz。波形的采样频率与FDA设计时选用的Fs=100MHz一致。输出的波形数据位数为16位。
f1 = 25;
f2 = 5.5;
f3 = 10.5;
Fs = 100;
N = 16;
end_num = 5;
t = 0:1/Fs:end_num-1/Fs;
c1 = 2*pi*f1*t;
c2 = 2*pi*f2*t;
c3 = 2*pi*f3*t;
s1 = sin(c1);
s2 = 0.5*sin(c2);
s3 = 0.2*sin(c3)
s = s1+s2+s3;
s = s/max(abs(s));
Q_s = round(s*(2^(N-1) - 1));
fid = fopen('C:路径\sin_ten.txt','w');
fprintf(fid, '%16d\r\n',Q_s);
fprintf(fid, ';');
fclose(fid);
fid = fopen('C:路径\sin.txt','w');
for k=1:length(Q_s)%二进制变换
B_s=dec2bin(Q_s(k)+((Q_s(k))<0)*2^N,N);
for j=1:N
if B_s(j)=='1'
tb=1;
else
tb=0;
end
fprintf(fid,'%d',tb);
end
fprintf(fid,'\r\n');
end
fprintf(fid,';');
fclose(fid);
- 将实现的代码进行仿真,波形仿真效果如下。可以看到,低频信号已经被滤除,保留下了中频信号25MHz。
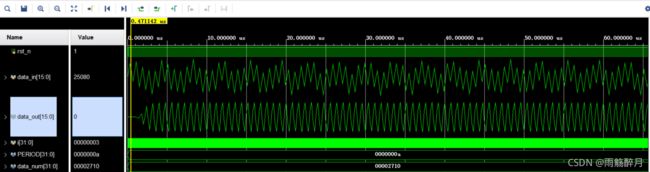
- 最后同样的,为了验证我们的带通滤波器的实现是正确的,同样需要构造一个Matlab仿真程序,查看经过设计的带通滤波器之后的波形效果图。同样将代码贴下:
Fs = 100; %100M的采样频率sample
end_num = 5;
t = 0:1/Fs:end_num-1/Fs; %设置精确的采样点
N = end_num * Fs; %设置采样点数, 总共的采样点数为20 * Fs;
f1 = 25; %源波频率25MHz
f2 = 5.5; %杂波频率5.5MHz
f3 = 10.5; %杂波频率10.5MHz
c1 = 2*pi*f1*t;
c2 = 2*pi*f2*t;
c3 = 2*pi*f3*t;
s1 = sin(c1);
s2 = 0.5*sin(c2);
s3 = 0.2*sin(c3)
s = s1+s2+s3; %波形合成
x_in= s;
%输入信号
figure(1);
subplot(1,2,1)
plot(t,x_in);
title('输入信号');
xlabel('时间');
ylabel('幅度');
subplot(1,2,2);
SpectrumX= fft(x_in,N);
M=0:1:N-1;
stem(M,abs(SpectrumX));
title('输入信号FFT');
%滤波
y=zeros(1,N);
lastr0=0;
lastr1=0;
lastr2=0;
lastr3=0;
lastr4=0;
lastr5=0;
lastr6=0;
lastr7=0;
lastr8=0;
lastr9=0;
lastr10=0;
lastr11=0;
lastr12=0;
lastr13=0;
lastr14=0;
lastr15=0;
lastr16=0;
lastr17=0;
lastr18=0;
for i=1:1:N
newr0 = x_in(i) * 00;
newr1 = lastr0 + x_in(i) * 02;
newr2 = lastr1 + x_in(i) * 05;
newr3 = lastr2 + x_in(i) * -11;
newr4 = lastr3 + x_in(i) * -22;
newr5 = lastr4 + x_in(i) * 36;
newr6 = lastr5 + x_in(i) * 52;
newr7 = lastr6 + x_in(i) * -68;
newr8 = lastr7 + x_in(i) * -80;
newr9 = lastr8 + x_in(i) * 87;
newr10 = lastr9 + x_in(i) * 87;
newr11 = lastr10 + x_in(i) * -80;
newr12 = lastr11 + x_in(i) * -68;
newr13 = lastr12 + x_in(i) * 52;
newr14 = lastr13 + x_in(i) * 36;
newr15 = lastr14 + x_in(i) * -22;
newr16 = lastr15 + x_in(i) * -11;
newr17 = lastr16 + x_in(i) * 05;
newr18 = lastr17 + x_in(i) * 02;
newr19 = lastr18 + x_in(i) * 00;
lastr0 = newr0 ;
lastr1 = newr1 ;
lastr2 = newr2 ;
lastr3 = newr3 ;
lastr4 = newr4 ;
lastr5 = newr5 ;
lastr6 = newr6 ;
lastr7 = newr7 ;
lastr8 = newr8 ;
lastr9 = newr9 ;
lastr10 = newr10 ;
lastr11 = newr11 ;
lastr12 = newr12 ;
lastr13 = newr13 ;
lastr14 = newr14 ;
lastr15 = newr15 ;
lastr16 = newr16 ;
lastr17 = newr17 ;
lastr18 = newr18 ;
y(i)=newr19;
end
%输出信号
figure(2);
subplot(1,2,1);
plot(t,y);
len_of_y=length(y);
SpectrumY= fft(y ,len_of_y);
title('输出信号');
xlabel('时间');
ylabel('幅度');
subplot(1,2,2);
N=0:1:len_of_y-1;
stem(N,abs(SpectrumY));
title('输出信号FFT');
对应的输入信号的波形以及FFT变化如下:
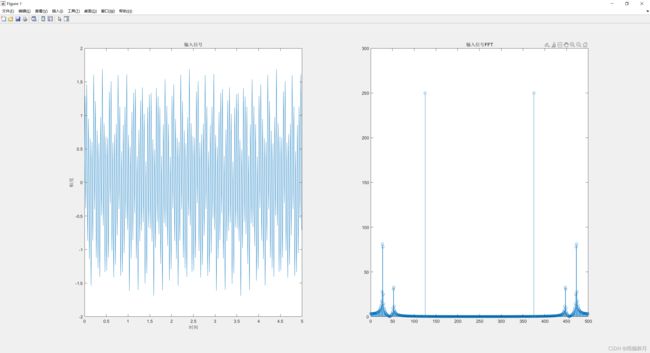
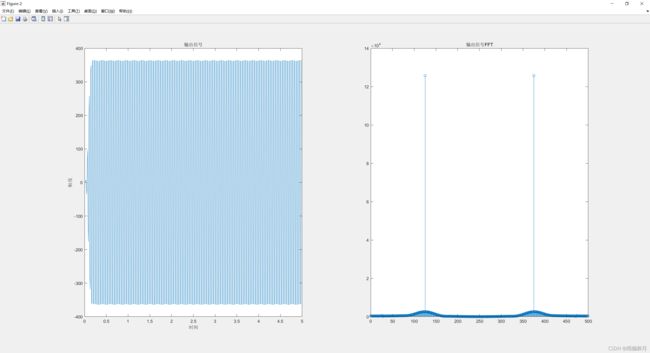
通过上述的仿真结果,可以看出两个低频分量已经被滤除了,和上面Vivado的仿真结构一样。可以证明此带通滤波器已经实现了。
(4)滤波器FPGA实现方式原理示意:
clk_sig信号控制着输入数据的读入,数据一个一个被读进寄存器中,然后再8个clk的时钟周期上一次进行乘积,并累加。最终完成一个数据输入后的一次完整卷积操作,主要的示意图如下所示。
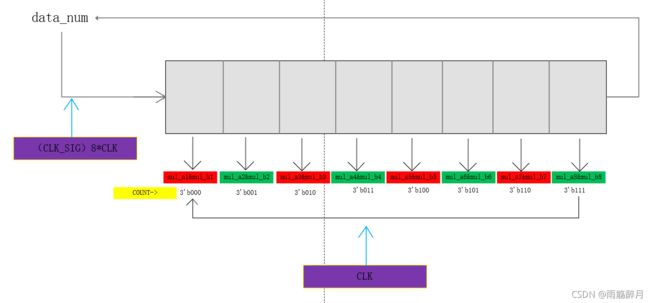
(5)文件汇总:
-
FIR的FPGA实现与matlab仿真(FIR&BLACKMAN窗&4MHz采样&低通滤波)
-
FIR的FPGA实现与matlab仿真 (FIR&汉明窗&100MHz采样&带通滤波)
文档中所有已使用的代码已经放在中。fir.fda为filterDesigner设计代码,fir_des.m为待滤波形模拟生成文件,simulation.m为滤波器仿真测试文件。tb.v为FIR_low8.v文件的测试代码。


Verilog_FIR_4M是FIR&BLACKMAN窗&4MHz采样&低通滤波代码。
Verilog_FIR_100MHz是FIR&汉明窗&100MHz采样&带通滤波代码。
上述代码文件放在了 FIR的低通滤波器、带通滤波器Verilog代码实现与Matlab仿真测试链接中。