深度学习(九) GAN 生成对抗网络 理论部分
GAN 生成对抗网络 理论部分
- 前言
- 一、Pixel RNN
-
- 1.图片的生成模型
- 2.Pixel RNN
- 3.Pixel CNN
- 二、VAE(Variational Autoencoder)
-
- 1.VAE的优缺点
- 2.KL散度
- 3.隐变量与隐变量模型
- 4.VAE的用途
- 5.VAE的结构
- 6.VAE的实现
- 7.VAE的公式推导
- 三、GAN(生成对抗网络)
-
- 1.JS散度
- 2.Wasserstein距离
-
- 1.Wasserstein距离简介
- 2.为什么要使用Wassertain距离?
- 3.Wassertain距离的公式推导
- 3.GAN的优缺点
- 4.GAN的应用领域
- 5.GAN的基本组成
- 6.GAN的训练过程
- 7.GAN的优化
- 8.WGAN
- 9.Mode Collapse(模式塌陷)
- 10.Mode Dropping
- 四、其他的GAN网络
-
- 1.Conditional GAN(条件生成对抗网络)
- 2.Cycle GAN(循环生成对抗网络)
- 3.Energy-based GAN (EBGAN)
- 总结
前言
接下来将会介绍另外一种网络:生成对抗网络,这种网络在最近十分的流行,不同于之前所学的CNN,RNN,GAN有其独特的旗帜。
一、Pixel RNN
1.图片的生成模型
生成模型通过学习样本点的分布,得到联合概率P(X,Y),图像是具有概率分布。我们对图像中原始像素点的离散概率建模,并编码图像整个集的依赖性,从而通过概率分布去预测图片。
无论是Pixel RNN还是Pixel CNN,我们都假设一个像素的值仅取决于它之前的像素的值,即:
p ( x n ) = p ( x n ∣ x n − 1 ) p ( x n − 1 ∣ x n − 2 ) p ( x n − 2 ∣ x n − 3 ) . . . p ( x 2 ∣ x 1 ) p(x_n)=p(x_n|x_{n-1})p(x_{n-1}|x_{n-2})p(x_{n-2}|x_{n-3})...p(x_{2}|x_{1}) p(xn)=p(xn∣xn−1)p(xn−1∣xn−2)p(xn−2∣xn−3)...p(x2∣x1)
2.Pixel RNN
传统的Pixel RNN是利用我们前面讲过的LSTM对图片进行处理的。LSTM中一次读取图像的一行,并使用一维卷积层对其进行处理,然后将激活信息馈送到后续层中以预测该行的像素。

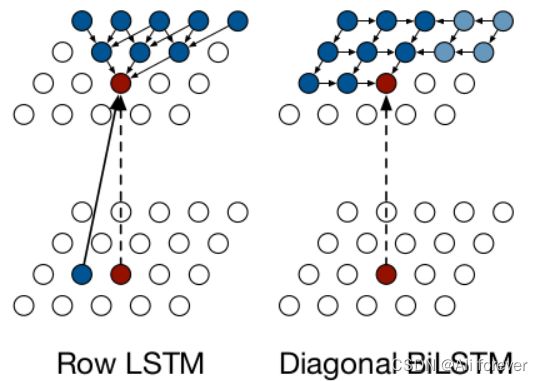
可以看到通过映射后,Row LSTM的感知域是一个三角形区域,并且卷积中要利用先前的状态 h t − 1 h_{t-1} ht−1跟本状态一起卷积得到下一层。
而Diagnoal BiLSTM由于是双向的LSTM,并行计算和捕获任何图像大小的整个可用上下文。每个层的两个方向都以对角线方式扫描图像,从顶部的一个角开始,并到达底部的相反角。计算中的每个步骤一次计算图像中沿对角线的 LSTM 状态,就会得到如图的感知域。
3.Pixel CNN
Pixel RNN由于感受野内具有潜在的无边界的依赖范围,会浪费很多的计算成本,但如果我们将感知域扩大后,就可以减少这种情况。
Pixel CNN 使用多个卷积层来保留空间分辨率,不使用池化层。掩码在卷积中采用,以避免看到未来内容。
Pixel CNN中利用 mask 机制,将未来的 context 遮蔽,就实现了随着时间演进的序列模型。
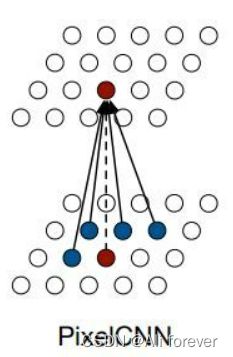 与 PixelRNN 相比,PixelCNN 的并行功能的优势仅在训练或评估测试图像时可用。图像生成过程对于两种网络都是连续的,因为每个采样的像素需要作为输入返回到网络。
与 PixelRNN 相比,PixelCNN 的并行功能的优势仅在训练或评估测试图像时可用。图像生成过程对于两种网络都是连续的,因为每个采样的像素需要作为输入返回到网络。
二、VAE(Variational Autoencoder)
1.VAE的优缺点
- 优点
- VAE就生成式模型来说是一种有据可循的方法,它使得查询推断称为可能,如此一来便能够推断出像 这样的分布,这些东西对其他任务来说会是很有用的特征表征。也就是说破除了一定的黑盒性。
- VAE给隐向量添加了噪声,使得隐向量的编码区域由离散变为连续,扩大了编码区域,减少了隐向量空间的失真点。
- VAE不仅拥有自编码器的作用(降维),还可以用于数据的生成。
- 缺点
- VAE从来都没有去学习如何产生一张新的图片,只是保证产生一张与数据库中的图片尽可能相似的而已,VAE做的只是模仿,没有办法产生新的图片。
- VAE没有使用对抗网络,生成的图片一般都比较模糊
2.KL散度
KL散度用来衡量两个分布之间的差异,度量两个概率分布函数之间的“距离”。
K L [ P ( x ) ∣ ∣ Q ( x ) ] = ∑ x ∈ X P ( x ) log P ( x ) Q ( x ) = E x ∈ P ( x ) log P ( x ) Q ( x ) KL[P(x)||Q(x)]=\sum_{x\in X}P(x)\log{\frac{P(x)}{Q(x)}}=E_{x\in P(x)}\log{\frac{P(x)}{Q(x)}} KL[P(x)∣∣Q(x)]=x∈X∑P(x)logQ(x)P(x)=Ex∈P(x)logQ(x)P(x)
可以看到KL散度与x是没有关系的,只与他们的概率分布有关。
对数函数是凸函数,所以KL散度的值为非负数,并且可以采用梯度下降去进行优化
很显然,KL散度越小,说明概率 Q 与概率 P 之间越接近,那么估计的概率分布与真实的概率分布也就越接近,所以我们需要尽可能令KL散度为零。
事实上,KL散度并不能表征真正的距离,因为他们不满足互换性,也不满足三角距离不等式。
3.隐变量与隐变量模型
- 隐变量:不可直接观测的综合性变量。
- 隐变量模型: 隐变量模型是一种概率模型,其中某些变量是不可观测的。
隐变量可以通过数学模型推导出来,但是十分的困难,有些情况下,潜变量和现实中的一些因素是有关系的,而有些情况下指的是抽象概念,例如分类、行为、心理状态、数据结构等等。
使用潜变量的好处之一是潜变量能用来降低数据的维度。大量的观测变量能够被整合起来成为一个潜变量来表示深层次的概念,使得观测数据更容易理解。
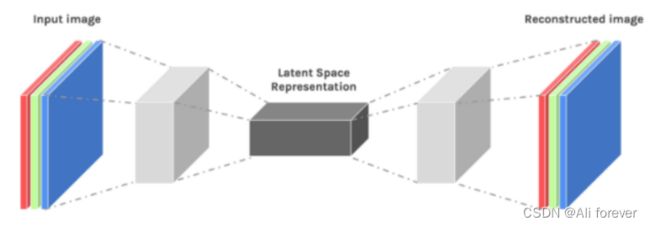
我们可以看到隐变量的维数明显要比其他情况低,事实上模型需要重建压缩数据(见解码器),它必须学会存储所有相关信息,忽略噪声。这就是压缩的价值所在——它可以让我们去掉任何无关的信息,只关注最重要的特性。训练到最后时,每个图像只有最重要的特征被存储在潜在空间表示中。
4.VAE的用途
VAE 模型是一种包含隐变量的生成模型,它利用神经网络训练得到两个函数(也称为推断网络和生成网络),进而生成输入数据中不包含的数据。
VAE 模型在生成多种复杂数据方面已经显示出了巨大的潜力,包括手写数字图像、人脸图像、门牌号图像、CIFAR 图像、场景物理模型、分割图像以及从静态图像进行预测等。
5.VAE的结构
VAE其实本质上亦是一种auto-encoder(自编码器),自编码器是一类在半监督学习和非监督学习中使用的人工神经网络,其功能是通过将输入信息作为学习目标,对输入信息进行表征学习。
AutoEncoder 包括 编码器(Encoder) 和 解码器(Decoder) 两部分。Encoder 过程是将原先的数据(常用于图像方向)压缩为低维向量;Decoder 则是把低维向量还原为原来数据。

VAE生成的不再是简单的特征,而是一个分布,包括均值 μ \mu μ,方差 σ \sigma σ,噪声 e e e,噪声 e e e是按照正太分布采样出来的。最后生成的特征为
c i = e x p ( σ i ) ∗ e i + m i c_i=exp(\sigma_i)*e_i+m_i ci=exp(σi)∗ei+mi 避免了自编码器只简单重构原来的特征,导致过拟合,产生不理想的模型泛化能力。加入的噪声,则给模型生成了更多的可能性。
然后在做完Loss Function后,我们还要保证这个式子的最小化:
∑ i = 1 3 ( e x p ( σ i ) − ( 1 + σ i ) + ( m i ) 2 ) \sum_{i=1}^3(exp(\sigma_i)-(1+\sigma_i)+(m_i)^2) i=1∑3(exp(σi)−(1+σi)+(mi)2)
前面半截是为了保证 σ i \sigma_i σi的取值一定在零附近,满足高斯分布,因为只有在0附近时 e x p ( σ i ) − ( 1 + σ i ) exp(\sigma_i)-(1+\sigma_i) exp(σi)−(1+σi)才会很靠近零,而 m i m_i mi则用于正则化,保证其均值的稳定。
6.VAE的实现
VAE中,一般我们的样本先验概率 x x x分布是很难直接获取的,那么我们可以假设存在一个与 x x x对应的隐式表征 z z z的分布是一个先验分布,一般我们设置为高斯分布和其他比较简单的分布.
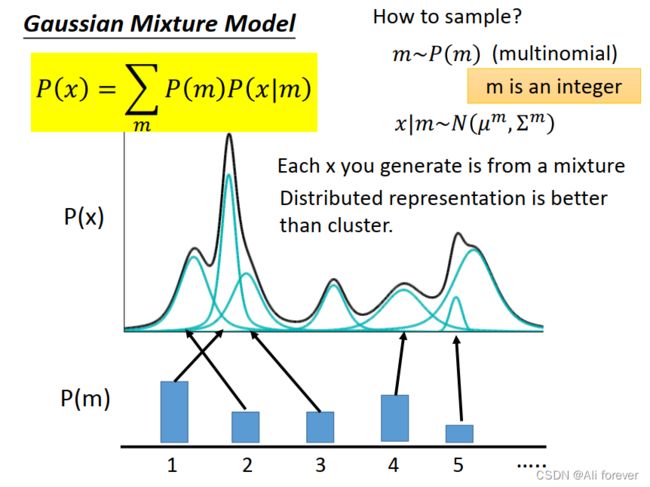
那么我们在样本生成阶段,我们可以通过标准正态分布采样得到 z ∼ p θ ∗ ( z ) z \sim p_{\theta^*(z)} z∼pθ∗(z),然后解码得到样本近似分布,再在此分布上采样来生成样本。其中 θ ∗ \theta^* θ∗是有关于先验假设和条件概率分布的参数,需要我们估计得出。
p θ ( x ) = ∫ p θ ( z ) p θ ( x ∣ z ) d z p_\theta(x)=\int p_\theta(z)p_\theta(x|z)dz pθ(x)=∫pθ(z)pθ(x∣z)dz
但是很明显,我们计算 p ( x ∣ z ) p(x|z) p(x∣z)的概率分布是非常难获取的,从而导致 p ( z ∣ x ) p(z|x) p(z∣x)也是十分困难的,所以我们利用 z z z这一个假设的隐变量去推出 x x x的概率分布也是很困难的。
为了解决这一个问题,我们就需要额外定义一个编码器 q ( z ∣ x ) q(z|x) q(z∣x),然后输入 x x x,通过 x x x的特征推导出某些 z z z,从而利用这个 q ( z ∣ x ) q(z|x) q(z∣x)去迫近我们的 p ( z ∣ x ) p(z|x) p(z∣x),然后通过解码器网络把 z z z映射到图像 x x x

7.VAE的公式推导
由上面内容可以知道我们的损失函数采用的是最大似然函数,这是VAE的核心内容,也是通过EM算法演变而来的,即:
L = ∑ x log P ( x ) L=\sum_x\log P(x) L=x∑logP(x)
log P ( x ) = ∫ z Q ( z ∣ x ) log P ( x ) d z = ∫ z Q ( z ∣ x ) log P ( x , z ) P ( z ∣ x ) d z = ∫ z Q ( z ∣ x ) log P ( x , z ) Q ( z ∣ x ) Q ( z ∣ x ) P ( z ∣ x ) d z = ∫ z Q ( z ∣ x ) log P ( x , z ) Q ( z ∣ x ) d z + ∫ z Q ( z ∣ x ) log Q ( z ∣ x ) P ( z ∣ x ) d z \begin{align} \log P(x) &=\int_z Q(z|x) \log P(x) dz \\ &=\int_z Q(z|x) \log \frac{P(x,z)}{P(z|x)} dz \\ &=\int_z Q(z|x) \log \frac{P(x,z)}{Q(z|x)}\frac{Q(z|x)}{P(z|x)} dz\\ &= \int_z Q(z|x) \log \frac{P(x,z)}{Q(z|x)}dz+\int_z Q(z|x) \log \frac{Q(z|x)}{P(z|x)} dz \end{align} logP(x)=∫zQ(z∣x)logP(x)dz=∫zQ(z∣x)logP(z∣x)P(x,z)dz=∫zQ(z∣x)logQ(z∣x)P(x,z)P(z∣x)Q(z∣x)dz=∫zQ(z∣x)logQ(z∣x)P(x,z)dz+∫zQ(z∣x)logP(z∣x)Q(z∣x)dz
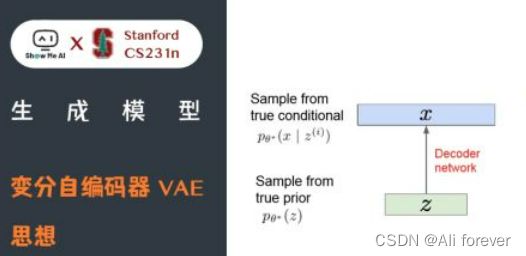
我们可以观察到后面那一项是我们的KL散度公式: K L ( Q ( z ∣ x ) ∣ ∣ P ( z ∣ x ) ) KL(Q(z|x)||P(z|x)) KL(Q(z∣x)∣∣P(z∣x))虽然它的值我们不确定,但是一定是大于等于0的数,我们将前面那一项定义为 L b L_b Lb,所以我们的原式可以为:
log P ( x ) ≥ ∫ z Q ( z ∣ x ) log P ( x , z ) Q ( z ∣ x ) d z \log P(x) \geq \int_z Q(z|x) \log \frac{P(x,z)}{Q(z|x)}dz logP(x)≥∫zQ(z∣x)logQ(z∣x)P(x,z)dz
下面我们队 L b L_b Lb继续进行化简:
L b = ∫ z Q ( z ∣ x ) log P ( x , z ) Q ( z ∣ x ) d z = ∫ z Q ( z ∣ x ) log P ( x ∣ z ) P ( z ) Q ( z ∣ x ) d z = ∫ z Q ( z ∣ x ) log P ( z ) Q ( z ∣ x ) d z + ∫ z Q ( z ∣ x ) log P ( z ∣ x ) d z = − K L ( Q ( z ∣ x ) ∣ ∣ P ( z ) ) + E z ∼ Q ( z ∣ x ) [ log P ( z ∣ x ) ] \begin{align} L_b&=\int_z Q(z|x) \log \frac{P(x,z)}{Q(z|x)}dz\\ &=\int_z Q(z|x) \log \frac{P(x|z)P(z)}{Q(z|x)}dz\\ &=\int_z Q(z|x) \log \frac{P(z)}{Q(z|x)}dz+\int_z Q(z|x) \log P(z|x)dz\\ &=-KL(Q(z|x)||P(z))+E_{z\sim Q(z|x)}[\log P(z|x)] \end{align} Lb=∫zQ(z∣x)logQ(z∣x)P(x,z)dz=∫zQ(z∣x)logQ(z∣x)P(x∣z)P(z)dz=∫zQ(z∣x)logQ(z∣x)P(z)dz+∫zQ(z∣x)logP(z∣x)dz=−KL(Q(z∣x)∣∣P(z))+Ez∼Q(z∣x)[logP(z∣x)]
从而得出结论:由于散度KL我们需要越接近零越好,所以我们的ELBO最理想情况下就是等于 E z ∼ Q ( z ∣ x ) [ log P ( z ∣ x ) ] E_{z\sim Q(z|x)}[\log P(z|x)] Ez∼Q(z∣x)[logP(z∣x)]这同时也是最大似然函数的下界。
三、GAN(生成对抗网络)
1.JS散度
J S D ( P ( x ) ∣ ∣ Q ( x ) ) = 1 2 K L ( P ( x ) ∣ ∣ M ( x ) ) + 1 2 K L ( Q ( x ) ∣ ∣ M ( x ) ) JSD(P(x)||Q(x))=\frac{1}{2}KL(P(x)||M(x))+\frac{1}{2}KL(Q(x)||M(x)) JSD(P(x)∣∣Q(x))=21KL(P(x)∣∣M(x))+21KL(Q(x)∣∣M(x))
其中 M ( x ) = 1 2 ( P ( x ) + Q ( x ) ) M(x)=\frac{1}{2}(P(x)+Q(x)) M(x)=21(P(x)+Q(x)),然后我们对JSD的散度公式进行展开:
J S D ( P ∣ ∣ Q ) = 1 2 ∑ P ( x ) log 2 P ( x ) P ( x ) + Q ( x ) + 1 2 ∑ Q ( x ) log 2 Q ( x ) P ( x ) + Q ( x ) = 1 2 ∑ P ( x ) log P ( x ) P ( x ) + Q ( x ) + 1 2 ∑ Q ( x ) log Q ( x ) P ( x ) + Q ( x ) + log 2 \begin{equation}\nonumber \begin{aligned} JSD(P||Q)&=\frac{1}{2}\sum P(x)\log \frac{2P(x)}{P(x)+Q(x)}+\frac{1}{2}\sum Q(x)\log \frac{2Q(x)}{P(x)+Q(x)}\\ &=\frac{1}{2}\sum P(x)\log \frac{P(x)}{P(x)+Q(x)}+\frac{1}{2}\sum Q(x)\log \frac{Q(x)}{P(x)+Q(x)}+\log 2 \end{aligned} \end{equation} JSD(P∣∣Q)=21∑P(x)logP(x)+Q(x)2P(x)+21∑Q(x)logP(x)+Q(x)2Q(x)=21∑P(x)logP(x)+Q(x)P(x)+21∑Q(x)logP(x)+Q(x)Q(x)+log2

我们可以看到两个分布会在某些点上没有重叠,这时候 P ( x ) 和 Q ( x ) P(x)和Q(x) P(x)和Q(x)一定有一个值接近于0,所以JS散度的值会一直保持在log2,这就会导致一个问题,只要两个分布之间存在距离,函数的输出值是一个常数,无法进行梯度下降更新参数。

- JS散度与KL散度相比的优点:
JS散度的值域范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更确切了。
并且JS散度满足了交换性,克服了KL散度不满足交换性的结果。
2.Wasserstein距离
1.Wasserstein距离简介
Wasserstein距离也叫做推土机距离(Earth Mover’s distance),它从一个分布转换成另外一个分布的过程十分像挖土搬土的过程
2.为什么要使用Wassertain距离?
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近;
KL散度和JS散度是突变的,要么最大要么最小,Wasserstein距离却是平滑的,使用梯度下降法时,KL散度与JS散度都无法计算梯度,而Wassertain距离可以计算梯度
Wasserstein disatnce 的缺点是计算量过大,所以难于计算
3.Wassertain距离的公式推导
我们期望将p(x)分布转化为q(x),那我们假设联合分布为 γ ( x , y ) \gamma(x,y) γ(x,y),转移成本为 d ( x , y ) d(x,y) d(x,y),我们的目的是要找出其最短的Wassertain距离。
W [ p , q ] = inf γ ∈ ∏ [ p , q ] ∬ γ ( x , y ) d ( x , y ) d x d y W[p,q]=\inf_{\gamma \in \prod [p,q]} \iint \gamma(x,y)d(x,y)dxdy W[p,q]=γ∈∏[p,q]inf∬γ(x,y)d(x,y)dxdy
s . t . { ∫ γ ( x , y ) d y = p ( x ) ∫ γ ( x , y ) d x = q ( y ) γ ( x , y ) ≥ 0 \begin{equation} s.t. \begin{cases} %实现分段函数 \int \gamma(x,y) dy =p(x)\\ \int \gamma(x,y) dx =q(y)\\ \gamma(x,y) \geq0 \end{cases} \end{equation} s.t.⎩ ⎨ ⎧∫γ(x,y)dy=p(x)∫γ(x,y)dx=q(y)γ(x,y)≥0
为了简化计算,我们可以将约束条件与原式子进行整合,并且找出其对偶问题,我们就设两个对偶函数分别为 f ( x ) f(x) f(x)与 g ( y ) g(y) g(y)
W [ p , q ] = inf γ [ x , y ] ≥ 0 ∬ γ ( x , y ) d ( x , y ) d x d y + ∫ f ( x ) [ p ( x ) − ∫ γ ( x , y ) d y ] d x + ∫ g ( y ) [ q ( y ) − ∫ γ ( x , y ) d x ] d y W[p,q]=\inf_{\gamma[x,y] \geq 0} \iint \gamma(x,y)d(x,y)dxdy + \int f(x) [p(x) - \int\gamma(x,y) dy ]dx\\+\int g(y) [q(y) -\int \gamma(x,y) dx]dy W[p,q]=γ[x,y]≥0inf∬γ(x,y)d(x,y)dxdy+∫f(x)[p(x)−∫γ(x,y)dy]dx+∫g(y)[q(y)−∫γ(x,y)dx]dy
通过整理得到该距离公式为:
W [ p , q ] = inf γ [ x , y ] ≥ 0 ∬ γ ( x , y ) [ d ( x , y ) − f ( x ) − g ( y ) ] d x d y + ∫ f ( x ) p ( x ) d x + ∫ g ( y ) q ( y ) d y W[p,q]=\inf_{\gamma[x,y] \geq 0} \iint \gamma(x,y)[d(x,y)-f(x)-g(y)]dxdy \\+ \int f(x) p(x)dx+\int g(y) q(y)dy W[p,q]=γ[x,y]≥0inf∬γ(x,y)[d(x,y)−f(x)−g(y)]dxdy+∫f(x)p(x)dx+∫g(y)q(y)dy
由于我们需要求最小距离,那么我们在知道 γ ( x , y ) ≥ 0 \gamma(x,y) \geq 0 γ(x,y)≥0的情况下,必须要保证 [ d ( x , y ) − f ( x ) − g ( y ) ] ≤ 0 [d(x,y)-f(x)-g(y)]\leq0 [d(x,y)−f(x)−g(y)]≤0,从而引出我们的对偶问题:
W [ p , q ] = [ sup f , g ∫ [ f ( x ) p ( x ) + g ( x ) q ( x ) ] d x ∣ d ( x , y ) ≥ f ( x ) + g ( y ) ] W[p,q]=[\sup_{f,g} \int [f(x) p(x)+g(x) q(x)]dx \quad \vert \quad d(x,y)\geq f(x)+g(y)] W[p,q]=[f,gsup∫[f(x)p(x)+g(x)q(x)]dx∣d(x,y)≥f(x)+g(y)]
然后我们的距离公式一般取值为 d(x,y) = ∣ ∣ x − y ∣ ∣ ||x-y|| ∣∣x−y∣∣
3.GAN的优缺点
- 优点:
- GAN避免了马尔科夫链式的学习机制(状态转移矩阵),只用到了反向传播,提高了GAN的效率。
- GAN是一个非常灵活的设计框架,各种类型的损失函数都可以整合到GAN模型当中,理论上只要可微函数都能用于构建生成器和判别器。这样使得针对不同的任务,我们可以设计不同类型的损失函数,都可以在GAN的框架下进行学习和优化。
- 当概率密度不可计算的时候,传统的一些生成模型就不可以工作了。但是GAN在这种情况下依然可以使用,这是因为GAN引入了一个非常聪明的内部对抗的训练机制,可以逼近一些不是很容易计算的目标函数。
- 不依赖任何先验假设。许多方法会假设数据服从某一分布,然后使用极大似然去估计数据分布。
- 采用了生成对抗网络,可以使产生出来的图片更加清晰。
- 缺点:
- 训练GAN需要达到纳什均衡,有时候可以用梯度下降法做到,有时候做不到
- 它很难去学习生成离散的数据,就像文本
- GAN的可解释性非常差
4.GAN的应用领域
GAN的应用领域十分的多,接下来将会挑几个展示一下:
5.GAN的基本组成
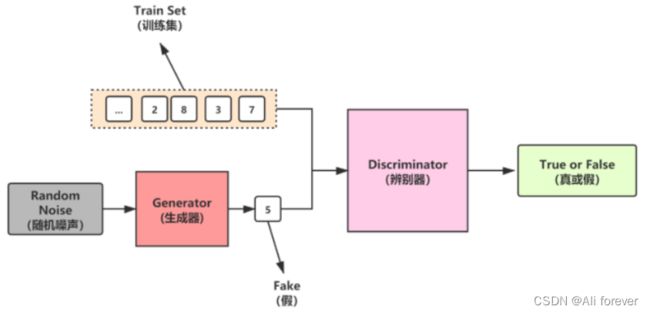
我们可以看到GAN有两个网络,分别是Generator(生成器)和Discriminator(判别器)组成,GAN的输入是一个随机噪声。
- 生成网络:
让随机噪声作为输入,通过生成器尝试输出逼近真实分布的图像,目标是使判别网络误以为该图像为真实图像。 - 判别网络:
判别网络的输入为真实图像或生成图像,并判别该图像是否为真实图像,目标是尽最大可能将生成图像识别出来,输出的标量越大越真。当辨别器无法分辨真假,即判别概率为0.5时,停止训练。
6.GAN的训练过程
- 初始化生成器G和辨别器D两个网络的参数。
- 从训练集抽取n个样本,以及生成器利用定义的噪声分布生成n个样本。固定生成器G,训练辨别器D,使其尽可能区分真假。
- 循环更新k次辨别器D之后,更新1次生成器G,使辨别器尽可能区分不了真假。
- 多次更新迭代后,理想状态下,最终辨别器D无法区分图片到底是来自真实的训练样本集合,还是来自生成器G生成的样本即可,此时辨别的概率为0.5,完成训练。
7.GAN的优化
我么前面讲过,可以采用散度这一个数学概念来衡量两个分布之间的距离,GAN生成器中产生的图片与我们真实数据集里面产生的图片其实来源于两个不同的分布,所以我们去进行优化的时候,恰恰也可以利用散度这一个概念去进行优化迫近

可以看到,我们设生成器产生的分布为 P G P_G PG,数据集中抽取的分布为 P d a t a P_{data} Pdata,那么我们想要获取更好的生成器就需要:
G ∗ = arg min G D i v ( P G , P d a t a ) G^*=\arg \min_G Div(P_G,P_{data}) G∗=argGminDiv(PG,Pdata)
前面我们也说过,判别器中,我们需要固定生成器,从而使判别器的输出达到最大,这样就能分辨出生成图片了,下面V函数表征的意思是指分别从数据集Data和生成器G中抽取出的数据之间的距离。

D ∗ = arg max D V ( D , G ) D^*=\arg \max_DV(D,G) D∗=argDmaxV(D,G)
其中 V ( G , D ) = E y ∼ P d a t a [ log D ( y ) ] + E y ∼ P G [ log ( 1 − D ( y ) ) ] V(G,D)=E_{y\sim P_{data}}[\log D(y)]+E_{y\sim P_{G}}[\log(1- D(y))] V(G,D)=Ey∼Pdata[logD(y)]+Ey∼PG[log(1−D(y))]
后面计算的过程相对来说比较复杂,所以我们直接给出结论:
max D V ( D , G ) = − 2 log 2 + 2 J S D ( P d a t a ∣ ∣ P G ) \max_DV(D,G) =-2\log2 + 2JSD(P_{data}||P_G) DmaxV(D,G)=−2log2+2JSD(Pdata∣∣PG)
这样我们发现每次我们更新参数时,得出的结果是一个常数(因为JS散度在两分布没有交集时一直为0),这样我们将无法更新我们的参数去调整我们的模型。
8.WGAN
所以我们利用前面讲过的Wassertain距离引入了一种方法:WGAN,这种方法有效地抑制了JS散度带来的问题。其中加的Lipschitz限制是防止每次变化过大,导致结果不收敛。要保证D平滑地进行优化

max D ∈ 1 − L i p s c h i t z [ E y ∼ P d a t a D ( y ) − E y ∼ P G D ( y ) ] \max_{D \in1-Lipschitz}[E_{y\sim P_{data}} D(y)-E_{y\sim P_{G}} D(y)] D∈1−Lipschitzmax[Ey∼PdataD(y)−Ey∼PGD(y)]
事实上Lipschitz函数是这样的:

需要满足函数的输出值的变化量小于等于K倍的输入变化量。
除此之外我们有一种进阶版的WGAN(WGAN-GP),它利用限制条件的转化构成新的模型从而达到效果。
max D ( E y ∼ P d a t a D ( y ) − E y ∼ P G D ( y ) − λ E y ∼ P p e n a l t y [ m a x ( 0 , ( ∣ ∣ ∇ x D ( x ) ∣ ∣ − 1 ) ] ) \max_D (E_{y\sim P_{data}} D(y)-E_{y\sim P_{G}} D(y)-\lambda E_{y\sim P_{penalty}}[max(0,(||\nabla_x D(x)||-1)]) Dmax(Ey∼PdataD(y)−Ey∼PGD(y)−λEy∼Ppenalty[max(0,(∣∣∇xD(x)∣∣−1)])
其中我们的 y ∼ P p e n a l t y y\sim P_{penalty} y∼Ppenalty是指中间的一个连通域

那么我们如何从GAN转换成WGAN呢?
- 将我们判别器训练中的 log D ( x ) \log D(x) logD(x)换成 D ( x ) D(x) D(x)
- 去除sigmoid函数,因为我们的penalty是线性函数
- 设置我们的weight clipping或者是penalty
- 将我们生成器训练中目标函数修改成下面这样
9.Mode Collapse(模式塌陷)
所谓Mode Collapse(模式坍塌),指的是生成器产生的结果很单一,仅仅只是为了得到最低的判别器损失,却忽视了数据集的分布,这会出现GAN训练生成出来的结果来来去去都是那几个东西。

出现Mode Collapse的原因在数学上十分复杂,简单来说是为了更快的收敛,生成器会倾向于生成一些已经骗过判别器的样本,这样就会像上面一样,一直围绕着一颗星附近进行生成。
10.Mode Dropping
所谓Mode Dropping,指 GAN 能很好地生成训练集中的数据,但难以生成非训练集的数据,“缺乏想象力”。因为采样数量的局限性,现实中我们无法采集到全部可能的图像,所以一般采集一定数量的图像来代表整个图像分布。

事实上,数据集不能代表整个分布,但是训练时误以为就是整个分布,导致训练来训练去都逃不开这个数据集,导致一定的过拟合。最后的结果就是无论怎么训练,结果都是极其相似的结果,并且很多都是数据集中的内容。
四、其他的GAN网络
1.Conditional GAN(条件生成对抗网络)
在传统的GAN中,我们输入到生成器G里面的是随机噪声,所以模型无法控制正在生成的数据的模式,这样在判别器中有很多图片可能只是清晰度不够却被判了差的结果,评判的标准不好。但是,通过将附加信息作为条件条件化(conditioning)模型,可以指导数据生成过程。这种条件化可以基于类标签,也可以基于图像修复数据的一部分。
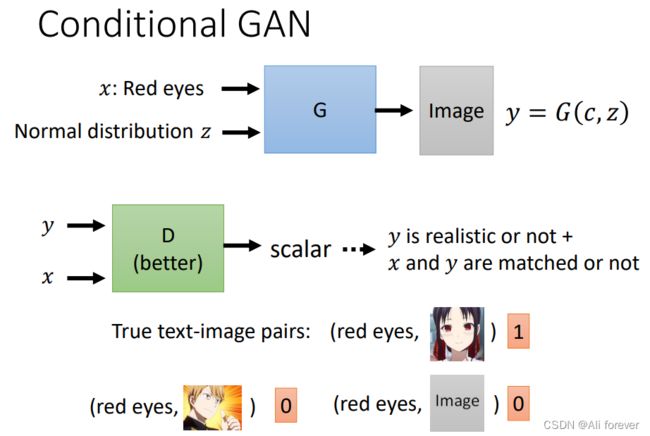
我们可以看到在Conditional GAN中,我们在生成器中的输入加入了一个特征数据,并且在判决器中也同样加入了同样一个x,这样的输出就不止是0或者1这种单调低效的判别标准,同时还有red eyes这一个输出,观察是否与输入的特征值匹配,增加了判别的多样性与准确性。
事实上Conditioanl GAN可以用在很多方面:text-to-image,image-to-image都是可以的。
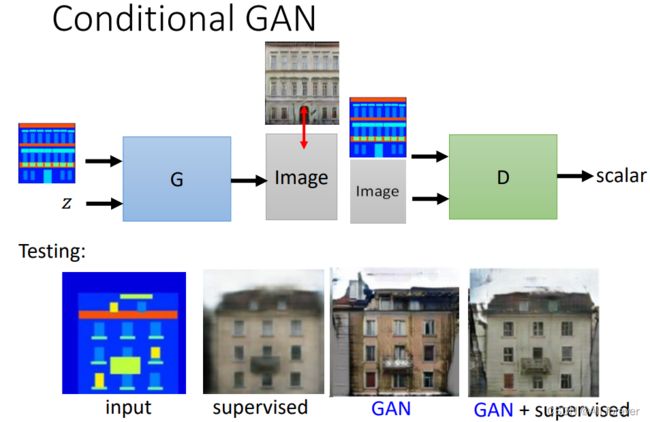
利用监督学习生成的图片是比较模糊的,我们可以将其与我们的Conditonal GAN结合在一起,那么我们训练之后,就会得到比较清晰的图片。
2.Cycle GAN(循环生成对抗网络)
当我们的数据集中,如果输入输出的数学是不成对出现的,那么我们训练出来的结果将很难与输入结果进行匹配,那么就需要引出我们的另外一种GAN网络:Cycle GAN
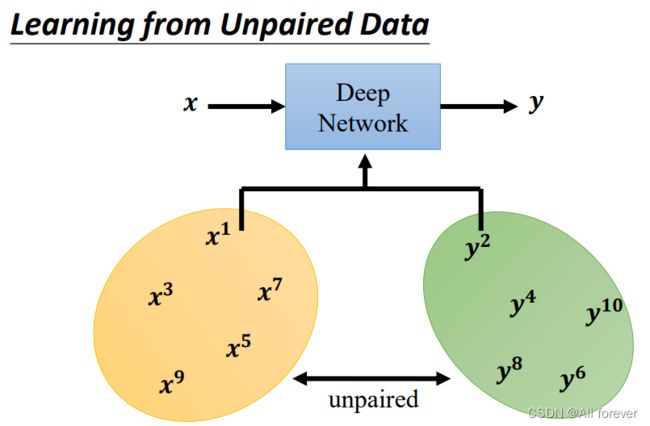
所谓的Cycle GAN,其实本质上就是通过一个循环,首先将图像从一个域转换到另一个域,然后,再转回来,如果两次转换都很精准的话,那么,转换后的图像应该与输入的图像基本一致。通过这样的的一个循环,CycleGAN将转换前后图片的配对,类似于监督学习,提升了转换效果。

在Cycle GAN,我们必须要有两个生成器,第一个生成器将原图转换成目标图,第二个生成器是为了避免在判决器时出现清晰图片蒙混过关的问题时(由于是不配对的图片,所以无法使用前面的conditional GAN),将已经生成的图片重新生成原图,这样本质上其实完成了一次匹配。
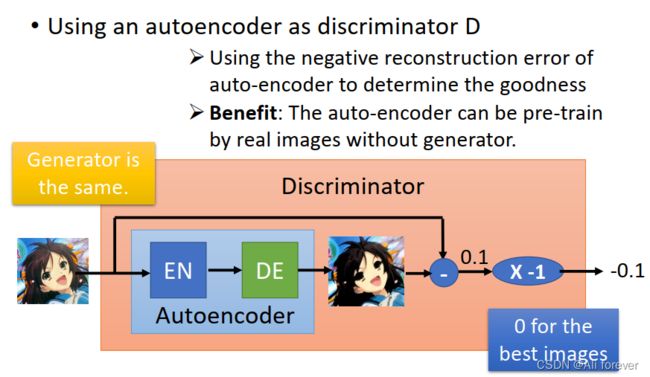
3.Energy-based GAN (EBGAN)
这种GAN模型,将我们的判别器换成了一个Autoencoder,这就允许了判别器可以进行预训练(不需要利用真实的照片),大大提高了判别器的训练速度。