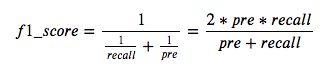7 机器学习 逻辑回归 分类模型的评价指标 混淆矩阵
机器学习
1 逻辑回归
1.1 引入
回归模型是用来处理连续型标签样本的算法模型。
逻辑回归(Logistic Regression)模型广泛应用于分类问题中,尤其是二分类问题。
1.1.1 线性回归
线性回归用于寻找样本数据中特征与标签之间的关系,一般标签数据是连续的,而且特征与标签之间的关系是线性的。
z = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n z = [ θ 0 θ 1 θ 2 . . . θ n ] [ x 0 x 1 x 2 . . . x n ] = θ T x \begin{aligned} z =& \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n \\[3ex] z =& \begin{bmatrix} \theta_0 & \theta_1 & \theta_2 & ... & \theta_n \end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ ... \\ x_n \\ \end{bmatrix} = \boldsymbol{\theta}^T\boldsymbol{x} \end{aligned} z=z=θ0+θ1x1+θ2x2+...+θnxn[θ0θ1θ2...θn]⎣⎢⎢⎢⎢⎡x0x1x2...xn⎦⎥⎥⎥⎥⎤=θTx
1.1.2 回归模型处理分类问题
线性回归模型处理的一般是预测问题,通过样本的特征数据计算出标签数据,样本的特征数据和标签数据之间一般呈线性关系,且标签数据是连续的。
需要对线性回归模型进行改进,使其能够处理二分类问题。
线性回归模型输出的是连续型数据,因此可以设定一个阈值,如果模型输出结果大于这个阈值,则将样本划分到一个标签类别中,反之将样本划分到另一个标签类别中,采用这种方法建立模型也可以称为感知机(Perceptron)。
如果对线性回归模型输出的连续型数据进行归一化处理,使其在0至1之间连续分布,阈值的取值范围就能确定了。对于二分类问题,阈值一般设置为0.5。
可以使用Sigmoid函数对线性回归模型的输出值进行处理,这样建立的模型称为逻辑回归模型。
1.2 逻辑回归模型
1.2.1 Sigmoid函数
Sigmoid函数是一种S型函数,将变量映射到0到1之间。
Sigmoid函数可用于归一化,与sklearn提供的MinMaxSclaer区别是
经过MinMaxScaler归一化处理后的数据可以取到边界0和1,而Sigmoid函数只能无限逼近0和1。
S ( x ) = 1 1 + e − x S(x) = {1 \over {1 + e^{-x}}} S(x)=1+e−x1
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def sigmoid(z):
return 1 / (1 + np.exp(-z))
x = np.arange(-10, 10, step=0.1)
sig_x = sigmoid(x)
plt.figure(figsize=(9, 6))
plt.plot(x, sig_x)
plt.axvline(0, c='black', ls=':')
plt.axhline(y=.5, color='.3',alpha=1.0, ls=':')
plt.axhspan(.0, 1.0, facecolor='0.9', alpha=1.0, ls=':', edgecolor='0.4')
plt.yticks([.0, .5, 1.0])
1.2.2 逻辑回归模型的预测函数
Sigmoid函数可以将实数映射到0至1之间,可用于将值函数转换为更适合处理二分类问题的函数。
将线性回归方程作为变量与Sigmoid函数进行结合。
g ( z ) = 1 1 + e − z z = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n = θ T x g(z) = {1 \over {1 + e^{-z}}} \\[1em] z = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n = \boldsymbol{\theta}^T\boldsymbol{x} g(z)=1+e−z1z=θ0+θ1x1+θ2x2+...+θnxn=θTx
得到逻辑回归模型的预测函数
g ( x ) = y ( x ) = 1 1 + e − θ T x g(x) = y(x) = {1 \over {1 + e^{-\boldsymbol{\theta}^T\boldsymbol{x}}}} g(x)=y(x)=1+e−θTx1
y ( x ) y(x) y(x)是逻辑回归模型的输出值,取值范围为 ( 0 , 1 ) (0, 1) (0,1)。
逻辑回归模型输出值为0至1之间的连续值,可以直接将输出值视为分类概率。
1.2.3 形似几率odds
形似几率odds:正例样本概率与负例样本概率的比值,也可以理解为相对概率,在二分类问题中
o d d s = p 1 − p odds = {p \over {1 - p}} odds=1−pp
对逻辑回归模型的预测函数取形似几率,再进行取对数处理。
l n y ( x ) 1 − y ( x ) = l n ( 1 1 + e − θ T x 1 − 1 1 + e − θ T x ) = θ T x ln{y(x) \over {1 - y(x)}} = ln({{1 \over {1 + e^{-\boldsymbol{\theta}^T\boldsymbol{x}}}} \over {1 - {1 \over {1 + e^{-\boldsymbol{\theta}^T\boldsymbol{x}}}}}}) = \boldsymbol{\theta}^T\boldsymbol{x} ln1−y(x)y(x)=ln(1−1+e−θTx11+e−θTx1)=θTx
可以发现,逻辑回归输出值的形似几率取对数后就是线性回归的输出值。
因此,逻辑回归是由线性回归变化而来的。逻辑回归的形似几率取对数是线性回归。
1.2.4 逻辑回归模型的工作过程
构建线性回归模型是通过求解θ参数矩阵构建预测函数,目标是预测函数尽可能地拟合数据。
构建逻辑回归模型也是通过求解θ参数矩阵构建一个尽可能拟合数据的预测函数,并通过向预测函数中输入样本的特征矩阵来获取样本的在各个标签的分类概率。
处理逻辑回归问题时,不管原始样本中的类别特征任何值或者文字表示,逻辑回归模型统一将特征值视为0和1。

1.2.5 逻辑回归模型的优点
逻辑回归模型是一个使用广泛的模型。
- 逻辑回归对线性样本数据(特征与标签之间存在很强的线性关系)的拟合效果非常好。
金融领域中的信用卡欺诈,评分卡制作,电商领域中的营销预测等问题都是逻辑回归模型的强项。
相对,逻辑回归模型处理非线性数据的效果很差,如果已知待处理的样本数据是非线性的,不要使用逻辑回归。
判别一个模型是否为线性的,只需要判别决策边界是否是直线,即是否能用一条直线来划分。 - 逻辑回归计算速度快。
对于线性数据,逻辑回归的拟合和计算速度都非常快,计算效率优于SVM和随机森林等。 - 逻辑回归模型返回的分类结果不是固定的0或1,而是分类的概率,因此可以将逻辑回归返回的结果当作连续型数据来使用。
比如在评分卡制作时,我们不仅需要判断客户是否会违约,还需要给出确定的”信用分值“,计算信用分值就需要使用分类概率计算出的对数概率 。
1.3 逻辑回归模型的损失函数
1.3.1 损失函数
逻辑回归模型主要用于处理二分类问题,使用的损失函数是对数似然损失函数。
正例:y=1
负例:y=0

− l o g ( h θ ( x ) ) -log(h_\theta(x)) −log(hθ(x)) 表示划分到正例(y=1)类别的损失值;
− l o g ( 1 − h θ ( x ) ) -log(1-h_\theta(x)) −log(1−hθ(x)) 表示划分到正例(y=0)类别的损失值。
如果模型的预测结果 h θ ( x ) h_\theta(x) hθ(x)接近1,
- − l o g ( h θ ( x ) ) -log(h_\theta(x)) −log(hθ(x))非常小,表示划分到正例(y=1)类别的损失值非常小;
- − l o g ( 1 − h θ ( x ) ) -log(1-h_\theta(x)) −log(1−hθ(x))非常大,表示划分到负例(y=0)类别的损失值非常大。
1.3.2 梯度下降
可以使用梯度下降(Gradient Descent)法找到合适的参数,使损失函数J()最小化。
梯度下降是一种迭代法,从给定的起始点开始,沿着函数按照负梯度的方向不断移动指定步长,尝试找到函数的最小值。
1.3.3 正则化
如果过度追求损失函数的最小值,可能会导致模型出现过拟合问题。出现过拟合的现象是,在样本训练集损失函数非常小,表现非常好,当在测试集中模型的损失函数非常大,即模型处理新数据时表现非常差。
可以解决正则化处理过拟合问题。
正则化本质上就是在损失函数的后面添加惩罚项,惩罚项一般由参数的L1范式或L2范式组成。通过引入惩罚项来矫正损失函数,从而修正了模型的参数。
- L1正则化
在L1正则化在逐渐加强的过程中,携带信息量小的、对模型贡献不大的特征的参数w,会比携带大量信息的、对模型有巨大贡献的特征的参数更快地变成0,所以L1正则化本质是一个特征选择的过程。L1正则化越强,参数向量中就越多的参数为0,选出来的特征就越少,以此来防止过拟合。因此,如果特征量很大,数据维度很高,我们会倾向于使用L1正则化。
L1范式是参数向量中的每个元素的绝对值之和。
J ( θ ) L 1 = J ( θ ) + 1 C ∑ j = 1 n ∣ θ j ∣ ( j ≥ 1 ) J(\theta)_{L1}=J(\theta)+{1 \over C}\sum^n_{j=1}|\theta_j| \quad (j \geq 1) J(θ)L1=J(θ)+C1j=1∑n∣θj∣(j≥1)
式中,J()表示损失函数,n是模型的特征数量,等于参数向量的长度,C是用来控制正则化程度的超参数,C越小,惩罚项产生的损失就越大,表示正则化的效力越强,使得参数逐渐被压缩得越来越小。 - L2正则化
L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大的特征的参数w会非常接近于0。通常来说,如果我们的主要目的只是为了防止过拟合,选择L2正则化就足够了。但是如果选择L2正则化后还是过拟合,模型在未知数据集上的效果表现很差,就可以考虑L1正则化。
L2范式是参数向量中的每个元素平方和的开方值。
J ( θ ) L 2 = J ( θ ) + 1 C ∑ j = 1 n ( θ j ) 2 ( j ≥ 1 ) J(\theta)_{L2}=J(\theta)+{1 \over C} \sqrt{\sum^n_{j=1} (\theta_j)^2} \quad (j \geq 1) J(θ)L2=J(θ)+C1j=1∑n(θj)2(j≥1)
import numpy as np
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
# 加载样本数据
data = load_breast_cancer()
X = data.data
y = data.target
# 建立两种模型
lrl1 = LR(penalty="l1", C=0.1, solver='liblinear')
lrl2 = LR(penalty="l2", C=0.1, solver='liblinear')
# 逻辑回归的重要属性coef_,查看每个特征所对应的参数
lrl1.fit(X, y)
print('L1范式:', lrl1.coef_)
'''
L1范式:
[[ 0.57970932 0. 0.26093095 -0.00467821 0. 0.
0. 0. 0. 0. 0. 0.
0. -0.04937868 0. 0. 0. 0.
0. 0. 0.46133689 -0.13130097 -0.14380568 -0.01999359
0. 0. 0. 0. 0. 0. ]]
'''
lrl2 = lrl2.fit(X, y)
print('L2范式:', lrl2.coef_)
'''
L2范式:
[[ 0.66541082 0.08750769 0.31057879 -0.01110079 -0.02466001 -0.11248162
-0.15946592 -0.06862043 -0.03431566 -0.00637208 0.02489405 0.28687305
0.06586186 -0.07477127 -0.00238889 -0.0218438 -0.03156067 -0.00886403
-0.00808669 -0.00185966 0.67946821 -0.22842667 -0.21219569 -0.01581848
-0.04541302 -0.34636941 -0.4330083 -0.13255881 -0.10933867 -0.03255192]]
'''
1.4 逻辑回归模型代码实现
sklearn.linear_model.LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
超参数解释
- penalty
可以输入l1或者l2来指定使用哪一种正则化方式。不填写默认"l2"。 注意,若选择"l1"正则化,参数solver仅能够使用求解方式”liblinear"和"saga“,若使用“l2”正则 化,参数solver中所有的求解方式都可以使用。 - C
惩罚项。必须是一个大于0的浮点数,不填写默认1.0,即默认正则项与损失函数的比值是1:1。C越小,损失函数会越大,模型对损失函数的惩罚越重,正则化的效力越强,参数会逐渐被压缩得越来越小。 - max_iter
梯度下降中能走的最大步数,默认值为100.步数的不同取值可以帮助我们获取不同的损失函数的损失值。目前没有好的办法可以计算出最优的max_iter的值,一般是通过绘制学习曲线对其进行取值。 - solver
我们之前提到的梯度下降法,只是求解逻辑回归参数的一种方法。sklearn为我们提供了多种选择,让我们可以使用不同的求解器来计算逻辑回归。求解器的选择,由参数"solver"控制,共有五种选择。
liblinear:是二分类专用(梯度下降),也是现在的默认求解器。
lbfgs,newton-cg,sag,saga:是多分类专用,几乎不用。

- multi_class
输入"ovr", “multinomial”, “auto"来告知模型,我们要处理的分类问题的类型。默认是"ovr”。
‘ovr’:表示分类问题是二分类,或让模型使用"一对多"的形式来处理多分类问题。
‘multinomial’:表示处理多分类问题,这种输入在参数solver是’liblinear’时不可用。
“auto”:表示会根据数据的分类情况和其他参数来确定模型要处理的分类问题的类型。比如说,如果数据是二分 类,或者solver的取值为"liblinear",“auto"会默认选择"ovr”。反之,则会选择"multinomial"。 - class_weight
表示样本不平衡处理的参数。样本不平衡指的是在一组数据中,某一类标签天生占有很大的比例,或误分类的代价很高,即我们想要捕捉出某种特定的分类的时候的状况。什么情况下误分类的代价很高?
例如,我们现在要对潜在犯罪者和普通人进行分类,如果没有能够识别出潜在犯罪者,那么这些人就可能去危害社会,造成犯罪,识别失败的代价会非常高,但如果,我们将普通人错误地识别成了潜在犯罪者,代价却相对较小。所以我们宁愿将普通人分类为潜在犯罪者后再人工甄别,但是却不愿将潜在犯罪者 分类为普通人,有种"宁愿错杀不能放过"的感觉。
再比如说,在银行要判断“一个新客户是否会违约”,通常不违约的人vs违约的人会是99:1的比例,真正违约的人其实是非常少的。这种分类状况下,即便模型什么也不做,全把所有人都当成不会违约的人,正确率也能有99%, 这使得模型评估指标变得毫无意义,根本无法达到我们的“要识别出会违约的人”的建模目的。
None:因此我们要使用参数class_weight对样本标签进行一定的均衡,给少量的标签更多的权重,让模型更偏向少数类, 向捕获少数类的方向建模。该参数默认None,此模式表示自动给与数据集中的所有标签相同的权重,即自动1: 1。
balanced:当误分类的代价很高的时候,我们使用”balanced“模式,可以解决样本不均衡问题。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
%matplotlib inline
l2 = []
l2_test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size=0.3, random_state=420)
for i in np.arange(1, 201, 10):
lrl2 = LR(penalty="l2", solver="liblinear", C=0.9, max_iter=i)
lrl2.fit(Xtrain, Ytrain)
# 模型在训练集的表现
l2.append(accuracy_score(lrl2.predict(Xtrain), Ytrain))
# 模型在测试集上的表现
l2_test.append(accuracy_score(lrl2.predict(Xtest), Ytest))
graph = [l2, l2_test]
color = ["black", "red"]
label = ["L2train", "L2test"]
plt.figure(figsize=(20, 5))
for i in range(len(graph)):
plt.plot(np.arange(1, 201, 10), graph[i], color[i], label=label[i])
plt.legend(loc=4)
plt.xticks(np.arange(1, 201, 10))
plt.show()
2 分类模型的评价指标
2.1 混淆矩阵
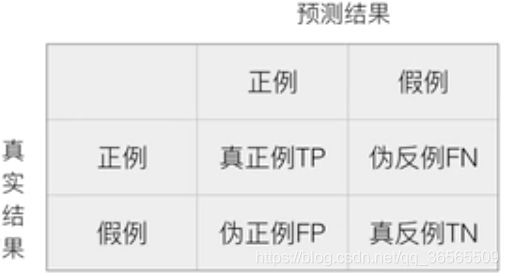
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式。
在分类任务下,预测结果(Predict Condition)和真实结果(True Condition)之间存在的四种不同的组合。适用于二分类和多分类。
例子:设计一个二分类的场景,将图片分类为猫或者狗。
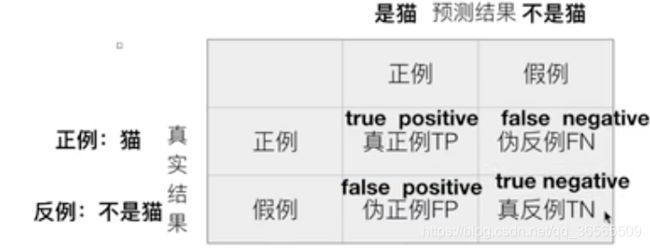
真正例(TP):本来是猫结果预测值为猫的比例(预测为正例是真的)
伪正例(FP):本来不是猫结果预测值为猫的比例(预测为正例是假的)
伪反例(FN):本来是猫结果预测值为不是猫的比例(预测为反例是假的)
真反例(TN):本来不是猫结果预测值为不是猫的比例(预测为反例是真的)
真正例率 TPR = TP / (TP + FN)
预测为正例且实际为正例的样本占所有训练集中为正例样本的比例。
将正例预测对的占正样本的比例(预测对的比例),这个比例越大越好
伪反例率 FPR = FP / (FP + TN)
预测为正例但实际为负例的样本占训练集中所有负例样本的比例
将负例预测错的占负样本的比例(预测错的比例),这个比例越小越好
注意:如果有其他的类别,其他的每一个类别也有其对应的混淆矩阵表示真伪正例和真伪反例的比例。
2.2 准确率
Accuracy = (TP+TN)/(TP+FN+FP+TN)
准确率 = (预测正确) / (预测对的和不对的所有结果),也就是预测正确的比例。
分类问题中模型.score()方法返回的就是模型的准确率。
2.3 召回率(较多被使用)
Recal = TP / (TP+FN)
召回率表示实际为正例的样本(TP+FN)中预测结果为正例(TP)的样本所占比例,也就是正样本有多少被找出来了,召回了多少。
医院预测一个病人是否患有癌症。假设有100个测试样本,包括10个癌症患者,90个非癌症患者,预测结果为6个癌症患者,94个非癌症患者。
召回率就是在10癌症患者中预测正确多少个,或者说在癌症患者中预测出癌症患者的比例
召回率 = 预测出的癌症患者 / 所有癌症患者
API:recall_score
2.4 精确率
Precision = TP / (TP+FP)
预测结果为正例样本(TP+FP)中真实值为正例(TP)的样本所占比例。
例如,本来是猫预测也为猫 /(本来是猫预测也为猫+本来不是猫预测为猫)
API:accuracy_score
2.5 f1-score
有时需要综合精确率和召回率的指标,可以使用f1-score。
模型的精确率和召回率是有矛盾的,而F1分数(F1-score)是分类问题的一个衡量指标。一些多分类问题的机器学习竞赛,常常将F1-score作为最终测评的方法。它是精确率和召回率的调和平均数,最大为1,最小为0。
2.6 AUC
AUC是一个模型评价指标,只能用于二分类模型的评价。
AUC评价指标通常应用的比较多,因为很多机器学习的分类模型计算结果都是概率的形式(比如逻辑回归),那么对于概率而言,我们就需要去设定一个阈值来判定分类,那么这个阈值的设定就会对我们的正确率和准确率造成一定成都的影响。
逻辑回归的默认阈值为0.5
AUC(Area under Curve),表面上意思是曲线下边的面积,这么这条曲线是什么?
ROC曲线(receiver operating characteristic curve,接收者操作特征曲线)
真正例率TPR = TP / (TP + FN)
- 预测为正例且实际为正例的样本占所有训练集中为正例样本的比例。
- 将正例预测对的占正样本的比例(预测对的比例),这个比例越大越好。
伪反例率FPR = FP / (FP + TN)
- 预测为正例但实际为负例的样本占训练集中所有负例样本的比例。
- 将负例预测错的占负样本的比例(预测错的比例),这个比例越小越好。
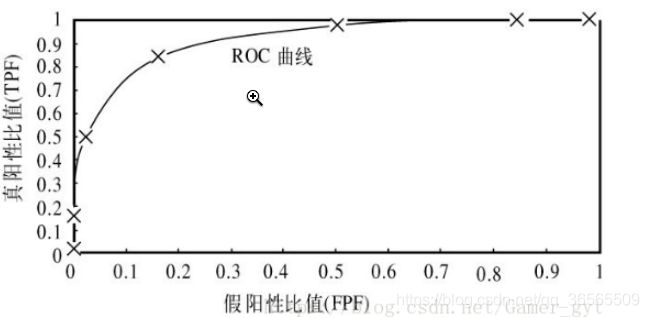
在理想情况下,最佳的分类器应该尽可能地处于左上角,这就意味着分类器在伪反例率(预测错的概率)很低的同时获得了很高的真正例率(预测对的概率)。也就是说ROC曲线围起来的面积越大越好,因为ROC曲线面积越大,则曲线上面的面积越小,则分类器越能停留在ROC曲线的左上角。
AUC的的取值是固定在0-1之间。AUC的值越大越好。
AUC的API
from sklearn.metrics import roc_auc_score
y_pre = predict_proba(x_test) # 返回预测的概率
auc=roc_auc_score(y_test, y_pre[:,1])
import sklearn.datasets as dt
from sklearn.metrics import roc_auc_score, f1_score, recall_score, accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
iris = dt.load_iris()
feature = iris.data
target = iris.target
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2020)
l = LogisticRegression()
l.fit(x_train, y_train)
l.score(x_test, y_test) # 0.8666666666666667
y_pred = l.predict(x_test)
recall_score(y_test, y_pred, average='macro') # 0.8666666666666667
accuracy_score(y_test, y_pred) # 0.8666666666666667
f1_score(y_test, y_pred, average='macro') # 0.8666666666666668