《机器学习》李宏毅P5-8
《机器学习》李宏毅P5-8
- 误差从哪里来
-
- 估测变量的偏差和方差
-
- 偏差(bias)
- 方差
- 偏差与方差对结果的影响
- 不同模型的方差
- 不同模型的偏差
- 偏差v.s.方差
- 模型选择
- 交叉验证
- N-折交叉验证(N-fold Cross Validation)
- 梯度下降(Gradient Desent)
-
- 梯度下降解最优化问题
-
- 调整学习率
-
- 自适应学习率
- 自适应学习率算法——Adagrad
- 随机梯度下降法(SGD)
- 特征缩放
- 梯度下降的理论基础
- 梯度下降的限制
- 作业——预测PM2.5
-
- 作业描述
- 任务要求
- 作业步骤
-
- step1.define function set(model)
- step2.define loss function based on training
- step3.find the best function
- 实际演示
误差从哪里来
根据宝可梦案例,Average ErrorAverage随着模型复杂增加呈指数上升趋势。更复杂的模型并不能给测试集带来更好的效果,而这些 Error的主要有两个来源,分别是 bias和 variance。
机器学习中的Bias(偏差),Error(误差),和Variance(方差)
估测变量的偏差和方差
偏差(Bias)和方差(Variance)——机器学习中的模型选择
偏差(bias)
假设x的平均值是 μ,方差为 σ2
估测平均值时,一般取N个样本点{x1,x2,…xN},计算其平均值可以得到 m = 1 N ∑ n x n ≠ μ m=\frac{1}{N}\sum_{n}{x^n \ne \mu} m=N1∑nxn=μ
但是如果计算很多组的 m,然后求 m 的期望:
 结果刚好等于 μ \mu μ,这个估计就是无偏估计
结果刚好等于 μ \mu μ,这个估计就是无偏估计
m 分布对于 μ \mu μ的离散程度(方差):(N越小越离散)
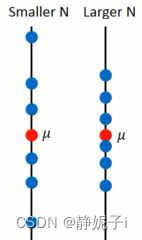
方差
偏差与方差对结果的影响
不同的数据集找到的最优function是不一样的。
不同模型的方差

一次模型的方差就比较小的,也就是是比较集中,离散程度较小。而5次模型的方差就比较大,同理散布比较广,离散程度较大。
所以用比较简单的模型,方差是比较小的。如果用了复杂的模型,方差就很大,散布比较开。
这也是因为简单的模型受到不同训练集的影响是比较小的。
不同模型的偏差
简单的模型函数集的space比较小,所以可能space里面就没有包含靶心,肯定射不中。而复杂的模型函数集的space比较大,可能就包含的靶心,只是没有办法找到确切的靶心在哪,但足够多的数据,就可能得到真正的 function。
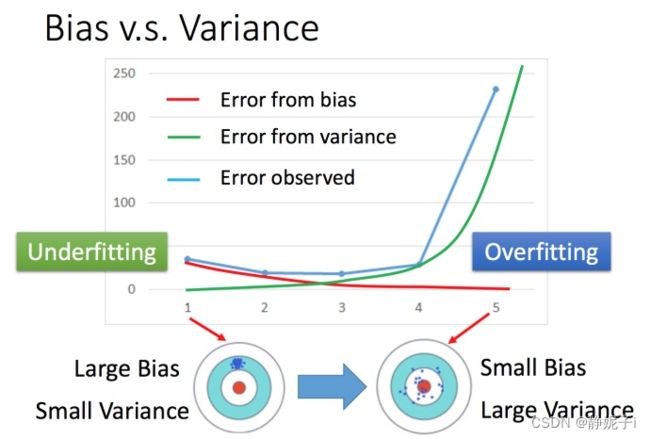
偏差v.s.方差
将系列02中的误差拆分为偏差和方差。简单模型(左边)是偏差比较大造成的误差,这种情况叫做欠拟合,而复杂模型(右边)是方差过大造成的误差,这种情况叫做过拟合。
如果模型没有很好的训练训练集,就是偏差过大,也就是欠拟合
如果模型有很好的训练训练集,即再训练集上得到很小的错误,但在测试集上得到大的错误,这意味着模型可能是方差比较大,就是过拟合。
对于欠拟合和过拟合,是用不同的方式来处理的
偏差大-欠拟合
重新设计模型。因为之前的函数集里面可能根本没有包含目标函数。可以:考虑更多特征,考虑更多次幂、更复杂的模型。 如果此时强行再收集更多的data去训练,这是没有什么帮助的,因为设计的函数集本身就不好,再找更多的训练集也不会更好。
方差大-过拟合
简单粗暴的方法:更多的数据
但是很多时候不一定能做到收集更多的data。可以针对对问题的理解对数据集做调整。比如识别手写数字的时候,偏转角度的数据集不够,那就将正常的数据集左转15度,右转15度,类似这样的处理。
模型选择
在偏差和方差之间需要一个权衡,平衡偏差和方差产生的错误,使得总错误最小
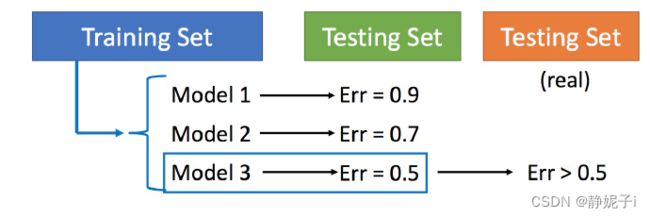
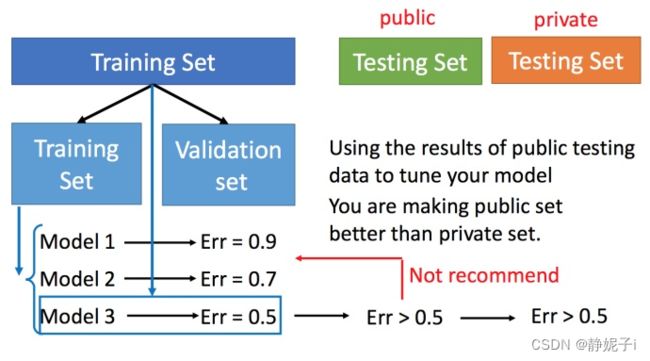
但不能仅仅根据某个测试集的结果做出选择:用训练集训练不同的模型,然后在测试集上比较错误,模型3的错误比较小,就认为模型3好。但实际上这只是你手上的测试集,真正完整的测试集并没有。比如在已有的测试集上错误是0.5,但有条件收集到更多的测试集后通常得到的错误都是大于0.5的。
交叉验证
图中public的测试集是已有的,private是未知的(validate set)。**交叉验证就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集。**用训练集训练模型,然后再验证集上比较,确定最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public的测试集进行测试,此时一般得到的错误都是大一些的。不过此时会比较想再回去调一下参数,调整模型,让在public的测试集上更好,但不太推荐这样。
N-折交叉验证(N-fold Cross Validation)
比如在三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1。
梯度下降(Gradient Desent)
梯度下降解最优化问题
 我们要找一组参数 θ \theta θ ,让损失函数越小越好,这个问题可以用梯度下降法解决
我们要找一组参数 θ \theta θ ,让损失函数越小越好,这个问题可以用梯度下降法解决
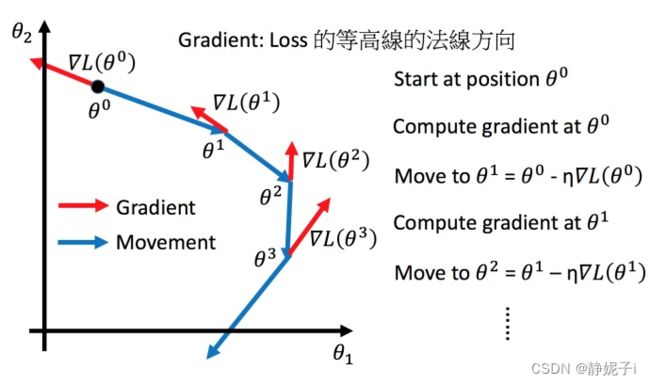
假设 θ \theta θ 有里面有两个参数 θ 1 , θ 2 θ_{1},θ_{2} θ1,θ2, 随机选取初始值 θ 0 = [ θ 1 0 θ 2 0 ] θ^{0}=\left[ \begin{matrix}θ^{0}_{1} \\θ^{0}_{2} \end{matrix} \right] θ0=[θ10θ20]
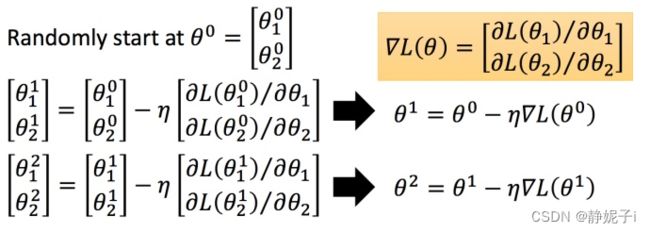
分别计算初始点处,两个参数对 function:L 的偏微分,然后 θ 0 θ^{0} θ0减掉 η 乘上偏微分的值,得到一组新的参数。同理反复进行这样的计算。黄色部分为简洁的写法, ▽ L ( θ ) ▽L(θ) ▽L(θ)即为梯度。
其中:η 叫做Learning rates(学习速率)
调整学习率
- 如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。
- 如果学习率调整的太小,比如蓝色的线,就会走的太慢,时间成本太高。
- 如果学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。
- 还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
可以将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
虽然这样的可视化可以很直观观察,但可视化也只是能在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
自适应学习率
随着次数的增加,通过一些因子来减少学习率。
- 通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
- update好几次参数之后(several epochs),比较靠近最低点了,此时减少学习率
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
自适应学习率算法——Adagrad
w是一个参数
σ t \sigma^t σt :之前参数的所有微分的均方根,对于每个参数都是不一样的。
普通梯度下降如Vanilla Gradient descent
使用Adagrad算法:每个参数的学习率都把除以之前微分的均方根。
举例说明:
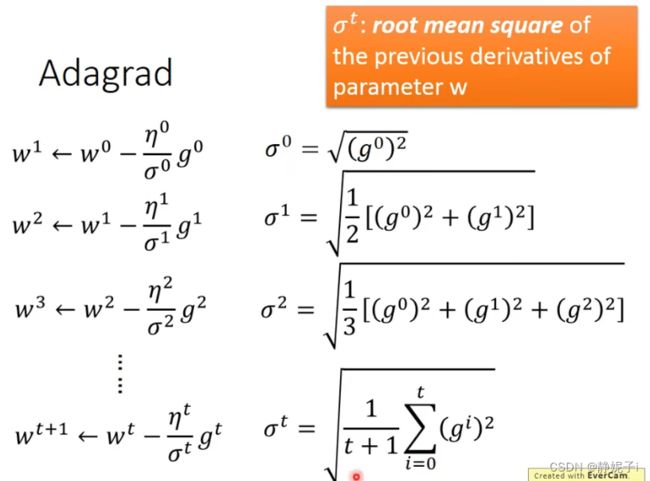 Adagrad最终公式
Adagrad最终公式
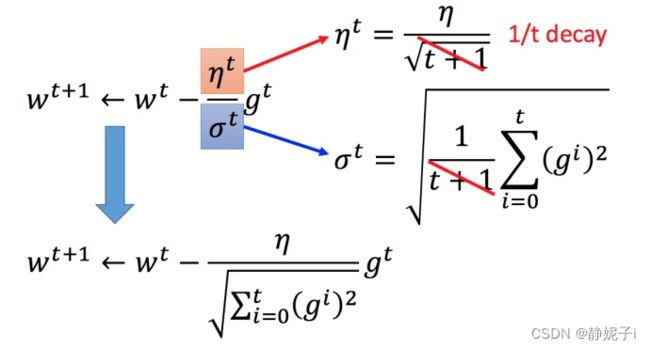 Adagrad矛盾的解释
Adagrad矛盾的解释
根据上述公式可以发现,在 Adagrad 中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。
如何解释这一现象:
直观解释
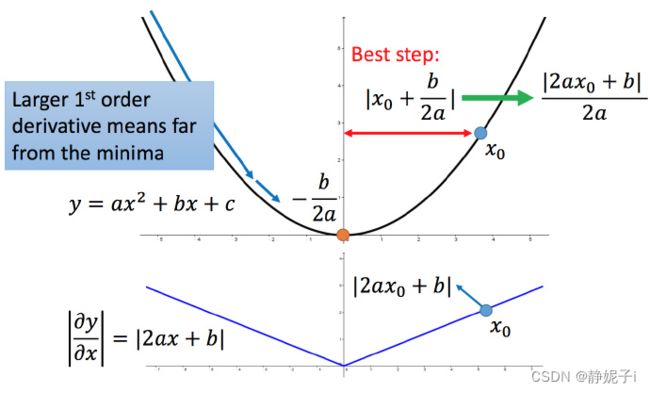
正式解释
比如初始点在 x0,最低点为 -b/2a,最佳的步伐就是 x0到最低点之间的距离 ∣x0+b/2a∣,也可以写成 ∣(2ax0+b)/2a∣而刚好 ∣2ax0+b∣就是方程绝对值在 x0这一点的微分这样可以认为如果算出来的微分越大,则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比,它可能是比较好的。
结论1-1:梯度越大,就跟最低点的距离越远。
但这个结论在多个参数的时候就不一定成立了。
上图左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数 w1,就像图中蓝色的线,得到右边上图结果;如果只考虑参数 w2,就像图中绿色的线,得到右边下图的结果。确实对于 a和 b,结论1-1是成立的,同理 c 和 也成立。但是如果对比a 和 c,就不成立了,c 比 a 大,但 c 距离最低点是比较近的。
所以结论1-1是在没有考虑跨参数对比的情况下,才能成立的。所以还不完善。对function二次微分结果为2a
故最好的结果是:一次微分/二次微分
即不止和一次微分成正比,还和二次微分成反比。最好的step应该考虑到二次微分。
进一步解释
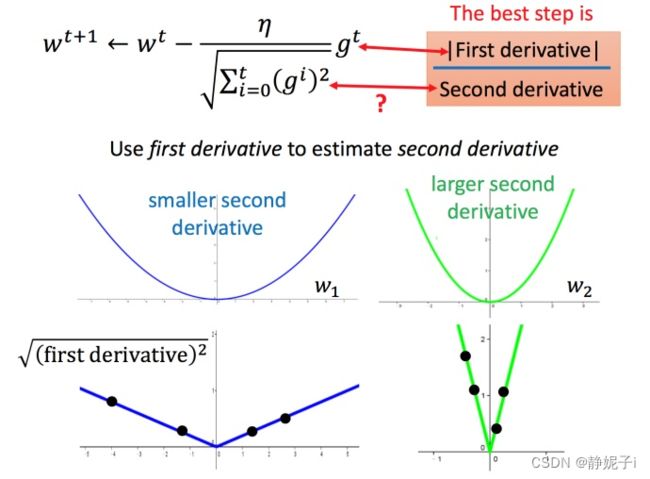 Adagrad除以所有微分均方根:就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)
Adagrad除以所有微分均方根:就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)
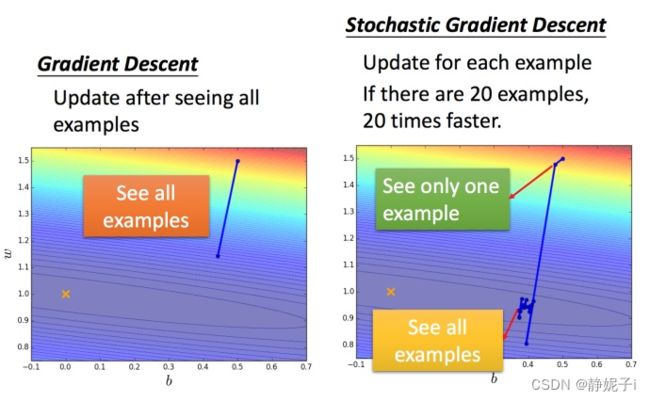
随机梯度下降法(SGD)
损失函数不需要处理训练集所有的数据,选取一个例子 x n x_{n} xn
计算损失函数,就可以update

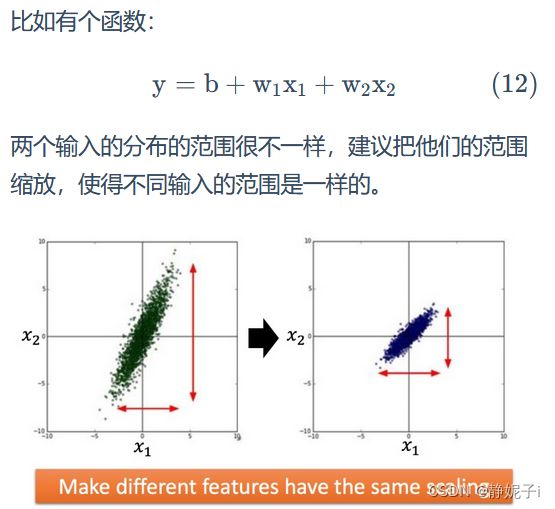
特征缩放
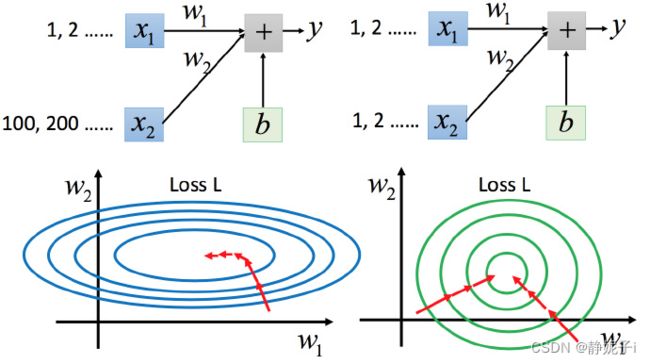
左图: x1的scale比x2要小很多,所以当 w1和 w2做同样的变化时,w1对 y 的变化影响是比较小的(w1对损失函数L有较小的微分,在w1方向上梯度较小,图像较为平滑),x2 对 y 的变化影响是比较大的(w2对损失函数L有较大的微分,在w2方向上梯度较大,图像上有比较陡峭的峡谷)
右图:二者scale相近,各点处梯度大致相同
对于左边的情况,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
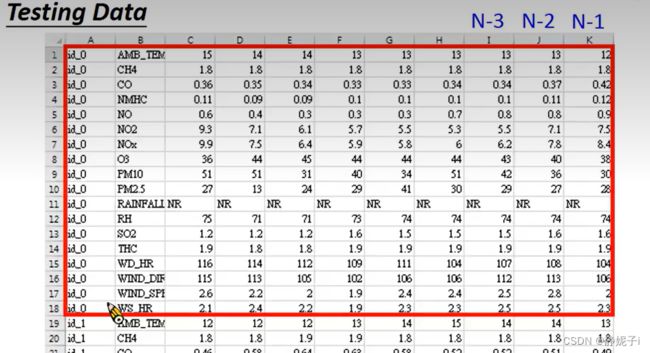
上图每一列都是一个例子,里面都有一组特征。
对每一个维度 i(绿色框)都计算平均数(mi),标准差( σ i σi σi)
用第 r 个例子中的第 i 个输入,减掉平均数 mi,然后除以标准差 σ i σi σi,得到的结果是所有的维数都是 0,所有的方差都是 1
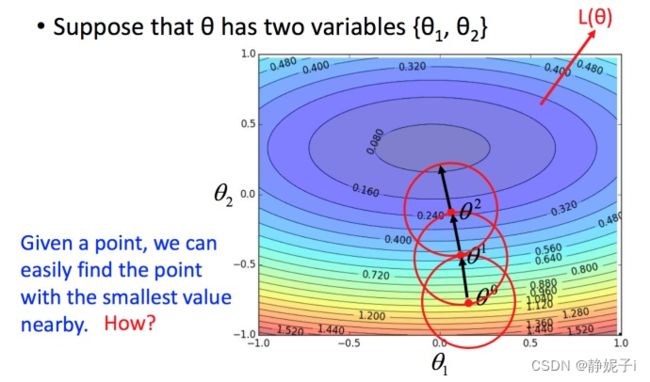
梯度下降的理论基础
已知一个点 θ 0 \theta0 θ0和损失函数:可以在已知点附近找到损失值最小的 θ 1 \theta1 θ1
how to find?
泰勒展开
 两个变量的泰勒展开
两个变量的泰勒展开
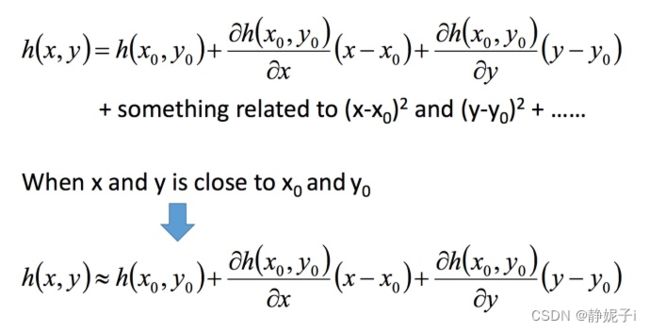
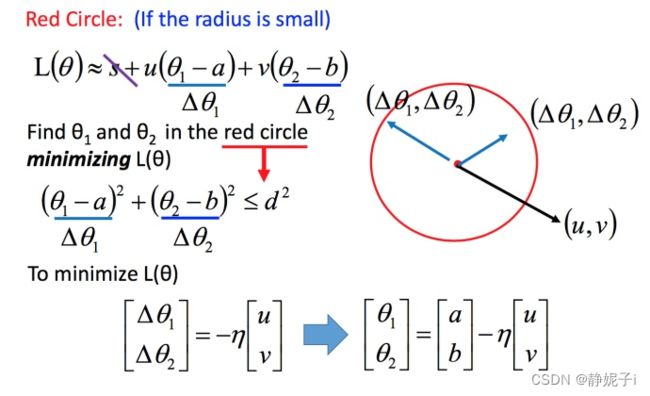
回到之前如何快速在圆圈内找到最小值。基于泰勒展开式,在 (a,b) 点的红色圆圈范围内,可以将损失函数用泰勒展开式进行简化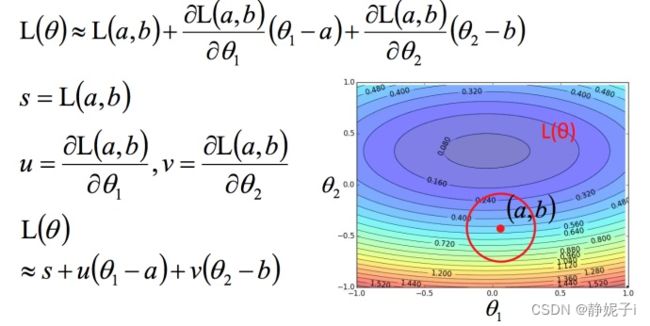 简化为
简化为
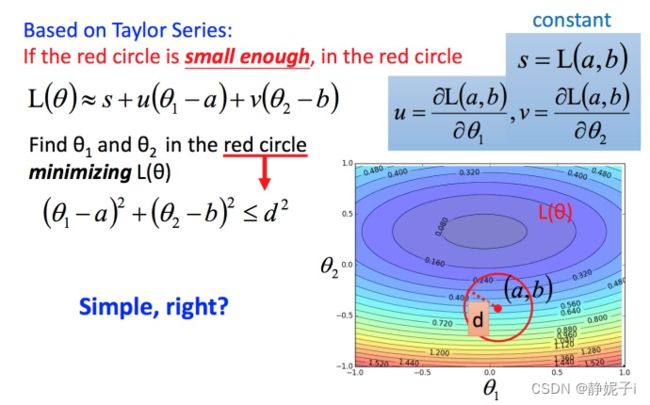 不考虑s的话,可以看出剩下的部分就是两个向量 ( △ θ 1 , △ θ 2 ) (△θ1,△θ2) (△θ1,△θ2)和 ( u , v ) (u,v) (u,v)的内积,那怎样让它最小,就是和向量 (u,v)方向相反的向量
不考虑s的话,可以看出剩下的部分就是两个向量 ( △ θ 1 , △ θ 2 ) (△θ1,△θ2) (△θ1,△θ2)和 ( u , v ) (u,v) (u,v)的内积,那怎样让它最小,就是和向量 (u,v)方向相反的向量
但这里用这种方法找到这个式子有个前提,泰勒展开式给的损失函数的估算值是要足够精确的,而这需要红色的圈圈足够小(也就是学习率足够小)来保证。所以理论上每次更新参数都想要损失函数减小的话,就需要学习率足够足够小才可以。
所以实际中,当更新参数的时候,如果学习率没有设好,是有可能导致做梯度下降的时候,损失函数没有越来越小。
该式考虑了泰勒展开式的一次项,如果考虑到二次项(比如牛顿法),在实际中不是特别好,会涉及到二次微分等,多很多的运算,性价比不好。
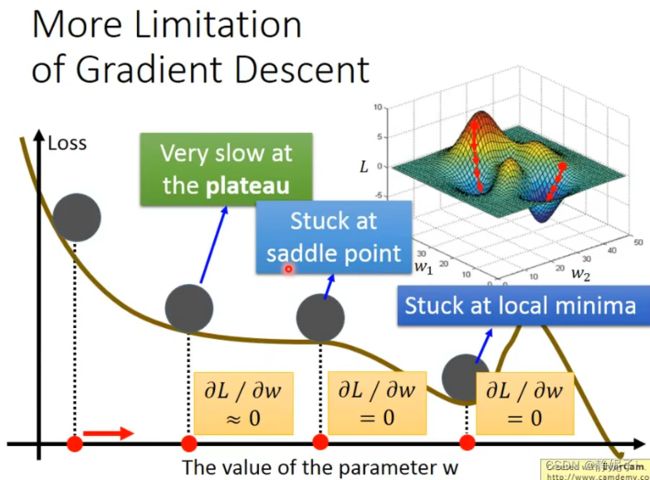
梯度下降的限制
容易陷入局部极值 还有可能卡在不是极值,但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点
作业——预测PM2.5
作业描述
举例: 现在是2017-09-29 8:00:00 ,那么要预测2017-09-29 09:00:00丰原站的PM2.5值会是多少。
评比标准:预测值与实际值的平方误差平均值
预测根据:前9个小时的所有观测数据
任务要求
任务要求:预测PM2.5的值,我们将用梯度下降法 (Gradient Descent) 预测 PM2.5 的值 (Regression 回归问题)
环境要求:要求 python3.5+,只能用numpy,scipy,pandas
- 请用梯度下降手写线性回归
- 最好使用 Public Simple Baseline
数据介绍: 本次作业使用丰原站观测记录,分成 train set 跟 test set,train set 是丰原站每個月的前20天所有资料,test set则是从丰原站剩下的资料中取样出来。 train.csv:每个月前20天每个小時的气象资料(每小时有18种)。共12个月。 test.csv:从剩下的资料当中取样出连续的10小时为一笔,前九小时的所有观测数据当作feature,第十小时的PM2.5当作answer。一共取出240笔不重复的 test data,请根据feauure预测这240笔的PM2.5。
作业步骤
step1.define function set(model)
step2.define loss function based on training
step3.find the best function
梯度下降
实际演示
数据预处理
#-*- coding:utf-8 -*-
# @File : PM2.5Prediction.py
# @Date : 2019-05-19
# @Author : 追风者
# @Software: PyCharm
# @Python Version: python 3.6
'''
利用线性回归Linear Regression模型预测 PM2.5
特征工程中的特征选择与数据可视化的直观分析
通过选择的特征进一步建立回归模型
'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
'''数据读取与预处理'''
# DataFrame类型
train_data = pd.read_csv("./Dataset/train.csv")
train_data.drop(['Date', 'stations', 'observation'], axis=1, inplace=True)
ItemNum=18
#训练样本features集合
X_Train=[]
#训练样本目标PM2.5集合
Y_Train=[]
for i in range(int(len(train_data)/ItemNum)):
observation_data = train_data[i*ItemNum:(i+1)*ItemNum] #一天的观测数据
for j in range(15):
x = observation_data.iloc[:, j:j + 9]
y = int(observation_data.iloc[9,j+9])
# 将样本分别存入X_Train、Y_Train中
X_Train.append(x)
Y_Train.append(y)
# print(X_Train)
# print(Y_Train)
数据可视化
绘制散点图,预测各特征与 PM2.5 的关系
'''绘制散点图'''
x_AMB=[]
x_CH4=[]
x_CO=[]
x_NMHC=[]
# x_NO=[]
# x_NO2=[]
# x_NOX=[]
# x_O3=[]
# x_PM10=[]
# x_PM2Dot5=[]
# x_RAINFALL=[]
# x_RH=[]
# x_SO2=[]
# x_THC=[]
# x_WD_HR=[]
# x_WIND_DIREC=[]
# x_WIND_SPEED=[]
# x_WS_HR=[]
#
y=[]
#
# for i in range(len(Y_Train)):
# y.append(Y_Train[i])
# x=X_Train[i]
# # print(type(x.iloc[0,0]))
# # 求各测项的平均值
# x_WIND_SPEED_sum = 0
# x_WS_HR_sum = 0
# for j in range(9):
# x_WIND_SPEED_sum = x_WIND_SPEED_sum + float(x.iloc[0, j])
# x_WS_HR_sum = x_WS_HR_sum + float(x.iloc[1, j])
# x_WIND_SPEED.append(x_WIND_SPEED_sum / 9)
# x_WS_HR.append(x_WS_HR_sum / 9)
# plt.figure(figsize=(10, 6))
# plt.subplot(1, 2, 1)
# plt.title('WIND_SPEED')
# plt.scatter(x_WIND_SPEED, y)
# plt.subplot(1, 2, 2)
# plt.title('WS_HR')
# plt.scatter(x_WS_HR, y)
# plt.show()
# x_SO2_sum = 0
# x_THC_sum = 0
# x_WD_HR_sum = 0
# x_WIND_DIREC_sum = 0
# for j in range(9):
# x_SO2_sum = x_SO2_sum + float(x.iloc[0, j])
# x_THC_sum = x_THC_sum + float(x.iloc[1, j])
# x_WD_HR_sum = x_WD_HR_sum + float(x.iloc[2, j])
# x_WIND_DIREC_sum = x_WIND_DIREC_sum + float(x.iloc[3, j])
# x_SO2.append(x_SO2_sum / 9)
# x_THC.append(x_THC_sum / 9)
# x_WD_HR.append(x_WD_HR_sum / 9)
# x_WIND_DIREC.append(x_WIND_DIREC_sum / 9)
# plt.figure(figsize=(10, 6))
# plt.subplot(2, 2, 1)
# plt.title('SO2')
# plt.scatter(x_SO2, y)
# plt.subplot(2, 2, 2)
# plt.title('THC')
# plt.scatter(x_THC, y)
# plt.subplot(2, 2, 3)
# plt.title('WD_HR')
# plt.scatter(x_WD_HR, y)
# plt.subplot(2, 2, 4)
# plt.title('WIND_DIREC')
# plt.scatter(x_WIND_DIREC, y)
# plt.show()
# x_PM10_sum = 0
# x_PM2Dot5_sum = 0
# x_RAINFALL_sum = 0
# x_RH_sum = 0
# for j in range(9):
# x_PM10_sum = x_PM10_sum + float(x.iloc[0, j])
# x_PM2Dot5_sum = x_PM2Dot5_sum + float(x.iloc[1, j])
# x_RAINFALL_sum = x_RAINFALL_sum + float(x.iloc[2, j])
# x_RH_sum = x_RH_sum + float(x.iloc[3, j])
# x_PM10.append(x_PM10_sum / 9)
# x_PM2Dot5.append(x_PM2Dot5_sum / 9)
# x_RAINFALL.append(x_RAINFALL_sum / 9)
# x_RH.append(x_RH_sum / 9)
# plt.figure(figsize=(10, 6))
# plt.subplot(2, 2, 1)
# plt.title('PM10')
# plt.scatter(x_PM10, y)
# plt.subplot(2, 2, 2)
# plt.title('PM2.5')
# plt.scatter(x_PM2Dot5, y)
# plt.subplot(2, 2, 3)
# plt.title('RAINFALL')
# plt.scatter(x_RAINFALL, y)
# plt.subplot(2, 2, 4)
# plt.title('RH')
# plt.scatter(x_RH, y)
# plt.show()
x_AMB_sum=0
x_CH4_sum=0
x_CO_sum=0
x_NMHC_sum=0
for j in range(9):
x_AMB_sum = x_AMB_sum + float(x.iloc[0,j])
x_CH4_sum = x_CH4_sum + float(x.iloc[1, j])
x_CO_sum = x_CO_sum + float(x.iloc[2, j])
x_NMHC_sum = x_NMHC_sum + float(x.iloc[3, j])
x_AMB.append(x_AMB_sum / 9)
x_CH4.append(x_CH4_sum / 9)
x_CO.append(x_CO_sum / 9)
x_NMHC.append(x_NMHC_sum / 9)
plt.figure(figsize=(10, 6))
plt.subplot(2, 2, 1)
plt.title('AMB')
plt.scatter(x_AMB, y)
plt.subplot(2, 2, 2)
plt.title('CH4')
plt.scatter(x_CH4, y)
plt.subplot(2, 2, 3)
plt.title('CO')
plt.scatter(x_CO, y)
plt.subplot(2, 2, 4)
plt.title('NMHC')
plt.scatter(x_NMHC, y)
plt.show()
选择最具代表性的特征:PM10、PM2.5、SO2
模型建立
建立线性回归模型
定义损失函数 (Gradient Descent)
 采用小批量梯度下降算法,并且设定批量样本大小为50,即每次随机在训练样本中选取50个用来更新参数
采用小批量梯度下降算法,并且设定批量样本大小为50,即每次随机在训练样本中选取50个用来更新参数
设定学习率learning rate分别为0.000000001、0.0000001、0.000001时,比较不同的learning rate对损失函数收敛速度的影响
'''
利用 Linear Regression 线性回归预测 PM2.5
该方法参考黑桃大哥的优秀作业-|vv|-
'''
# 导入必要的包 numpy、pandas以及scikit-learn归一化预处理
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
# 指定相对路径
path = "./Dataset/"
# 利用 pands 进行读取文件操作
train = pd.read_csv(path + 'train.csv', engine='python', encoding='utf-8')
test = pd.read_csv(path + 'test.csv', engine='python', encoding='gbk')
train = train[train['observation'] == 'PM2.5']
# print(train)
test = test[test['AMB_TEMP'] == 'PM2.5']
# 删除无关特征
train = train.drop(['Date', 'stations', 'observation'], axis=1)
test_x = test.iloc[:, 2:]
train_x = []
train_y = []
for i in range(15):
x = train.iloc[:, i:i + 9]
# notice if we don't set columns name, it will have different columns name in each iteration
x.columns = np.array(range(9))
y = train.iloc[:, i + 9]
y.columns = np.array(range(1))
train_x.append(x)
train_y.append(y)
# review "Python for Data Analysis" concat操作
# train_x and train_y are the type of Dataframe
# 取出 PM2.5 的数据,训练集中一共有 240 天,每天取出 15 组 含有 9 个特征 和 1 个标签的数据,共有 240*15*9个数据
train_x = pd.concat(train_x) # (3600, 9) Dataframe类型
train_y = pd.concat(train_y)
# 将str数据类型转换为 numpy的 ndarray 类型
train_y = np.array(train_y, float)
test_x = np.array(test_x, float)
# print(train_x.shape, train_y.shape)
# 进行标准缩放,即数据归一化
ss = StandardScaler()
# 进行数据拟合
ss.fit(train_x)
# 进行数据转换
train_x = ss.transform(train_x)
ss.fit(test_x)
test_x = ss.transform(test_x)
# 定义评估函数
# 计算均方误差(Mean Squared Error,MSE)
# r^2 用于度量因变量的变异中 可以由自变量解释部分所占的比例 取值一般为 0~1
def r2_score(y_true, y_predict):
# 计算y_true和y_predict之间的MSE
MSE = np.sum((y_true - y_predict) ** 2) / len(y_true)
# 计算y_true和y_predict之间的R Square
return 1 - MSE / np.var(y_true)
# 线性回归
class LinearRegression:
def __init__(self):
# 初始化 Linear Regression 模型
self.coef_ = None
self.intercept_ = None
self._theta = None
def fit_normal(self, X_train, y_train):
# 根据训练数据集X_train, y_train训练Linear Regression模型
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
# 对训练数据集添加 bias
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
'''
:param X_train: 训练集
:param y_train: label
:param eta: 学习率
:param n_iters: 迭代次数
:return: theta 模型参数
'''
# 根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
# 定义损失函数
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')
# 对损失函数求导
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
'''
:param X_b: 输入特征向量
:param y: lebel
:param initial_theta: 初始参数
:param eta: 步长
:param n_iters: 迭代次数
:param epsilon: 容忍度
:return:theta:模型参数
'''
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1]) # 初始化theta
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self, X_predict):
# 给定待预测数据集X_predict,返回表示X_predict的结果向量
assert self.intercept_ is not None and self.coef_ is not None, \
"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_), \
"the feature number of X_predict must be equal to X_train"
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
# 根据测试数据集 X_test 和 y_test 确定当前模型的准确度
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return
# 模型训练
LR = LinearRegression().fit_gd(train_x, train_y)
# 评分
LR.score(train_x, train_y)
# 预测
result = LR.predict(test_x)
# 结果保存
sampleSubmission = pd.read_csv(path + 'sampleSubmission.csv', engine='python', encoding='gbk')
sampleSubmission['value'] = result
sampleSubmission.to_csv(path + 'result.csv')