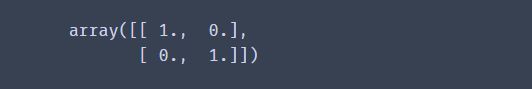Python 矩阵基本运算【numpy】
文章目录
-
-
- 一、实验说明
- 二、Python 矩阵基本运算
-
-
- 1. python矩阵操作
- 2. python矩阵乘法
- 3. python矩阵转置
- 4. python求方阵的迹
- 5. python方阵的行列式计算方法
- 6. python求逆矩阵/伴随矩阵
- 7. python解多元一次方程
-
-
一、实验说明
实验环境
Anaconda + python3.6 + jupyter
二、Python 矩阵基本运算
引入 numpy 库
import numpy as np
1. python矩阵操作
① 使用 mat 函数创建一个 2X3矩阵
a = np.mat([[1, 2, 3], [4, 5, 6]])
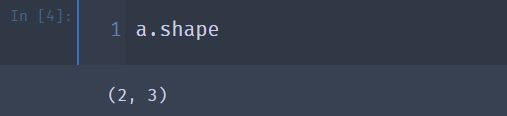
② 使用 shape 可以获取矩阵的大小
a.shape
③ 进行行列转换
a.T
④ 使用二维数组代替矩阵来进行矩阵运算
b = np.array([[1, 2, 3], [4, 5, 6]])
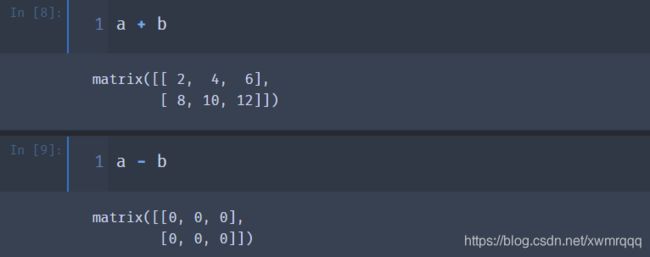
⑤ 加减法
a + b
a - b
2. python矩阵乘法
① 使用二维数组创建两个矩阵A和B
A = np.array([[1, 2, 3], [4, 5, 6]])
B = A.T
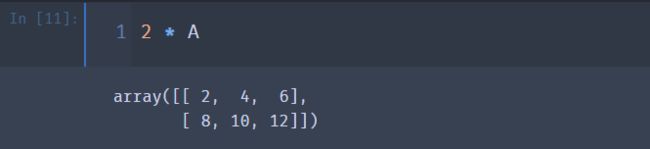
② 一个矩阵的数乘,其实就是矩阵的每一个元素乘以该数
2 * A
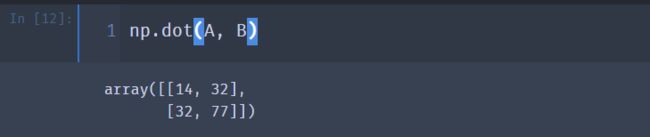
③ dot 函数用于矩阵乘法,对于二维数组,它计算的是矩阵乘积,对于一维数组,它计算的是内积
np.dot(A, B)
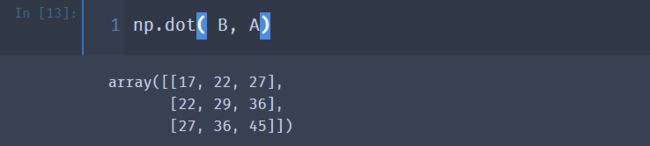
np.dot( B, A)
注意交换矩阵的前后位置会导致不同的结果
④ 再创建一个二维数组
C = np.array([[1, 2], [1, 3]])
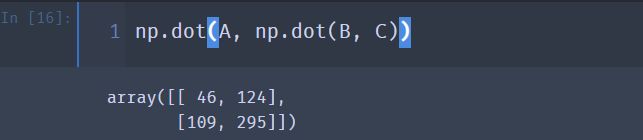
⑤ 验证矩阵乘法的结合性: ( A B ) C = A ( B C ) (AB)C = A(BC) (AB)C=A(BC)
np.dot(np.dot(A, B), C)
np.dot(A, np.dot(B, C))
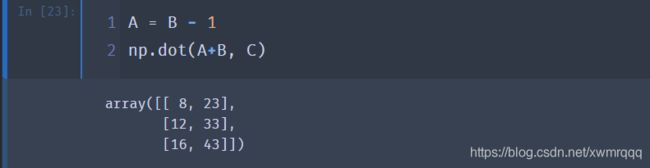
⑥ 验证矩阵加法的分配性: ( A + B ) C = A C + B C (A+B)C = AC + BC (A+B)C=AC+BC
A = B - 1
np.dot(A+B, C)
np.dot(A, C) + np.dot(B, C)
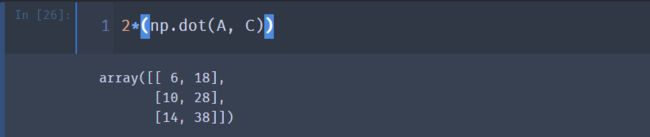
⑦ 数乘的结合性
2*(np.dot(A, C))
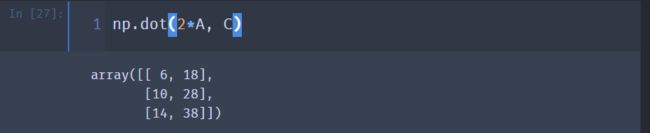
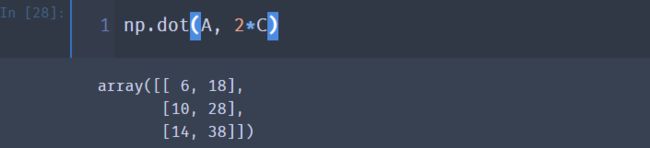
np.dot(2*A, C)
np.dot(A, 2*C)
⑧ 使用 eye 创建一个单位矩阵
D = np.eye(2)
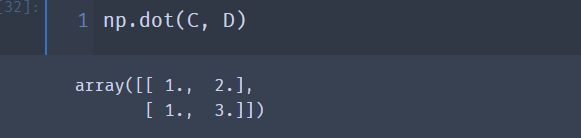
⑨ 一个矩阵乘以一个单位矩阵,还是它本身
np.dot(C, D)
3. python矩阵转置
矩阵的转置就是将矩阵的行变为列,将列变为行
① 第一个性质矩阵转置的转置就是它本身: ( A ′ ) ′ = A (A^{'})^{'} = A (A′)′=A
A = np.array([[1, 2, 3], [4, 5, 6]])
A.T.T
② 创建两个尺寸相同的矩阵
B = A.T
C = B - 1
③ 验证矩阵转置的第二个性质: ( A ± B ) ′ = A ′ ± B ′ (A \pm B)^{'} = A^{'} \pm B^{'} (A±B)′=A′±B′
(B + C).T
B.T + C.T
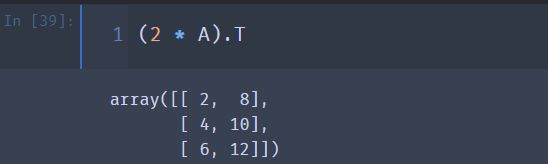
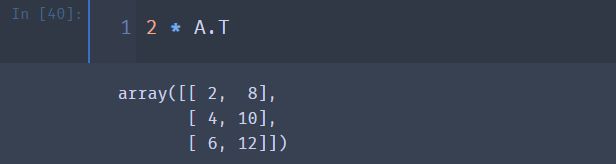
④ 验证矩阵转置的第三个性质: ( K A ) ′ = K A ′ (KA)^{'} = KA^{'} (KA)′=KA′
(2 * A).T
2 * A.T
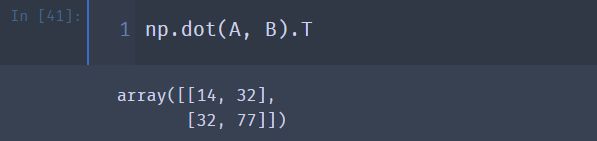
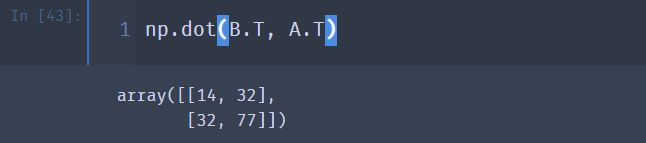
⑤ 验证矩阵转置的第四个性质: ( A × B ) ′ = B ′ × A ′ (A \times B)^{'} = B^{'} \times A^{'} (A×B)′=B′×A′
np.dot(A, B).T
np.dot(B.T, A.T)
4. python求方阵的迹
方阵的迹就是主对角元素之和
① 创建一个方阵(方阵也就是行数等于列数的矩阵)
E = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
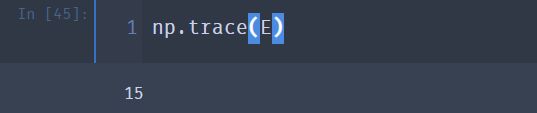
② 用 trace 计算方阵的迹
np.trace(E)
③ 再创建一个方阵F
F = E - 2
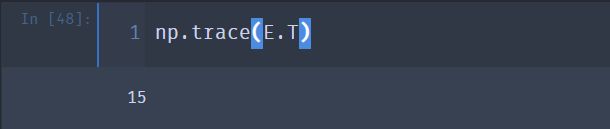
④ 验证一下方阵的迹等于方阵的转置的迹
np.trace(E)
np.trace(E.T)
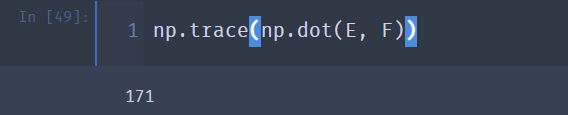
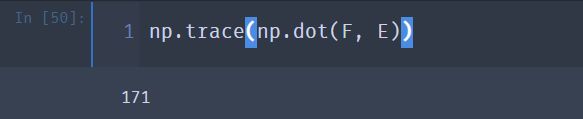
⑤ 验证一下方阵的乘积的迹
np.trace(np.dot(E, F))
np.trace(np.dot(F, E))
⑥ 验证一下方阵的和的迹等于方阵的迹的和
np.trace(E + F)
np.trace(E) + np.trace(F)
5. python方阵的行列式计算方法
① 创建两个方阵
E = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
F = np.array([[1, 2], [1, 3]])
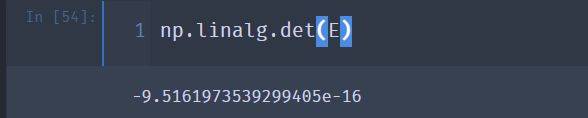
② 使用 linalg.det 方法求得方阵E和方阵F的行列式
np.linalg.det(E)
np.linalg.det(F)
6. python求逆矩阵/伴随矩阵
逆矩阵的定义:
设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E。 则我们称B是A的逆矩阵,而A则被称为可逆矩阵。当矩阵A的行列式|A|不等于0时才存在可逆矩阵。
伴随矩阵的定义:
设A为n节方阵,则由A的行列式|A|中各个元素的代数余子式 A i j A_{ij} Aij所构成的如下矩阵
A ∗ = [ A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋱ ⋮ A 1 n A 2 n ⋯ A n n ] A^* = \begin{bmatrix} A_{11} & A_{21} & \cdots & A_{n1}\\ A_{12} & A_{22} & \cdots & A_{n2}\\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{bmatrix} A∗=⎣⎢⎢⎢⎡A11A12⋮A1nA21A22⋮A2n⋯⋯⋱⋯An1An2⋮Ann⎦⎥⎥⎥⎤
称为矩阵A的伴随矩阵,或简称 “伴随阵”
① 创建一个方阵
A = np.array([[1, -2, 1], [0, 2, -1], [1, 1, -2]])
② 使用 linalg.det求得方阵的行列式
A_abs = np.linalg.det(A)
③ 使用 linalg.inv 求得方阵A的逆矩阵
B = np.linalg.inv(A)
④ 利用公式求伴随矩阵: A ∗ = ∣ A ∣ A − 1 A^* = |A|A^{-1} A∗=∣A∣A−1
A_bansui = B * A_abs
7. python解多元一次方程
使用python的numpy包中的 linalg.solve() 方法解多元一次方程
要求解的方程如下:
x + 2 y + z = 7 2 x − y + 3 z = 7 3 x + y + 2 z = 18 x + 2y + z =7 \\ 2x - y +3z = 7 \\ 3x + y + 2z = 18 x+2y+z=72x−y+3z=73x+y+2z=18
① 将未知数的系数写下来,排列成一个矩阵a
a = [[1, 2, 1], [2, -1, 3], [3, 1, 2]]
a = np.array(a)
② 常数项构成一个一维数组(向量)
b = [7, 7, 18]
b = np.array(b)
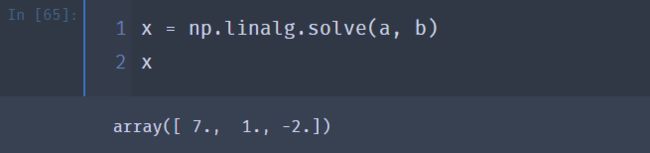
③ 使用 linalg.solve 方法解方程,参数a指的是系数矩阵,参数b指的是常数项矩阵
x = np.linalg.solve(a, b)
④ 使用点乘的方法可以验证一下,系数乘以未知数可以得到常数项
np.dot(a, x)