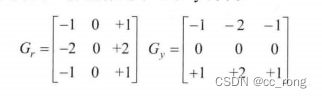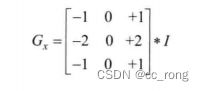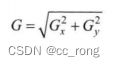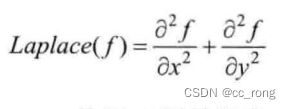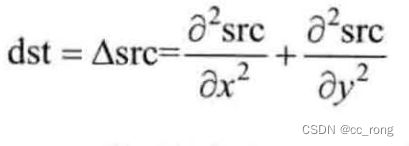《opencv学习笔记》-- 边缘检测和canny算子、sobel算子、LapIacian 算子、scharr滤波器
目录
边缘检测
canny算子
sobel算子
LapIacian 算子 (拉普拉斯)
scharr滤波器
边缘检测
边缘检测步骤:
1、滤波:
边缘检测的算法主要是基于图像强度的一阶和二阶导数,但导数通常对噪声很敏感,因此必须采用滤波器来改善与噪声有关的边缘检测器的性能。常见的滤波方法主要有高斯滤波,即采用离散化的高斯函数产生一组归一化的高斯核,然后基于高斯核函数对图像灰度矩阵的每一点进行加权求和。
2、增强:
增强边缘的基础是确定图像各点邻域强度的变化值。增强算法可以将图像灰度点邻域强度值有显著变化的点凸显出来。通过计算梯度幅值来确定。梯度相关算法:膨胀、腐蚀、开运算、闭运算、形态学梯度、顶帽(礼帽)、黑帽。
3、检测:
经过增强的图像,往往邻域中有很多点的梯度值比较大,而在特定的应用中,这些点并不是我们要找的边缘点,所以应该采用某种方法来对这些点进行取舍。实际工程中,常用的方法是通过阈值化方法来检测。
canny算子
canny算子的目标是:找到一个最优的边缘检测算法。
最优的边缘检测评价标准:
1.低错误率: 标识出尽可能多的实际边缘,同时尽可能的减少噪声产生的误报。
2.高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。
3.最小响应: 图像中的边缘只能标识一次,并且可能存在的图像噪声不应标识为边缘。
canny边缘检测的步骤:
1.消除噪声。一般情况下,使用高斯平滑滤波器卷积降噪。
如下显示了一个 size = 5 的高斯内核示例:
2.计算梯度幅值和方向。 按照Sobel滤波器的步骤。
i、运用一对卷积阵列 (分别作用于 x 和 y 方向):
ii、使用下列公式计算梯度幅值和方向:
梯度方向近似到四个可能角度之一(一般为0°, 45°, 90°, 135°)
3.非极大值抑制。 这一步排除非边缘像素, 仅仅保留了一些细线条(候选边缘)。
4.滞后阈值。Canny 使用了滞后阈值,滞后阈值需要两个阈值(高阈值和低阈值):
i.如果某一像素位置的幅值超过高阈值, 该像素被保留为边缘像素。
ii.如果某一像素位置的幅值小于低阈值, 该像素被排除。
iii.如果某一像素位置的幅值在两个阈值之间,该像素仅仅在连接到一个高于高阈值的
像素时被保留。
void canny(InputArray image, OutputArray edges, double threshold1, double threshold2, int apertureSize = 3, bool L2gradient = false )参数1,InputArray类型的image,输入图像,填Mat类的对象,且需为单通道8位图像。
参数2,OutputArray类型的edges,输出的边缘图,需和源图像有一样的尺寸和类型。
参数3,double类型的threshold1,第一个滞后性阈值。
参数4,double类型的threshold2,第二个滞后性阈值。
参数5,int类型的apertureSize,表示应用Sobel算子的孔径大小,其有默认值3。
参数6,bool类型的L2gradient,一个计算图像梯度幅值的标识,有默认值false。
注意:
threshold1和threshold2两者中的较小者用于边缘连接,而较大者用来控制强边缘的
初始段,推荐的高低阈值比在2:1到3:1之间。
//高阶的canny用法,转成灰度图,降噪,用canny,
//最后将得到的边缘作为掩码,拷贝原图到效果图上,
//得到彩色的边缘图
sobel算子
主要用作边缘检测的离散微分算子。
Sobel算子结合了高斯平滑和微分求导,用来计算图像灰度函数的近似梯度。在图像的任何一点使用此算子,将会产生对应的梯度矢量或是其法矢量。
优点:方法简单、处理速度快,并且所得的边缘光滑、连续。
缺点:边缘较粗,由于处理时需作二值化处理,故得到的边缘与阈值的选取也有很大的关系
sobel算子的步骤:
1.分别在x和y两个方向求导。
i、水平变化: 将 I 与一个奇数大小的内核Gx进行卷积。比如,当内核大小为3时,
Gx的计算结果为:
ii、垂直变化: 将 I 与一个奇数大小的内核Gx进行卷积。比如,当内核大小为3时,
Gx的计算结果为:
2.在图像的每一点,结合以上两个结果求出近似梯度:
使用扩展的 Sobel 算子,来计算一阶、二阶、三阶或混合图像差分。
void Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize = 3, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT);参数1,InputArray 类型的src,为输入图像,填Mat类型即可。
参数2,OutputArray类型的dst,即目标图像,需要和源图片有一样的尺寸和类型。
参数3,int类型的ddepth,输出图像的深度,支持如下src.depth()和ddepth的组合:
若src.depth() = CV_8U, 取ddepth = -1/CV_16S/CV_32F/CV_64F
若src.depth() = CV_16U/CV_16S, 取ddepth = -1/CV_32F/CV_64F
若src.depth() = CV_32F, 取ddepth = -1/CV_32F/CV_64F
若src.depth() = CV_64F, 取ddepth = -1/CV_64F
参数4,int类型dx,x 方向上的差分阶数,1或者0。
参数5,int类型dy,y方向上的差分阶数,1或者0。
参数6,int类型ksize,有默认值3,表示Sobel核的大小;可取值1,3,5或7。
参数7,double类型的scale,计算导数值时可选的缩放因子,默认值是1,
表示默认情况下是没有应用缩放的。
参数8,double类型的delta,表示在结果存入目标图(第二个参数dst)之前可选的delta值,
有默认值0。
参数9, int类型的borderType,边界模式,默认值为BORDER_DEFAULT。
一般情况下,都是用ksize X ksize内核来计算导数的。
有一种特殊情况 ------ 当ksize为1时,往往会使用3 X 1或者1 X 3的内核。且这种情况下,并没有进行高斯平滑操作。
1.当内核大小为 3 时, Sobel内核可能产生比较明显的误差(Sobel算子只是求取了导数的近似值而已)。 为解决这一问题,OpenCV提供了Scharr 函数,但该函数仅作用于大小为3的内核。该函数的运算与Sobel函数一样快,但结果却更加精确,其内核是这样的:
2.Sobel算子结合了高斯平滑和分化,因此结果会具有更多的抗噪性。大多数情况下,使用sobel函数时,取【xorder = 1,yorder = 0,ksize = 3】来计算图像X方向的导数,【xorder = 0,yorder = 1,ksize = 3】来计算图像y方向的导数。
计算图像X方向的导数,取【xorder= 1,yorder = 0,ksize = 3】对应的内核:
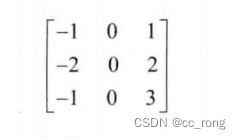
计算图像Y方向的导数,取【xorder= 0,yorder = 1,ksize = 3】对应的内核:
LapIacian 算子 (拉普拉斯)
LapIacian 算子是n维欧几里德空间中的一个二阶微分算子,定义为梯度grad()的散度div()。如果f是二阶可微的实函数,则f的拉普拉斯算子定义为:
1、f的拉普拉斯算子也是笛卡儿坐标系中的所有非混合二阶偏导数求和.
2 、作为一个二阶微分算子,拉普拉斯算子把C函数映射到C函数,对于k ≥ 2。表达式(1)(或(2))定义了一个算子Δ :C(R) → C(R),对于任何开集Ω,定义了一个算子 C(Ω) →C(Ω)。
Laplacian 算子的定义:
由于 Laplacian使用了图像梯度,Laplacian内部的代码是调用了 Sobel 算子的。
让一幅图像减去它的Laplacian算子可以增强对比度。
void Laplacian(InputArray src, OutputArray dst, int ddepth, int ksize = 1, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT );参数1,输入图像Mat类的对象, 且需为单通道8位图像。
参数2,输出的边缘图,需要和源图片有一样的尺寸和通道数。
参数3,int类型的ddept,目标图像的深度。
参数4,用于计算二阶导数的滤波器的孔径尺寸(高斯核大小),大小必须为正奇数,
且有默认值1。
参数5,计算拉普拉斯值的时候可选的比例因子,有默认值1。
参数6,表示在结果存入目标图(第二个参数dst)之前可选的delta值,有默认值0。
参数7,边界模式,默认值为BORDER_DEFAULT。这个参数可以在borderInterpolate()
中查看。
Laplacian()函数其实主要是利用sobel算子的运算。通过加上sobel算子运算出的图像x方向和y方向上的导数,来得到载入图像的拉普拉斯变换结果。其中,sobel算子(ksize>1)如下:
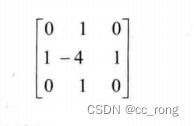
当ksize=1时,Laplacian()函数采用以下3 X 3的孔径:
scharr滤波器
主要是配合Sobel算子的运算而存在的。
使用Scharr滤波器运算符计算x或y方向的图像差分。
void Scharr( InputArray src, // 源图 OutputArray dst, // 目标图,需要和源图像一样的尺寸和类型 int ddepth, // 图像深度 int dx, // x方向上的差分阶数 int dy, // y方向上的差分阶数 double scale=1, // 缩放因子 double delta=0, // delta值 int borderType = BORDER_DEFAULT // 边界模式 )参数3,int类型的ddepth,输出图像的深度,支持如下src.depth()和ddepth的组合:
若src.depth() = CV_8U, 取ddepth = -1/CV_16S/CV_32F/CV_64F
若src.depth() = CV_16U/CV_16S, 取ddepth = -1/CV_32F/CV_64F
若src.depth() = CV_32F, 取ddepth = -1/CV_32F/CV_64F
若src.depth() = CV_64F, 取ddepth = -1/CV_64F
参数6,计算导数值时可选的缩放因子,默认值是1,表示默认情况下是没有应用缩放的。
Scharr(src, dst, ddepth, dx, dy, scale, delta, borderType); 等价
Sobel(src, dst, ddepth, dx, dy, CV_SCHARR, scale, delta, borderType);