Planning-Apollo速度决策规划

Apollo采用路径规划和速度规划解耦的方式，先进行路径规划，在得到的规划路径上再进行速度规划。利用ST Graph，将障碍物、限速等投影在ST图上，利用全局搜索方法DP算法得到决策，在利用最优化方法进行速度规划。

1. 算法原理

百度已经将算法原理发表在论文《Optimal Trajectory Generation for Autonomous Vehicles Under Centripetal Acceleration Constraints for In-lane Driving Scenarios》中。

1.1 优化模型离散方式

在处理最优化问题时，一般会转化成离散形式，将轨迹$s(t)$按照某参数离散，并计算离散点处的约束和$cost$。不同的离散方式会构建不同的优化模型。对于速度规划问题，一般可以按照等间距离散(Spatial Parameter Discretization)和等时间离散(Temporal Parameter Discretization)。

1.1.1 Spatial Parameter Discretization

使用纵向距离$s$作为离散采样参数，假设第一个采样点$s=0$，连续采样离散点之间等间隔$\Delta s$离散，那么优化问题的决策变量为每个离散点的$\dot{s},\ddot{s}$和相邻采样点之间的时间间隔$\Delta t$。

优点：

• 参考线或者规划路径的曲率$\kappa$是纵向距离$s$的函数，因此向心加速度约束是容易处理的；
• 地图限速等速度约束是和纵向距离$s$相关的，那么优化问题的$\dot{s}$约束容易计算；

缺点：

• 优化问题的目标函数难以建模。Apollo规划算法用来优化纵向冲击度最小，冲击度使用相邻两个离散点的差分计算，如果采用$\Delta s$离散会使决策变量之间有除法运算，形成非凸优化问题；
• 难以施加安全约束。障碍物一般投影在ST Graph中，会得到每个时刻下的安全行驶范围$(s_{min},s_{max})$，即可行驶区域$s_{free}(t)$是时间$t$的函数。

1.1.2 Temporal Parameter Discretization

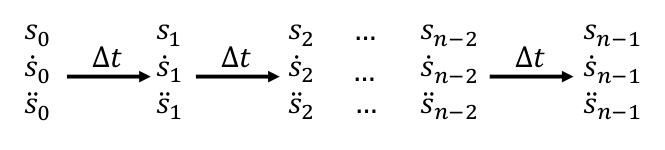
使用时间$t$作为离散采样参数，假设第一个采样点$t=0$，连续采样离散点之间等间隔$\Delta t$离散，那么优化问题的决策变量为每个离散点的$s,\dot{s},\ddot{s}$。

使用等时间间隔离散的方式，和使用等距离离散方式的优缺点恰好相反。

优点：

• 优化模型可以保持凸包性质，冲击度的计算仍然是线性形式；
• 障碍物的安全约束容易施加在优化模型中；

缺点：

• 由于曲率是$s$的函数，因此向心加速度约束难以处理；
• 速度约束难以处理；
• 最小任务完成时间的优化目标难以处理；

处理方法：

• 使用规划路径的最大曲率计算向心加速度限制；
• 将离散点处的位置$s$与DP得到纵向位置$s$的差作为目标函数的一部分，使用DP结果在采样时刻t处的s处对应的速度限值；
• 将离散采样点处的速度$\dot{s}$与目标速度(reference speed)的差作为目标函数的一部分。以保证完成任务花费的时间最少；

此外，Apollo还设计了非线性速度规划来处理以上问题。

1.2 优化问题建模

1.2.1 cost function

$$\begin{gathered} J=w_{\ddot{s}}\ast \sum _{i=0}^{n-1}{\ddot{s}}_i^2+w_{s^{(3)}}\ast \sum _{i=0}^{n-2}(s^{(3)}{)}_{i\to i+1}^2+w_{a_c}\ast \sum _{i=0}^{n-1}{\dot{s}}_i^2\ast \kappa (s_i) \\ +w_{s_{ref}}\ast \sum _{i=0}^{n-1}(s_i-s_{i,ref}{)}^2+w_{{\dot{s}}_{ref}}\ast \sum _{i=0}^{n-1}(\dot{s_i}-{\dot{s}}_{i,ref}{)}^2 \\ +w_{s_{task}}\ast (s_{n-1}-s_{task}{)}^2+w_{{\dot{s}}_{task}}\ast ({\dot{s}}_{n-1}-{\dot{s}}_{task}{)}^2+w_{{\ddot{s}}_{task}}\ast ({\ddot{s}}_{n-1}-{\ddot{s}}_{task}{)}^2\text{\hspace{1em}(1-1)} \end{gathered}$$

其中，
$$s_{i\to i+1}^{(3)}=\frac{{\ddot{s}}_{i+1}-{\ddot{s}}_i}{\Delta st}\text{\hspace{1em}(1-2)}$$

1.2.2 constraints

不等式约束：
$$\begin{gathered} s_i\in s_{free}(i\ast \Delta t) \\ {\dot{s}}_i\in [0,{\dot{s}}_{max}] \\ {\ddot{s}}_i\in [{\ddot{s}}_{min},{\ddot{s}}_{max}] \\ {s}_{i\to i+1}^{(3)}\in [s_{min}^{(3)},s_{max}^{(3)}] \\ {a}_{c_i}\in [-a_{c_{max}},a_{c_{max}}],a_{c_i}={\dot{s}}_i^2\ast \kappa (s_i)\text{\hspace{1em}(1-3)} \end{gathered}$$
等式约束：
$$\begin{array}{rl}{\ddot{s}}_{i+1}& ={\ddot{s}}_i+{\int }_0^{\Delta t}{s}_{i\to i+1}^{(3)}dt={\ddot{s}}_i+s_{i\to i+1}^{(3)}\times \Delta t\\ {\dot{s}}_{i+1}& ={\dot{s}}_i+{\int }_0^{\Delta t}{\ddot{s}}_{i\to i+1}dt={\dot{s}}_i+{\ddot{s}}_i\times \Delta t+\frac{1}{2}{s}_{i\to i+1}^{(3)}\times {\Delta t}^2\\ s_{i+1}& =s_i+{\int }_0^{\Delta t}{\dot{s}}_{i\to i+1}dt=s{l}_i+{\dot{s}}_i\times \Delta t+\frac{1}{2}{\ddot{s}}_i\times {\Delta t}^2+\frac{1}{6}{s}_{i\to i+1}^{(3)}\times {\Delta t}^3\end{array}\text{\hspace{1em}(1-4)}$$

2. ST Graph

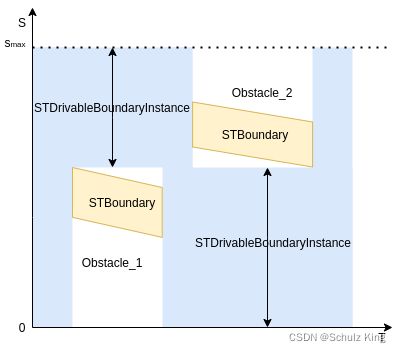
ST Graph即是以时间$t$为横轴，以纵向位移$s$为纵轴的直角坐标系，将PredictionObstacles和Speed limit等投影在坐标系上，计算出ADC在每个采样时间$t_{sample}$上的$s,\dot{s}$约束边界。class StGraphData的成员变量有st_boundaries_和st_drivable_boundary_，两者的区别是st_boundaries_是障碍物在ST图上的投影区域，是ADC的不可通行区域，如下图中的浅黄色区域。st_drivable_boundary_是ADC在ST图中的可通行区域，如下图中的浅蓝色区域。

在lanw_follow_config.pb.txt的默认配置中，会分别计算st_boundaries_和st_drivable_boundary_，但是具体使用哪个boundary计算ADC的可行驶区域会通过FLAGS_use_st_drivable_boundary进行控制。例如在DP过程中计算障碍物的cost：

// dp_st_cost.cc
double DpStCost::GetObstacleCost(const StGraphPoint& st_graph_point) {
  const double s = st_graph_point.point().s();
  const double t = st_graph_point.point().t();

  double cost = 0.0;
  // default: FLAGS_use_st_drivable_boundary = false
  // d判断StGraphPoint是否在可行驶范围内
  if (FLAGS_use_st_drivable_boundary) {
    // TODO(Jiancheng): move to configs
    static constexpr double boundary_resolution = 0.1;
    int index = static_cast(t / boundary_resolution);
    const double lower_bound =
        st_drivable_boundary_.st_boundary(index).s_lower();
    const double upper_bound =
        st_drivable_boundary_.st_boundary(index).s_upper();

    if (s > upper_bound || s < lower_bound) {
      return kInf;
    }
  }
  // 遍历所有的obstacle的cost求和
  for (const auto* obstacle : obstacles_) {
    // Not applying obstacle approaching cost to virtual obstacle like created
    // stop fences
    if (obstacle->IsVirtual()) {
      continue;
    }

    // Stop obstacles are assumed to have a safety margin when mapping them out,
    // so repelling force in dp st is not needed as it is designed to have adc
    // stop right at the stop distance we design in prior mapping process
    if (obstacle->LongitudinalDecision().has_stop()) {
      continue;
    }

    auto boundary = obstacle->path_st_boundary();

    if (boundary.min_s() > FLAGS_speed_lon_decision_horizon) {
      continue;
    }
    if (t < boundary.min_t() || t > boundary.max_t()) {
      continue;
    }
    // 碰撞的cost为无穷大
    if (boundary.IsPointInBoundary(st_graph_point.point())) {
      return kInf;
    }
    double s_upper = 0.0;
    double s_lower = 0.0;
    // 计算不碰撞时的cost
    int boundary_index = boundary_map_[boundary.id()];
    // 尚未计算obstacle在时间t处的上下边界，此时调用GetBoundarySRange计算边界，并储存起来，下次就不用计算了
    if (boundary_cost_[boundary_index][st_graph_point.index_t()].first < 0.0) {
      boundary.GetBoundarySRange(t, &s_upper, &s_lower);
      boundary_cost_[boundary_index][st_graph_point.index_t()] =
          std::make_pair(s_upper, s_lower);
    } else {
      s_upper = boundary_cost_[boundary_index][st_graph_point.index_t()].first;
      s_lower = boundary_cost_[boundary_index][st_graph_point.index_t()].second;
    }
    if (s < s_lower) {
      // proto default: safe_distance = 20.0
      const double follow_distance_s = config_.safe_distance();
      if (s + follow_distance_s < s_lower) {
        // 距离障碍物较远，cost = 0
        continue;
      } else {
        // 距离障碍物较近，越近cost越大
        auto s_diff = follow_distance_s - s_lower + s;
        // default: obstacle_weight: 1.0, proto default: default_obstacle_cost = 1e10
        cost += config_.obstacle_weight() * config_.default_obstacle_cost() *
                s_diff * s_diff;
      }
    } else if (s > s_upper) {
      const double overtake_distance_s =
          StGapEstimator::EstimateSafeOvertakingGap();  // default: 20.0m
      if (s > s_upper + overtake_distance_s) {  // or calculated from velocity
        // 越过obstacle较远，cost = 0
        continue;
      } else {
        // 距离障碍物越近cost越大
        auto s_diff = overtake_distance_s + s_upper - s;
        cost += config_.obstacle_weight() * config_.default_obstacle_cost() *
                s_diff * s_diff;
      }
    }
  }
  return cost * unit_t_;
}

以下为StGraphData、STBoundary、STDrivableBoundary的定义：

// st_graph_data.h
class StGraphData {
 public:
  StGraphData() = default;
  // ...
 private:
  // ...
  std::vector st_boundaries_;
  STDrivableBoundary st_drivable_boundary_;
};

class STBoundary : public common::math::Polygon2d {
 public:
  enum class BoundaryType {
    UNKNOWN,
    STOP,
    FOLLOW,
    YIELD,
    OVERTAKE,
    KEEP_CLEAR,
  };
  // ...
 private:
  BoundaryType boundary_type_ = BoundaryType::UNKNOWN;  // boundary type,可以看做是纵向决策

  std::vector upper_points_;
  std::vector lower_points_;

  std::string id_;  // obstacle ID
  double characteristic_length_ = 1.0;  // ??? 
  double min_s_ = std::numeric_limits::max();
  double max_s_ = std::numeric_limits::lowest();
  double min_t_ = std::numeric_limits::max();
  double max_t_ = std::numeric_limits::lowest();

  STPoint bottom_left_point_;
  STPoint bottom_right_point_;
  STPoint upper_left_point_;
  STPoint upper_right_point_;
  // ...
};

syntax = "proto2";

package apollo.planning;

message STDrivableBoundaryInstance {
  optional double t = 1;
  optional double s_lower = 2;
  optional double s_upper = 3;
  optional double v_obs_lower = 4;
  optional double v_obs_upper = 5;
}

message STDrivableBoundary {
  repeated STDrivableBoundaryInstance st_boundary = 1;
}

3. 代码实现

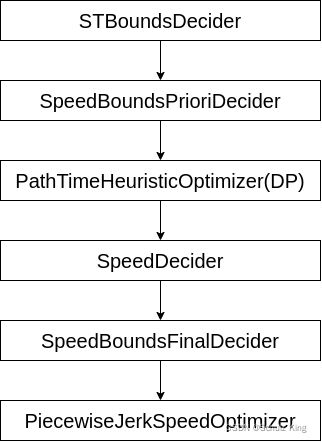
在Apollo中速度决策规划的实现流程如下：

3.1 STBoundsDecider

STBoundsDecider是来计算ST Graph中st_drivable_boundary_。由三个模块的计算组成：

• 车辆动力学约束计算得到的$s_{min},s_{max}$；
• 由参考速度行驶得到的$s_{min},s_{max}$；
• 由障碍物计算得到的可行驶区域$s_{min},s_{max}$；

3.1.1 车辆动力学约束

其计算依据为车辆运动学公式：
$$s=s_0+v_{0}t+\frac{1}{2}a{t}^2\text{\hspace{1em}(3-1)}$$
以下为计算ADC动力学运动范围的代码实现：

// st_driving_limits.cc
// 根据adc的最大动力学边界计算s的范围
std::pair STDrivingLimits::GetVehicleDynamicsLimits(
    const double t) const {
  std::pair dynamic_limits;
  // Process lower bound: (constant deceleration)
  // 以最大减速度减速到0的时间
  double dec_time = lower_v0_ / max_dec_;
  if (t - lower_t0_ < dec_time) {
    dynamic_limits.first =
        lower_s0_ + (lower_v0_ - max_dec_ * (t - lower_t0_) + lower_v0_) *
                        (t - lower_t0_) * 0.5;
  } else {
    dynamic_limits.first = lower_s0_ + (lower_v0_ * dec_time) * 0.5;
  }

  // Process upper bound: (constant acceleration)
  // 以最大加速度加速到最大速度的时间
  double acc_time = (max_v_ - upper_v0_) / max_acc_;
  if (t - upper_t0_ < acc_time) {
    dynamic_limits.second =
        upper_s0_ + (upper_v0_ + max_acc_ * (t - upper_t0_) + upper_v0_) *
                        (t - upper_t0_) * 0.5;
  } else {
    dynamic_limits.second = upper_s0_ + (upper_v0_ + max_v_) * acc_time * 0.5 +
                            (t - upper_t0_ - acc_time) * max_v_;
  }

  return dynamic_limits;
}

3.1.2 参考速度的行驶范围约束

其计算依据为运动学公式：
$$s=s_0+v_{ref}t\text{\hspace{1em}(3-2)}$$

3.1.3 障碍物计算的行驶范围约束

计算出障碍物的STBoundary和相应的限速。

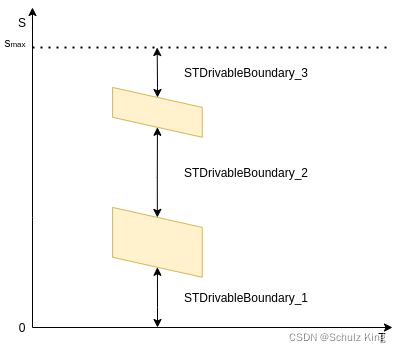
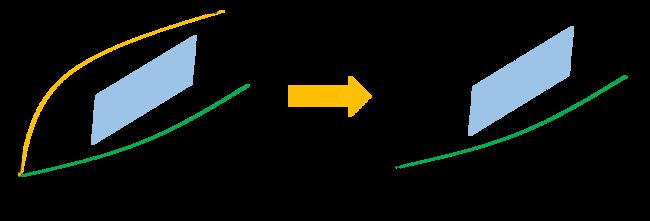
在这里存在的问题是由于没有决策信息，或者说决策信息不完整，对于障碍物形成的多个STDrivableBoundary应该选择哪一个。如下图所示，两个障碍物在ST Graph上会形成三个STDrivableBoundary。在STBoundsDecider中会根据下面三个条件来进行选择：

• STDrivableBoundary是否在车辆动力学约束范围附近；
• STDrivableBoundary是否包括按照参考速度行驶时的位移；
• STDrivableBoundary哪个的区域$(s_{max}-s_{min})$更大；

3.2 SpeedBoundsPrioriDecider

SpeedBoundsPrioriDecider对应的Decider或者说class是SpeedBoundsDecider，是计算每个障碍物的STBoundary得到ST Graph中的st_boundaries_和speed_limit_(SpeedLimit)。其中每个障碍物的STBoundary的计算其实是根据遍历规划时间内障碍物和规划路径的碰撞关系来计算的，并且会根据是否对障碍物做过纵向决策以及决策类型设置其STBoundary的characteristic_length。

speed_limit_(SpeedLimit)则是根据三个方面计算的：

• 地图限速；
• 向心加速度限制；
• 对于近距离nudge障碍物的减速避让；

限速值是上述三种限速的最小值。

3.3 PathTimeHeuristicOptimizer

PathTimeHeuristicOptimizer是速度规划的DP过程。速度规划需要在凸空间内求解，然而由于障碍物等原因会使求解空间变成非凸的，因此需要DP算法得到对不同障碍物的决策，从而得到一个凸空间。另一方面，最优化问题一般都仅有局部寻优能力，可能会收敛到某个局部最优解。为了保障优化问题的求解质量，使用全局“视野”的DP算法快速生成粗糙的初始解，并从该初始解的领域开展局部优化可以使最优化问题收敛到全局近似解。

3.4 SpeedDecider

SpeedDecider根据DP算法生成的速度曲线$s(t)$和障碍物的STBoundary的位置关系生成Ignore、Stop、Follow、Yield、Overtake的纵向决策。

• Ignore：
  • 障碍物的STBoundary在ST Graph的范围内；
  • 已经有纵向决策的障碍物；
  • 类型是禁停区的obstacle的STBoundary位于速度曲线的下方；
• Stop：
  • 前方是行人的停车决策；
  • 类型是禁停区的obstacle的STBoundary位于速度曲线的上方；
  • 在ADC前方低速行驶的堵塞道路的障碍物；
  • STBoundary和速度曲线相交的障碍物；
• Follow：
  • STBoundary位于速度曲线上方，且不需要Stop的障碍物；
• Yield：
  • STBoundary位于速度曲线上方，且不需要Stop和Follow的障碍物；
• Overtake：
  • STBoundary位于速度曲线下方的障碍物；

3.5 SpeedBoundsFinalDecider

SpeedBoundsFinalDecider对应的Decider同样是SpeedBoundsDecider，和SpeedBoundsPrioriDecider不同的是配置参数，从Apollo中的默认配置参数来看，SpeedBoundsFinalDecider会根据DP过程生成的决策结果和更小的boundary_buffer生成更加精确的STBoundary。

default_task_config: {
  task_type: SPEED_BOUNDS_PRIORI_DECIDER
  speed_bounds_decider_config {
    total_time: 7.0
    boundary_buffer: 0.25
    max_centric_acceleration_limit: 2.0
    point_extension: 0.0
    lowest_speed: 2.5
    static_obs_nudge_speed_ratio: 0.6
    dynamic_obs_nudge_speed_ratio: 0.8
  }
}
default_task_config: {
  task_type: SPEED_BOUNDS_FINAL_DECIDER
  speed_bounds_decider_config {
    total_time: 7.0
    boundary_buffer: 0.1
    max_centric_acceleration_limit: 2.0
    point_extension: 0.0
    lowest_speed: 2.5
    static_obs_nudge_speed_ratio: 0.6
    dynamic_obs_nudge_speed_ratio: 0.8
  }
}

3.6 PiecewiseJerkSpeedOptimizer

速度规划的优化求解即是按照上述的算法原理实现的。可以看到，在此会依据纵向决策结果生成纵向位移的约束边界，将每个时刻和cruise speed的误差作为优化目标的一部分，并且根据DP结果在每个时刻处位移的速度约束作为优化问题的速度约束边界，因此将每个时刻的位移和DP的位置之差作为了优化目标的一部分，但是这样只能实现速度的软约束。

  piecewise_jerk_problem.set_dx_ref(config.ref_v_weight(),
                                    reference_line_info_->GetCruiseSpeed());

  // Update STBoundary
  std::vector> s_bounds;
  for (int i = 0; i < num_of_knots; ++i) {
    double curr_t = i * delta_t;
    double s_lower_bound = 0.0;
    double s_upper_bound = total_length;
    for (const STBoundary* boundary : st_graph_data.st_boundaries()) {
      double s_lower = 0.0;
      double s_upper = 0.0;
      if (!boundary->GetUnblockSRange(curr_t, &s_upper, &s_lower)) {
        continue;
      }
      switch (boundary->boundary_type()) {
        case STBoundary::BoundaryType::STOP:
        case STBoundary::BoundaryType::YIELD:
          s_upper_bound = std::fmin(s_upper_bound, s_upper);
          break;
        case STBoundary::BoundaryType::FOLLOW:
          // TODO(Hongyi): unify follow buffer on decision side
          s_upper_bound = std::fmin(s_upper_bound, s_upper - 8.0);
          break;
        case STBoundary::BoundaryType::OVERTAKE:
          s_lower_bound = std::fmax(s_lower_bound, s_lower);
          break;
        default:
          break;
      }
    }
    if (s_lower_bound > s_upper_bound) {
      const std::string msg =
          "s_lower_bound larger than s_upper_bound on STGraph";
      AERROR << msg;
      speed_data->clear();
      return Status(ErrorCode::PLANNING_ERROR, msg);
    }
    s_bounds.emplace_back(s_lower_bound, s_upper_bound);
  }
  piecewise_jerk_problem.set_x_bounds(std::move(s_bounds));

  // Update SpeedBoundary and ref_s
  std::vector x_ref;
  std::vector penalty_dx;
  std::vector> s_dot_bounds;
  const SpeedLimit& speed_limit = st_graph_data.speed_limit();
  for (int i = 0; i < num_of_knots; ++i) {
    double curr_t = i * delta_t;
    // get path_s
    SpeedPoint sp;
    // DP过程计算的结果
    reference_speed_data.EvaluateByTime(curr_t, &sp);
    const double path_s = sp.s();
    x_ref.emplace_back(path_s);
    // get curvature
    PathPoint path_point = path_data.GetPathPointWithPathS(path_s);
    // default: kappa_penalty_weight = 2000.0
    // 对横向加速度进行约束
    // 用DP的结果查询t时刻的曲率(t时刻的曲率本是不可知的)，将非线性约束转换为线性约束
    penalty_dx.push_back(std::fabs(path_point.kappa()) *
                         config.kappa_penalty_weight());
    // get v_upper_bound
    const double v_lower_bound = 0.0;
    double v_upper_bound = FLAGS_planning_upper_speed_limit;
    v_upper_bound = speed_limit.GetSpeedLimitByS(path_s);
    s_dot_bounds.emplace_back(v_lower_bound, std::fmax(v_upper_bound, 0.0));
  }
  // default: ref_s_weight = 10.0
  piecewise_jerk_problem.set_x_ref(config.ref_s_weight(), std::move(x_ref));
  piecewise_jerk_problem.set_penalty_dx(penalty_dx);
  piecewise_jerk_problem.set_dx_bounds(std::move(s_dot_bounds));