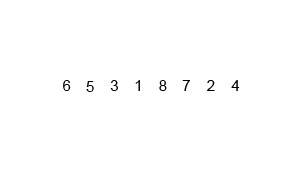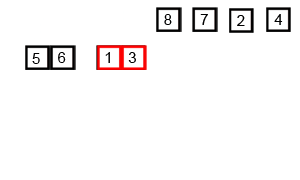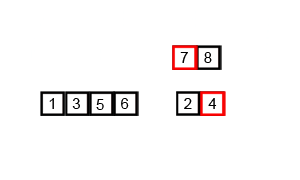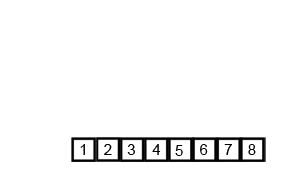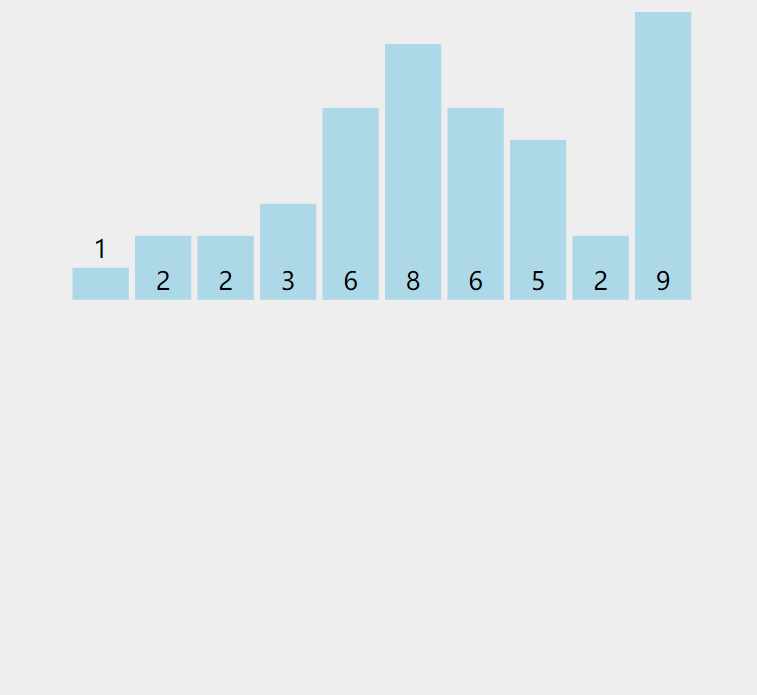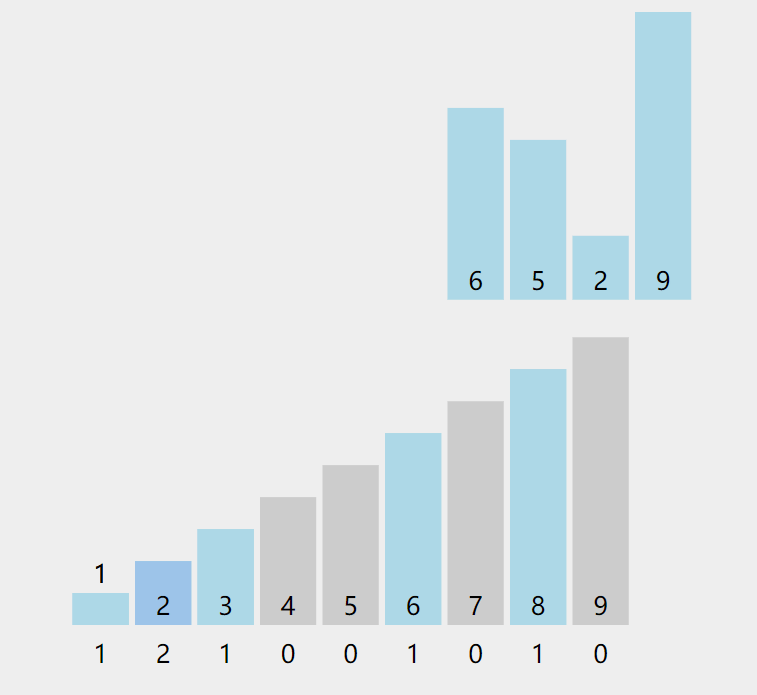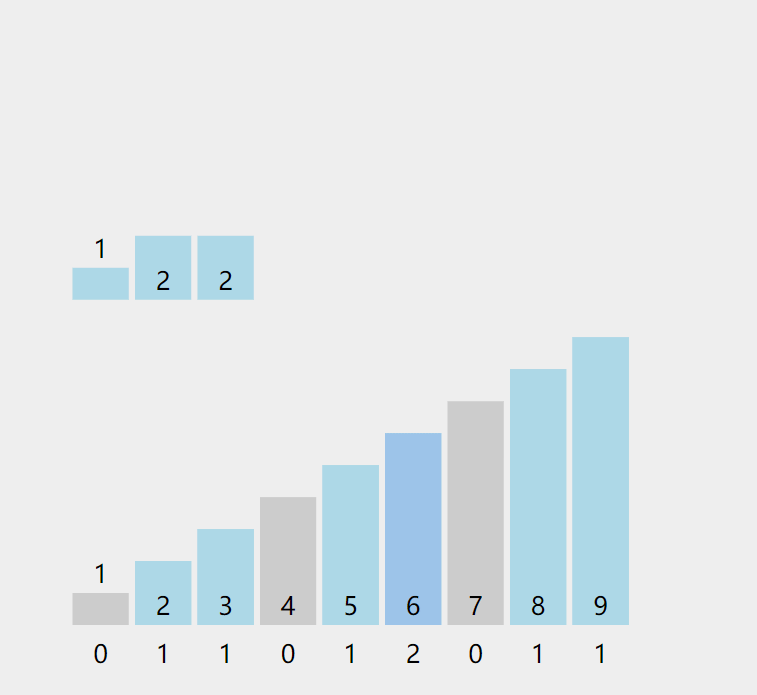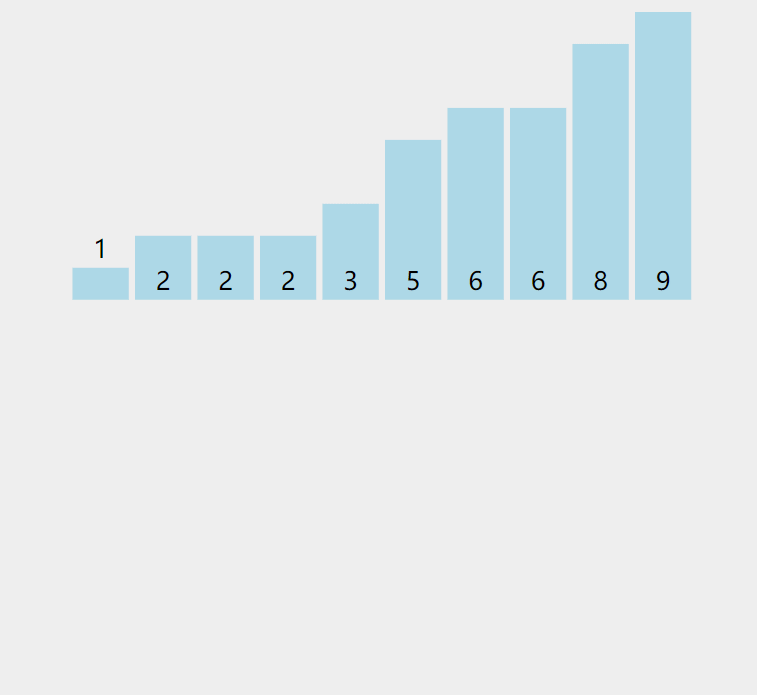八大排序总是忘?快来这里~
目录
插入排序
希尔排序
选择排序
冒泡排序
堆排序
快速排序(递归)
快速排序(迭代)
归并排序(递归)
归并排序(迭代)
计数排序
注意:本文所有排序默认升序
插入排序
思路:
- 首先从第一个元素开始可以被认为是已排好的元素
- 向后遍历,从第二个元素开始,每次从后向前扫描
- 遍历的元素若小于扫描到的元素,则交换,若没有,则将正在扫描的下一个元素正在遍历的元素交换
- 重复以上操作,直到遍历完成
代码如下:
public void insertSort(int[] array){
for(int i = 1; i < array.length; i++){
int key = array[i];
int j = i - 1;
for(; j >= 0; j--){
if(array[j] > key){
array[j + 1] = array[j];
}else{
break;
}
}
array[j + 1] = key;
}
}分析:
- 时间复杂度:O(N^2) -> 数组为逆序; O(N)->数组顺序
- 空间复杂度:O(1)
- 稳定性:稳定(稳定的可以修改为不稳定的,而不稳定的则不能修改为稳定的)
- 思考:适合用于元素集合趋于稳定的(效率更高)
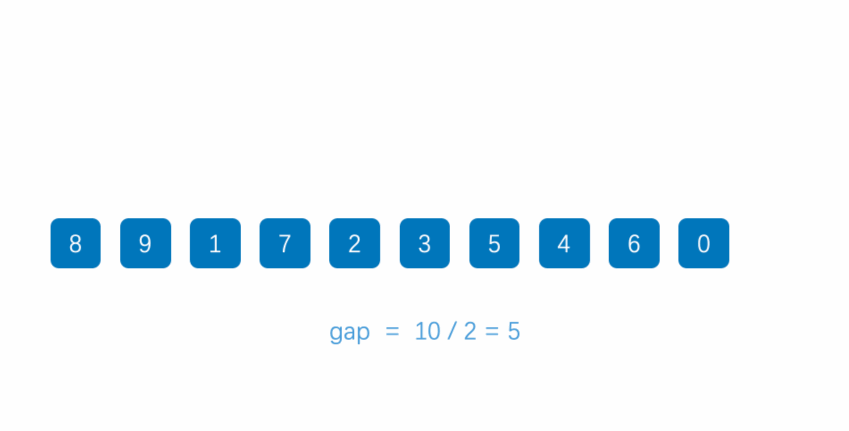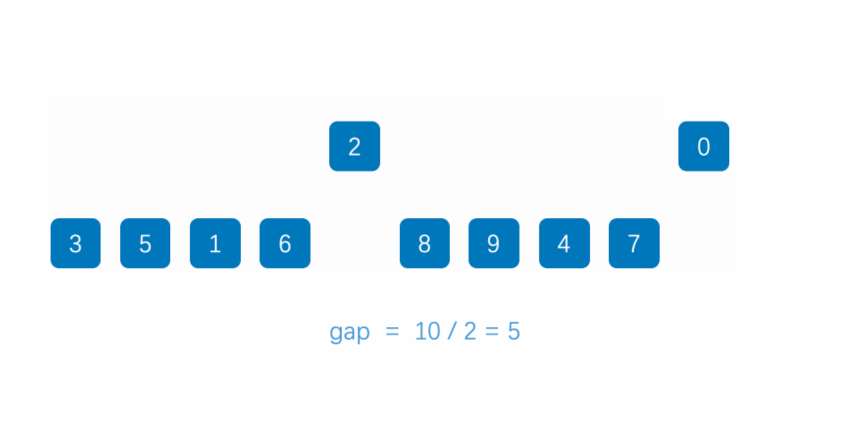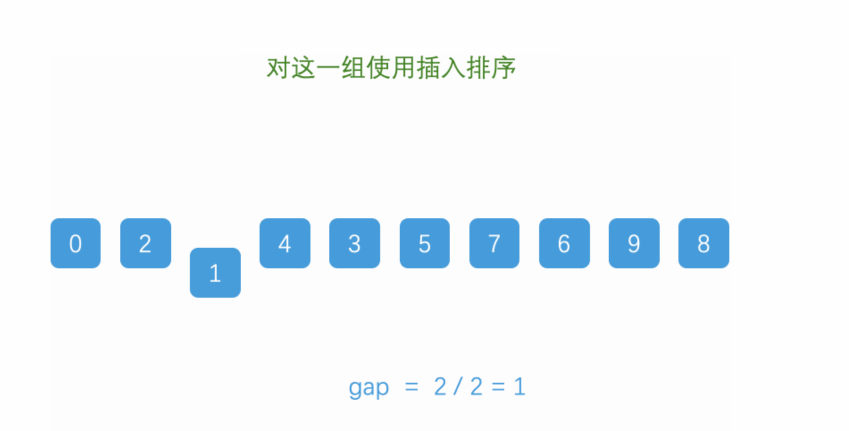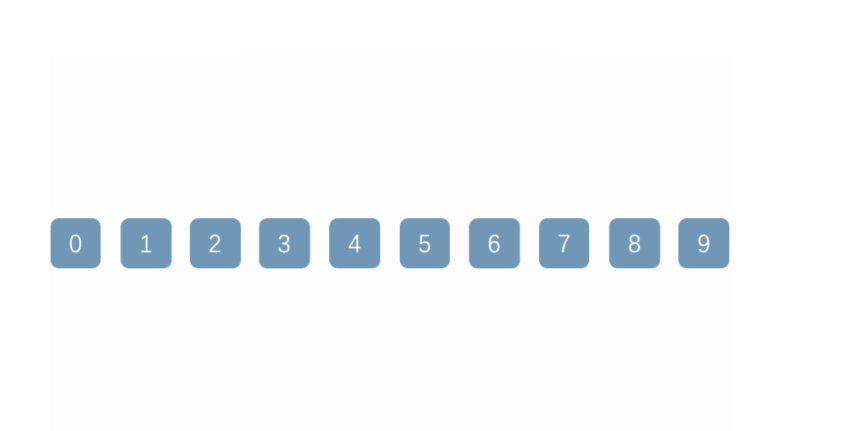
希尔排序
思路:
- 用一个数gap(一般为元素总数除2)将待排序元素分成若干个组,组距为gap
- 对每个组进行排序
- 缩小gap的值(一般除2)
- 继续重复以上操作
- 直到gap值为1时,再重复以上操作即可
- 本质是插入排序,但是会被分为若干组进行排序,逐渐趋向有序
代码如下:
public void shell3(int[] array, int gap){
for(int i = gap ; i < array.length; i++){
int key = array[i];
int j = i - gap;
for(; j >= 0; j -= gap){
if(array[j] > key){
array[j + gap] = array[j];
}else{
break;
}
}
array[j + gap] = key;
}
}
public void shellSort3(int[] array){
int gap = array.length;
while(gap > 1){
gap /= 2;
shell3(array, gap);
}
shell3(array, 1);
}分析:
- 时间复杂度:O(N^1.3 ~ N^1.4)
- 空间复杂度:O(1)
- 稳定性:不稳定
- 思考:是对插入排序的优化,更适合无序的元素
选择排序
思路:
- 从待排序的元素中遍历挑出一个最小值
- 存放在起始位置
- 再从这个起始位置向后遍历找出下一个最小值
- 存放在上一个起始位置的下一个位置
- 重复以上两步操作
- 直到全部排完
代码如下:
public void chooseSort(int[] array){
for(int i = 0; i < array.length; i++){
for(int j = i + 1; j < array.length; j++){
if(array[i] > array[j]){
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
}
}分析:
- 时间复杂度:O(N^2) 无论是有序还是无序,都是这么大
- 空间复杂度:O(1)
- 稳定性:不稳定
- 思考:效率不高,少用
冒泡排序
思路:
- 从起始位置开始,两两向后比较,若第一个大于第二个,则交换
- 用以上方法遍历(除了最后一个元素)完一遍后会将最大的元素排到最后
- 重复以上方法(已经排到后面的元素不用进行比较了)
- 直到没有要比较的元素后,停止
代码如下:
public void bubbleSort(int[] array){
for(int i = 0; i < array.length - 1; i++){
for(int j = 0; j < array.length - i - 1; j++){
if(array[j] > array[j + 1]){
int tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
}
}
}
}对于冒泡排序,若已排好序,在这样排,实在浪费时间
可以建立一个flag判断,是否有进行排序操作,优化如下: public void bubbleSort(int[] array){
for(int i = 0; i < array.length - 1; i++){
boolean flag = false;
for(int j = 0; j < array.length - i - 1; j++){
if(array[j] > array[j + 1]){
int tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
flag = true;
}
}
if(!flag){
break;
}
}
}分析:
- 时间复杂度:O(N^2),优化后的代码在有序的情况下时间复杂度为O(N)
- 空间复杂度:O(1)
- 稳定性:稳定
- 思考:一种新手最容易上手的排序方式
堆排序
思路:
- 用待排序元素建立一个大根堆(降序建立小根堆)
- 交换下标为0的位置与最后一个元素的结点
- 继续向下调整为大根堆
- 再次交换时,交换下标0与最后一个元素的上一个元素
- 重复以上操作
- 直到下标为0位置与0位置交换时停止
代码如下:
//堆排序
public void heapSort(int[] array){
createBigHeap(array);
int end = array.length - 1;
while(end > 0){
//这里不需要在判断大小,因为大根堆最上面本来就是最大的,直接交换即可
swap(array, end, 0);
adjustmentDown(array, 0, end);
end--;
}
}
//创建大根堆
public void createBigHeap(int[] array){
int len = array.length;
for(int parent = (len - 1 - 1) / 2; parent >= 0; parent--){
adjustmentDown(array, parent, len);
}
}
//向下调整
public void adjustmentDown(int[] array, int parent, int len){
int child = parent * 2 + 1;
while(child < len){
//必须保证要有右孩子
if(child + 1 < len && array[child] < array[child + 1]){
child++;
}
if(array[parent] < array[child]){
swap(array, parent, child);
parent = child;
child = parent * 2 + 1;
}
else{
//如果根节点大于孩子结点后面就没必要比较了
break;
}
}
}
//交换
public void swap(int[] array, int i, int j){
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}分析:
- 时间复杂度:O(N * logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
- 思考:效率高了很多
快速排序(递归)
思路:(递归思路)
- 从元素集合中挑出一个数(“基准”)
- 将小于基准的数放到基准前面,大于基准的数放到基准后面,分完之后将基准放到分基准时停止的位置即可
- 递归将大于基准的子集合和小于基准的子集合用上述方法继续分配
如下代码:(递归,未优化)
//快速排序
//找基准
public int fundPivot(int[] array,int start, int end){
int key = array[start];
while(start < end){
//取等于号方式头尾元素相等造成死循环
//tart < end再次判断是因为,有可能end这边的值都比key大,最后越界访问
//一定要先从后面end遍历,最后结束位置的时候就把大的放前面了
while(start < end && key <= array[end]){
end--;
}
array[start] = array[end];
while(start < end && array[start] <= key){
start++;
}
array[end] = array[start];
}
//将基准放入停止时的位置
array[start] = key;
return start;
}
//分组递归
public void quick(int[] array, int left, int right){
if(left >= right){
return;
}
int pivot = fundPivot(array, left, right);
quick(array, left, pivot - 1);
quick(array, pivot + 1, right);
}
//充当个接口,同一传入的值为数组
public void quickSort(int[] array){
quick(array, 0, array.length - 1);
}存在的问题:当给的数据是有序(升序或降序)的,这时的快排时间复杂度会达到O(N^2),仅在元素集合是杂乱无章的情况下时间复杂度接近O(N*logN)为了解决这个问题,引入了三数取中法;
三数取中法思路:对待排序元素给定三个下标,第一个下标left指向最左边的元素,第二个下标right指向最右边的元素,第三个下标mid指向指向中间值-> (left + right) / 2,得到这三个下标后再求出这三个下标所指向的数据的中位数作为“基准”,这样找出的基准更可以将元素集合均分(基本就是二分),在数据有序情况下大大降低时间复杂度,趋近O(N*logN)。
如下代码:(第一步优化)
//快速排序
//找基准
public int fundPivot(int[] array,int start, int end){
int key = array[start];
while(start < end){
//取等于号方式头尾元素相等造成死循环
//tart < end再次判断是因为,有可能end这边的值都比key大,最后越界访问
//一定要先从后面end遍历,最后结束位置的时候就把大的放前面了
while(start < end && key <= array[end]){
end--;
}
array[start] = array[end];
while(start < end && array[start] <= key){
start++;
}
array[end] = array[start];
}
//将基准放入停止时的位置
array[start] = key;
return start;
}
//寻找中间值交换
public int funMidIndex(int[] array, int left, int right){
int mid = (left + right) / 2;
if(array[left] < array[right]){
if(array[mid] < array[left]){
return left;
}else if(array[right] < array[mid]){
return right;
}else{
return mid;
}
}else{
if(array[left] < array[mid]){
return left;
}else if(array[mid] < array[right]){
return right;
}else{
return mid;
}
}
}
//分组递归
public void quick(int[] array, int left, int right){
if(left >= right){
return;
}
int midIndex = funMidIndex(array, left, right);
swap(array, left, midIndex);
int pivot = fundPivot(array, left, right);
quick(array, left, pivot - 1);
quick(array, pivot + 1, right);
}
//充当个接口,同一传入的值为数组
public void quickSort(int[] array){
quick(array, 0, array.length - 1);
}存在问题:递归的层次太多,元素集合过大可能导致栈溢出;
解决办法:即使三数取中法一定程度上也减少了递归的深度,但是在庞大的数据下不足以支撑,减少递归层次;想象以下,递归最后一层实现了多少次递归呢?是2^(n - 1),而整个快速排序总共才递归2^n - 1,相当于最后一层递归就占了整个快排递归数量的一半多,不难想到,递归到结尾的时候,完全没有必要再递归下去,因为数据已经趋于有序,所以这个时候就可以用到插入排序,大大减少递归次数,防止栈溢出。
代码如下:(递归层次的优化)
//快速排序
//插入排序
public void insertSort(int[] array, int start, int end){
for(int i = start + 1; i <= end; i++){
int key = array[i];
int j = i - 1;
for(; j >= 0; j--){
if(array[j] > key){
array[j + 1] = array[j];
}else{
break;
}
}
array[j + 1] = key;
}
}
//找基准
public int fundPivot(int[] array,int start, int end){
int key = array[start];
while(start < end){
//取等于号方式头尾元素相等造成死循环
//tart < end再次判断是因为,有可能end这边的值都比key大,最后越界访问
//一定要先从后面end遍历,最后结束位置的时候就把大的放前面了
while(start < end && key <= array[end]){
end--;
}
array[start] = array[end];
while(start < end && array[start] <= key){
start++;
}
array[end] = array[start];
}
//将基准放入停止时的位置
array[start] = key;
return start;
}
//寻找中间值交换
public int funMidIndex(int[] array, int left, int right){
int mid = (left + right) / 2;
if(array[left] < array[right]){
if(array[mid] < array[left]){
return left;
}else if(array[right] < array[mid]){
return right;
}else{
return mid;
}
}else{
if(array[left] < array[mid]){
return left;
}else if(array[mid] < array[right]){
return right;
}else{
return mid;
}
}
}
//分组递归
public void quick(int[] array, int left, int right){
if(left >= right){
return;
}
//假设数据非常大
//这里相当于减少了7层递归
if(right - left + 1 <= 7){
insertSort(array, left, right);
}
int midIndex = funMidIndex(array, left, right);
swap(array, left, midIndex);
int pivot = fundPivot(array, left, right);
quick(array, left, pivot - 1);
quick(array, pivot + 1, right);
}
//充当个接口,同一传入的值为数组
public void quickSort(int[] array){
quick(array, 0, array.length - 1);
}分析:(最后一次优化)
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
- 思考:综合性能较高,适用于多种场合
快速排序(迭代)
思路:大致思路与递归相似,很多重复的东西下面就不细讲了(如三数取中法...)
- 建立一个栈,用来存放待排序区间的左右边界
- 可以通过三数去中法优化,然后找到“基准”
- 在基准的左边的元素个数不小于1的时候(否则视为有序),将基准左边区间的左右边界所指向的下标压入栈中,基准右边区间也是同样的操作
- 在栈不为空的前提下,弹出栈中两个元素,继续重复以上操作即可
代码如下:(经三数取中法优化)
//非递归快排
//寻找中间值交换
public int funMidIndex(int[] array, int left, int right){
int mid = (left + right) / 2;
if(array[left] < array[right]){
if(array[mid] < array[left]){
return left;
}else if(array[right] < array[mid]){
return right;
}else{
return mid;
}
}else{
if(array[left] < array[mid]){
return left;
}else if(array[mid] < array[right]){
return right;
}else{
return mid;
}
}
}
//找基准
public int fundPivot(int[] array,int start, int end){
int key = array[start];
while(start < end){
//取等于号方式头尾元素相等造成死循环
//tart < end再次判断是因为,有可能end这边的值都比key大,最后越界访问
//一定要先从后面end遍历,最后结束位置的时候就把大的放前面了
while(start < end && key <= array[end]){
end--;
}
array[start] = array[end];
while(start < end && array[start] <= key){
start++;
}
array[end] = array[start];
}
//将基准放入停止时的位置
array[start] = key;
return start;
}
public void quickSort(int[] array){
int left = 0;
int right = array.length - 1;
Stack stack = new Stack<>();
//三数取中法优化
int midIndex = funMidIndex(array, left, right);
swap(array, left, midIndex);
int pivot = fundPivot(array, left, right);
//若基准左边或右边的数据不超过一个,则将下标压入栈,否则就是有序
if(left + 1 < pivot){
stack.push(left);
stack.push(pivot - 1);
}
if(right - 1 > pivot){
stack.push(pivot + 1);
stack.push(right);
}
//只要栈不为空,就每次弹出栈顶的两个元素作为左右边界,继续进行如上操作
while(!stack.isEmpty()){
right = stack.pop();
left = stack.pop();
midIndex = funMidIndex(array, left, right);
swap(array, left, midIndex);
pivot = fundPivot(array, left, right);
if(left + 1 < pivot){
stack.push(left);
stack.push(pivot - 1);
}
if(right - 1 > pivot){
stack.push(pivot + 1);
stack.push(right);
}
}
} 归并排序(递归)
思路:
- 找到元素集合的中间下标,分成左段和右端(类似二叉树递归)
- 通过递归再继续将其左右段继续分为更小的子段
- 使每个子端有序
- 将分成的两路字段最后合并成一个新的有序的元素集合(具体实现过程看: 归并排序的迭代版本,下面有)
代码如下:
//归并排序
private void mergeFunc(int[] array, int left, int right){
if(left == right){
return;
}
int mid = (left + right) / 2;
//分解左边(包含mid下标元素)
mergeFunc(array, left, mid);
//分解右边
mergeFunc(array, mid + 1, right);
//合并
merge(array, left, right, mid);
}
//合并
private void merge(int[] array, int start, int end, int midIndex){
int[] tmpArr = new int[end - start + 1];
//tmpArr数组的零下标
int k = 0;
int s1 = start;
int s2 = midIndex + 1;
//两个同时比较
while(s1 <= midIndex && s2 <= end){
//这里因为是<=所以才是一个稳定的排序
if(array[s1] <= array[s2]){
tmpArr[k++] = array[s1++];
}else{
tmpArr[k++] = array[s2++];
}
}
//若比较完后,还剩余一方未比较完,直接将剩下的一方拼上
while(s1 <= midIndex){
tmpArr[k++] = array[s1++];
}
while(s2 <= end){
tmpArr[k++] = array[s2++];
}
//把排好序的数字从start处开始拷贝回原数组
for(int i = 0; i < k; i++){
array[i + start] = tmpArr[i];
}
}
public void mergeSort(int[] array){
mergeFunc(array, 0, array.length - 1);
}分析:
- 时间复杂度:严格意义上(不论是否有序)的O(N * logN)
- 空间复杂度:O(N)
- 稳定性:稳定
- 思考:空间复杂度大,不考虑空间的情况下适用
归并排序(迭代)
思路:(一定要注意指针下标的合理性)
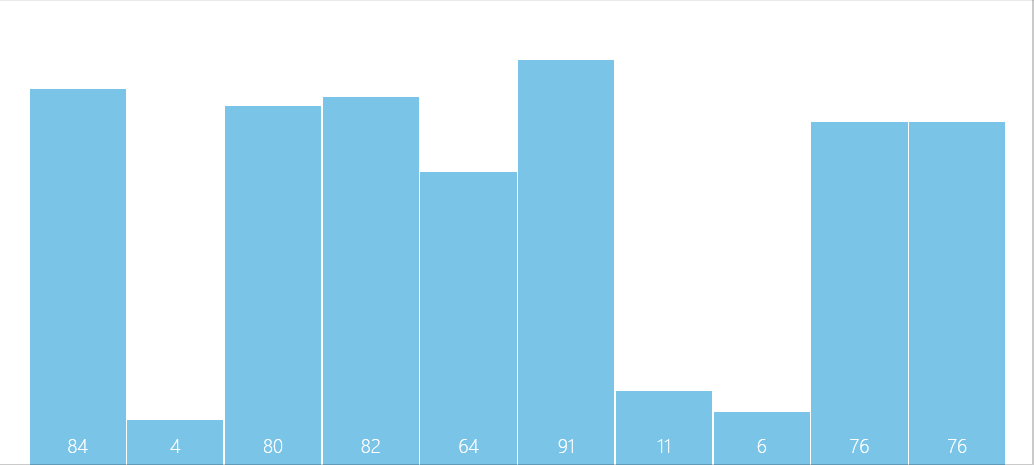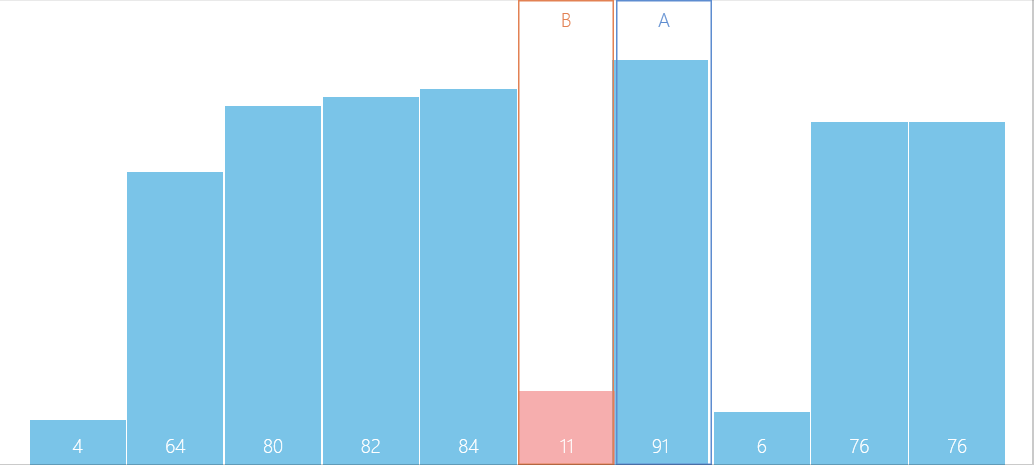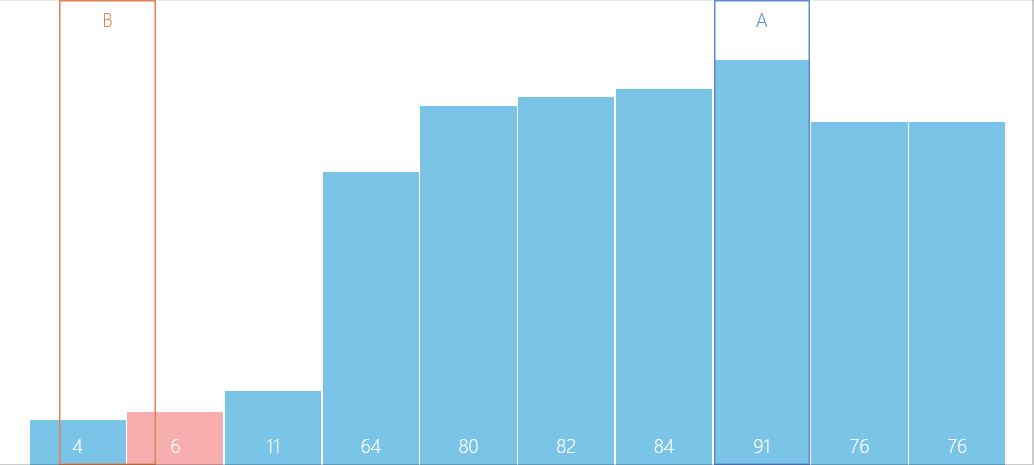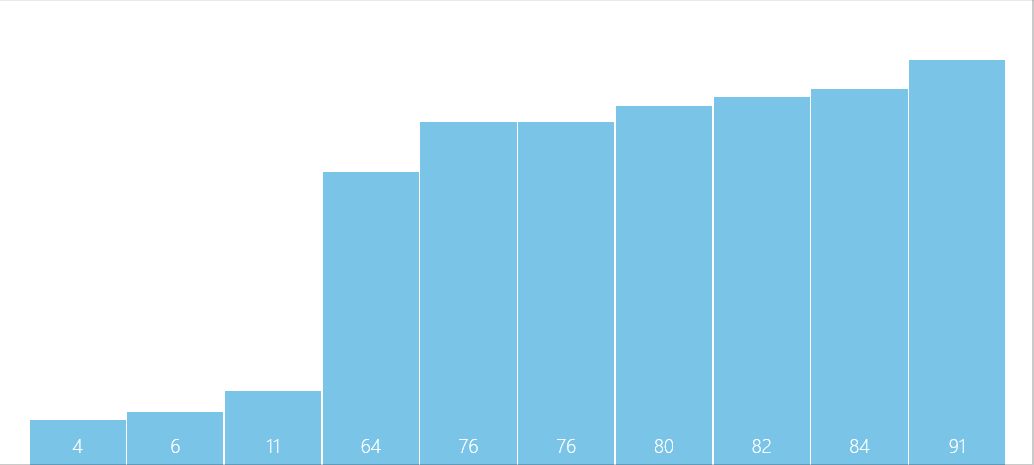
1.先将整个数据其分成一个数据为一组,共分为两组,如下图(红为一组,蓝为一组)
2.两组之间相互比较,并排序,如下图
3.再将组距放大一倍,相当于一组两个元素,如下图
4.给定指针如下图(一组一个元素的时候就有指针,当时表示用处不大,此时标注方便理解)
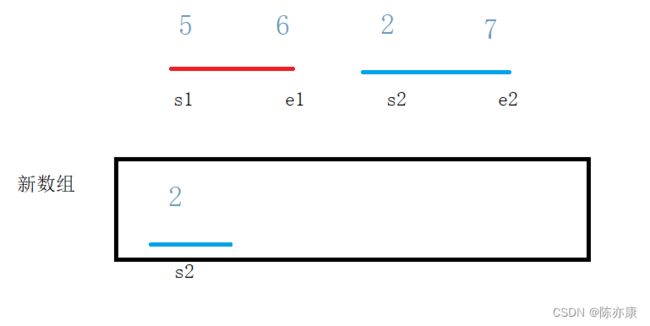
5.接下来就是合并两个有序的数组 :创建一个大小可以容纳所有元素的数组,先比较s1,s2谁小,将小的放入新数组,如下图
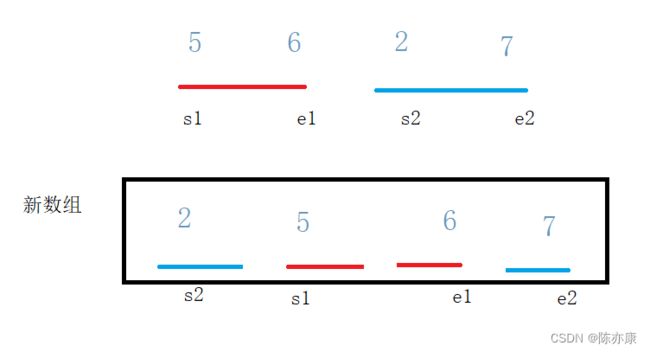
6.继续重复以上3~5操作,直到s1 > e1或s2 > e2时停止,若这两组,有一方先停止,就将剩下的一方直接从后加到数组中去 ,再继续扩到组距(直到大于数组总大小为止)...
代码如下:
//合并
private void merge(int[] array, int start, int end, int midIndex){
int[] tmpArr = new int[end - start + 1];
//tmpArr数组的零下标
int k = 0;
int s1 = start;
int s2 = midIndex + 1;
//两个同时比较
while(s1 <= midIndex && s2 <= end){
//这里因为是<=所以才是一个稳定的排序
if(array[s1] <= array[s2]){
tmpArr[k++] = array[s1++];
}else{
tmpArr[k++] = array[s2++];
}
}
//若比较完后,还剩余一方未比较完,直接将剩下的一方拼上
while(s1 <= midIndex){
tmpArr[k++] = array[s1++];
}
while(s2 <= end){
tmpArr[k++] = array[s2++];
}
//把排好序的数字从start处开始拷贝回原数组
for(int i = 0; i < k; i++){
array[i + start] = tmpArr[i];
}
}
public void mergeSort(int[] array){
int gap = 1;
while(gap < array.length){
// i+= gap*2 是为了保证s1可以跳过e2、s2、e2到下一个待排序位置
for(int i = 0; i < array.length; i += gap * 2){
//首先能进循环i一定合法
int s1 = i;
int e1 = i + gap - 1;
//注意保证指针不会越界!一旦越界采取强制措施,如下
if(e1 > array.length - 1){
e1 = array.length - 1;
}
int s2 = e1 + 1;
if(s2 > array.length - 1){
s2 = array.length - 1;
}
int e2 = s2 + gap - 1;
if(e2 > array.length - 1){
e2 = array.length - 1;
}
merge(array, s1, e2, e1);
}
gap *= 2;
}
}分析:
- 时间复杂度:严格意义上(不论是否有序)的O(N * logN)
- 空间复杂度:O(N)
- 稳定性:稳定
- 思考:空间复杂度大,不考虑空间的情况下适用
计数排序
思路:
- 通过待排序的元素集合找出最大值与最小值来确定计数数组的大小
- 通过遍历待排序数组,统计相同元素出现的次数(具体如上动态图)
- 遍历计数器数组,将统计出的结果回归到原序列中
代码如下:
public void countSort(int[] array){
int maxIndex = array[0];
int minIndex = array[0];
for(int i = 0; i < array.length; i++){
if(array[i] > maxIndex){
maxIndex = array[i];
}
if(array[i] < minIndex){
minIndex = array[i];
}
}
//假设最大值66,最小值60,则有66 - 60 = 6个数据,而60~66实际上有7个数据,所以加一
int[] countArr = new int[maxIndex - minIndex + 1];
//开始计数
for(int i = 0; i < array.length; i++){
countArr[array[i] - minIndex]++;
}
//写入原数组
int index = 0;//array的下标
for(int i = 0; i < countArr.length; i++){
while(countArr[i] != 0){
array[index] = i + minIndex;
countArr[i]--;
index++;
}
}
}分析:
- 时间复杂度:O(N + 数据范围)
- 空间复杂度:O(数据范围)
- 稳定性:很多资料上说是稳定的(博主这个代码是不稳定的)
- 思考:适合给定范围的数据进行排序,并且不需要比较元素之间的大小