poj 3321 Apple Tree
思路: 树状数组
分析:
1 题目给定一棵树,然后有n个树枝,每个树枝上面初始化有1个苹果,现在有m个操作
2 题目给定的是一棵树,我们应该考虑怎么把这棵树映射成一个数组,并且跟节点和儿子节点的编号是连续的。这一步我们可以利用dfs来做,利用时间撮的概念,第一次到达的时间作为起始的时间,第二次到达的时间为终点的时间,下图就是一个例子
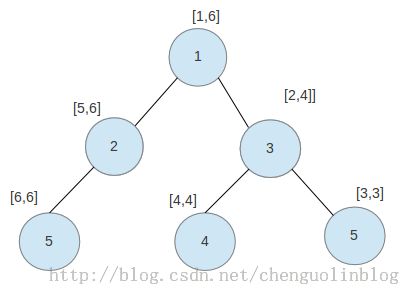 、
、
3 这一题的时间卡vector卡的紧,所以我们应该利用邻接表来存储图
4 当我们求出了每一个节点的时间戳之后,那么我们就可以利用树状数组来求,每一个点的时间戳区间就是这个节点的所有子树包括本身的和,那么这个和可以利用树状数组进行求解,更新的时候由于我们只要更新起始位置即可,这样能够保证是对的
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 100010;
struct Edge{
int x;
int y;
};
Edge e[MAXN];
int first[MAXN] , next[MAXN];
int n , step;
int num[MAXN];
int treeNum[MAXN];
int begin[MAXN] , end[MAXN];
bool vis[MAXN];
void dfs(int x){
vis[x] = true;
begin[x] = step;
for(int i = first[x] ; i != -1 ; i = next[i]){
if(!vis[e[i].y]){
step++;
dfs(e[i].y);
end[x] = step;
}
}
end[x] = step;
}
int lowbit(int x){
return x&(-x);
}
int getSum(int x){
int sum = 0;
while(x){
sum += treeNum[x];
x -= lowbit(x);
}
return sum;
}
void add(int x , int val){
while(x < MAXN){
treeNum[x] += val;
x += lowbit(x);
}
}
void init(){
step = 1;
memset(vis , false , sizeof(vis));
memset(treeNum , 0 , sizeof(treeNum));
for(int i = 1 ; i <= n ; i++){
first[i] = next[i] = -1;
num[i] = 1;
add(i , 1);
}
}
void solve(){
int m , x;
char c;
dfs(1);
scanf("%d%*c" , &m);
while(m--){
scanf("%c %d%*c" , &c , &x);
if(c == 'Q'){
int ans = getSum(end[x]);
ans -= getSum(begin[x]-1);
printf("%d\n" , ans);
}
else{
if(num[x])
add(begin[x] , -1);
else
add(begin[x] , 1);
num[x] = !num[x];
}
}
}
int main(){
scanf("%d" , &n);
init();
for(int i = 0 ; i < n-1 ; i++){
scanf("%d%d" , &e[i].x , &e[i].y);
int x = first[e[i].x];
next[i] = x;
first[e[i].x] = i;
}
solve();
return 0;
}