深度学习——生成对抗网络(GAN)
文章目录
- 什么是GAN(生成对抗网络)
- GAN的优化
-
- 鉴别器的优化
- 生成器的优化
- 公式角度理解什么是"对抗"
- GAN的训练
什么是GAN(生成对抗网络)
GAN分为生成器与鉴别器两部分,生成器将隐空间中的点作为输入,生成一张假图片。鉴别器会将真图片与假图片作为输入,鉴别出哪一张图片为真。
“对抗”即生成器与鉴别器之间的对抗,生成器企图利用生成的假图片欺骗鉴别器,鉴别器会依据生成的假图片与真图片的差距给生成器施加一个惩罚,生成器会利用这个惩罚优化自身,即进化,从而生成与真图片更相近的图片。而鉴别器依据生成器生成的更为真实的图片与真图片优化自身,即进化,从而进一步鉴别图片的真假。
GAN的优化
鉴别器的优化
鉴别器其实是一个分类器,用于判断一张图片是否为真图片,是一个二分类问题。设鉴别器为函数 D ( x ; θ 2 ) D(x;\theta_2) D(x;θ2),值为图片 x x x为真图片的概率, θ 2 \theta_2 θ2为鉴别器的参数。 P d a t a P_{data} Pdata为真图片符合的分布, G G G为假图片符合的分布,设
V ( D , G ) = E x ∼ P d a t a [ log D ( x ; θ 2 ) ] + E x ∼ G [ log ( 1 − D ( x ; θ 2 ) ) ] (式2.0) V(D,G)=E_{x \sim P_{data}}[\log D(x;\theta_2)]+E_{x \sim G}[\log(1-D(x;\theta_2))]\tag{式2.0} V(D,G)=Ex∼Pdata[logD(x;θ2)]+Ex∼G[log(1−D(x;θ2))](式2.0)
E x ∼ P d a t a [ log D ( x ; θ 2 ) ] E_{x \sim P_{data}}[\log D(x;\theta_2)] Ex∼Pdata[logD(x;θ2)]表示当鉴别器判断图片为真时,图片为真的期望。 E x ∼ G [ l o g ( 1 − D ( x ; θ 2 ) ) ] E_{x \sim G}[log(1-D(x;\theta_2))] Ex∼G[log(1−D(x;θ2))]表示鉴别器判断图片为假时,图片为假的期望。因此, V ( D , G ) V(D,G) V(D,G)表示鉴别器判断正确的期望。故鉴别器优化的目标为( G G G暂时看成定值,之后解释)
max D V ( D , G ) (式2.1) \max\limits_D V(D,G)\tag{式2.1} DmaxV(D,G)(式2.1)
设 P d a t a ( x ) P_{data}(x) Pdata(x)表示真图片的概率密度函数, G ( x ) G(x) G(x)表示假图片的概率密度函数,一张图片不能即是真图片,又是假图片,则式2.0可以写为
V ( D , G ) = ∫ x P d a t a ( x ) log D ( x ; θ 2 ) d x + ∫ x G ( x ) [ log ( 1 − D ( x ; θ 2 ) ) ] d x = ∫ x [ P d a t a ( x ) log D ( x ; θ 2 ) + G ( x ) log ( 1 − D ( x ; θ 2 ) ) ] d x (式2.2) \begin{aligned} V(D,G)=&\int_{x}P_{data}(x)\log D(x;\theta_2)dx+\int_{x}G(x)[\log(1-D(x;\theta_2))]dx\\ =&\int_{x}[P_{data}(x)\log D(x;\theta_2)+G(x)\log(1-D(x;\theta_2))]dx\tag{式2.2} \end{aligned} V(D,G)==∫xPdata(x)logD(x;θ2)dx+∫xG(x)[log(1−D(x;θ2))]dx∫x[Pdata(x)logD(x;θ2)+G(x)log(1−D(x;θ2))]dx(式2.2)
因此,最大化式2.1只需最大化 f ( D ) = P d a t a ( x ) log D ( x ; θ 2 ) + G ( x ) log ( 1 − D ( x ; θ 2 ) ) (式2.3) f(D)=P_{data}(x)\log D(x;\theta_2)+G(x)\log(1-D(x;\theta_2))\tag{式2.3} f(D)=Pdata(x)logD(x;θ2)+G(x)log(1−D(x;θ2))(式2.3)
其为凸函数,导数为0的点为取得最大值的点,则有
∂ f ( D ) ∂ D = P d a t a ( x ) 1 D ( x ; θ 2 ) + G ( x ) 1 1 − D ( x ; θ 2 ) ∗ ( − 1 ) = 0 \frac{\partial{f(D)}}{\partial{D}}=P_{data}(x)\frac{1}{D(x;\theta_2)}+G(x)\frac{1}{1-D(x;\theta_2)}*(-1)=0 ∂D∂f(D)=Pdata(x)D(x;θ2)1+G(x)1−D(x;θ2)1∗(−1)=0
求解上式可得
D ( x ; θ 2 ) = P d a t a ( x ) P d a t a ( x ) + G ( x ) (式2.4) D(x;\theta_2)=\frac{P_{data}(x)}{P_{data}(x)+G(x)}\tag{式2.4} D(x;θ2)=Pdata(x)+G(x)Pdata(x)(式2.4)
固定 G ( x ) G(x) G(x)的前提下,鉴别器只要拟合了式2.4,式2.1即有最大值,此时鉴别器优化的目标为 max θ 2 V ( D , G ) (式2.5) \max \limits_{\theta_2} V(D,G)\tag{式2.5} θ2maxV(D,G)(式2.5)
生成器的优化
假设所有的真图像都符合一个分布 P d a t a ( x ) P_{data}(x) Pdata(x),那生成器的目标就是尽可能的拟合该分布,设生成器的参数为 θ 1 \theta_1 θ1,其输出符合分布 G ( x ; θ 1 ) G(x;\theta_1) G(x;θ1),函数 d i v ( x , y ) div(x,y) div(x,y)可以判断分布 x x x与分布 y y y的差距(例如 K L KL KL散度),则生成器优化的目标为
min θ 1 d i v ( P d a t a ( x ) , G ( x ; θ 1 ) ) (式3.0) \min\limits_{\theta_1} div(P_{data}(x),G(x;\theta_1))\tag{式3.0} θ1mindiv(Pdata(x),G(x;θ1))(式3.0)
将式2.4代入式2.2可得
max V ( D , G ) = − 2 log 2 + ∫ x P d a t a ( x ) log 2 ∗ P d a t a ( x ) P d a t a ( x ) + G ( x ) d x + ∫ x P G ( x ) [ log 2 ∗ P G P d a t a ( x ) + G ( x ) ] d x = − 2 log 2 + 2 J S D ( P d a t a ( x ) ∣ ∣ G ( x ) ) (式3.1) \begin{aligned} \max V(D,G)=&-2\log2+\int_{x}P_{data}(x)\log \frac{2*P_{data}(x)}{P_{data}(x)+G(x)}dx+\int_{x}P_{G}(x)[\log \frac{2*P_{G}}{P_{data}(x)+G(x)}]dx\\ =&-2\log2+2JSD(P_{data}(x)||G(x))\tag{式3.1} \end{aligned} maxV(D,G)==−2log2+∫xPdata(x)logPdata(x)+G(x)2∗Pdata(x)dx+∫xPG(x)[logPdata(x)+G(x)2∗PG]dx−2log2+2JSD(Pdata(x)∣∣G(x))(式3.1)
JS散度和交叉熵一样,可以衡量两个分布之间的差异,鉴别器优化的最终结果 max V ( D , G ) \max V(D,G) maxV(D,G)即为判断生成器输出分布与真实图片分布之间的差距函数,此时生成器的优化目标为
min θ 1 max V ( D , G ) (式3.0) \min\limits_{\theta_1} \max V(D,G)\tag{式3.0} θ1minmaxV(D,G)(式3.0)
公式角度理解什么是"对抗"
从公式角度,我们来康康什么叫做”对抗“,GAN的训练如下
- 生成器进化完毕后, G G G固定,鉴别器依据生成器当前的分布更新自己的参数,结果为 max θ 2 V ( D , G ) \max \limits_{\theta_2} V(D,G) θ2maxV(D,G),此时鉴别器完成一轮进化,能最大程度区分真假图片。
- 鉴别器进化完毕后,可得 max V ( D , G ) \max V(D,G) maxV(D,G)(只有 G G G为自变量, D D D固定),表示生成器输出分布与真实分布的差异,生成器更新自己的参数为 min θ 1 max V ( D , G ) \min \limits_{\theta_1} \max V(D,G) θ1minmaxV(D,G),生成器完成一轮进化,能生成对于鉴别器而言,更具有欺骗性的图片(但不一定离拟合真实分布更近一步),这也是训练难点
可以证明,这么一个过程不断循环下去,最终会达到一个收敛状态,此时鉴别器对于一张图片,有50%概率判断为真,50%概率判断为假
GAN的训练
需要注意,对于鉴别器,会利用批量梯度下降训练多次,让鉴别器尽可能收敛。对于生成器,则只利用批量梯度下降训练一次,这是一个训练技巧。因为训练当前生成器至收敛,只能生成对于当前鉴别器而言,更具欺骗性的图片,而不是更加拟合真实分布,加速拟合的技巧之一就是减少生成器的训练次数。
值得注意的是,在现实训练中,我们无法得到连续随机变量的期望,因此我们使用了样本的均值作为总体期望的无偏估计进行计算,即
1 m ∑ i = 1 m log D ( x i ) ≈ E x ∼ P d a t a [ log D ( x ; θ 2 ) ] = ∫ x P d a t a ( x ) log D ( x ; θ 2 ) d x 1 m ∑ i = 1 m log ( 1 − D ( G ( z i ) ) ) ≈ E x ∼ G [ log ( 1 − D ( x ; θ 2 ) ) ] = ∫ x G ( x ) [ log ( 1 − D ( x ; θ 2 ) ) ] d x \begin{aligned} \frac{1}{m}\sum_{i=1}^m\log D(x_i)&\approx E_{x \sim P_{data}}[\log D(x;\theta_2)]=\int_{x}P_{data}(x)\log D(x;\theta_2)dx\\ \frac{1}{m}\sum_{i=1}^m\log(1-D(G(z_i)))&\approx E_{x \sim G}[\log (1-D(x;\theta_2))]=\int_{x}G(x)[\log(1-D(x;\theta_2))]dx \end{aligned} m1i=1∑mlogD(xi)m1i=1∑mlog(1−D(G(zi)))≈Ex∼Pdata[logD(x;θ2)]=∫xPdata(x)logD(x;θ2)dx≈Ex∼G[log(1−D(x;θ2))]=∫xG(x)[log(1−D(x;θ2))]dx
GAN并没有指明生成器与鉴别器的模型,这里简单介绍一下DCGAN,其利用卷积神经网络做为鉴别器与生成器,生成器的结构如下:
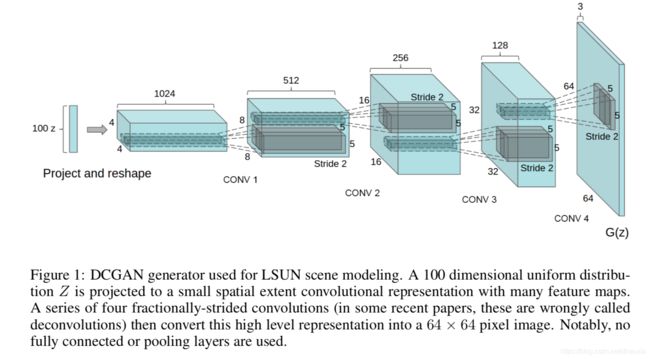
关于反卷积操作,可以查看pytorch的反卷积操作ConvTranspose2d
鉴别器是一个卷积神经网络,输入的图像经过若干层卷积后得到一个卷积特征,将得到的特征送入Logistic函数,输出可以看作是概率。
