FZU2082

树链剖分后要处理的是边的权值，而不是点的权值，但是只要边权下放到点，就可以了

如图

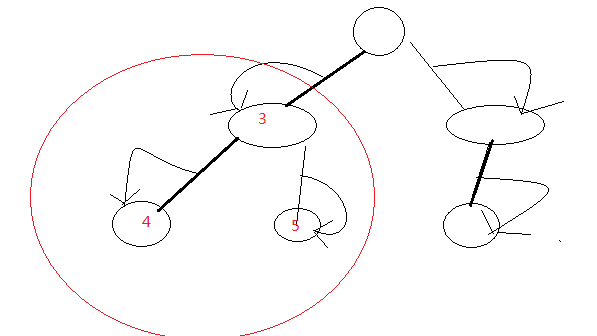
但是问题是，求图4->5路径的权值之和， 那么就会把点3给算进去

那么就要减去，

或者干脆不加进去

有两种方法

  1 #include <stdio.h>

  2 #include <string.h>

  3 #include <stdlib.h>

  4 #include <algorithm>

  5 #include <iostream>

  6 #include <queue>

  7 #include <stack>

  8 #include <vector>

  9 #include <map>

 10 #include <set>

 11 #include <string>

 12 #include <math.h>

 13 using namespace std;

 14 #pragma warning(disable:4996)

 15 #pragma comment(linker, "/STACK:1024000000,1024000000")

 16 typedef long long LL;                   

 17 const int INF = 1<<30;

 18 /*

 19 12 1

 20 1 2 1

 21 2 3 1

 22 3 4 1

 23 4 5 1

 24 5 11 1

 25 11 12 1

 26 1 6 1

 27 6 7 1

 28 7 8 1

 29 6 9 1

 30 6 10 1

 31 1 9 10

 32 */

 33 const int N = 50000 + 10;

 34 vector<int> g[N];

 35 int size[N], son[N], fa[N], depth[N], top[N], w[N], num, ra[N];

 36 LL tree[N*4];

 37 int edge[N][3];

 38 int h[N];

 39 void dfs(int u)

 40 {

 41     size[u] = 1;

 42     son[u] = 0;

 43     for (int i = 0; i < g[u].size(); ++i)

 44     {

 45         int v = g[u][i];

 46         if (v != fa[u])

 47         {

 48             fa[v] = u;

 49             depth[v] = depth[u] + 1;

 50             dfs(v);

 51             size[u] += size[v];

 52             if (size[v] > size[son[u]])

 53                 son[u] = v;

 54         }

 55     }

 56 }

 57 

 58 void dfs2(int u, int tp)

 59 {

 60     w[u] = ++num;

 61     ra[num] = u;

 62     top[u] = tp;

 63     if (son[u] != 0)

 64         dfs2(son[u], top[u]);

 65     for (int i = 0; i < g[u].size(); ++i)

 66     {

 67         int v = g[u][i];

 68         if (v != fa[u] && v != son[u])

 69             dfs2(v, v);

 70     }

 71     

 72 }

 73 void pushUp(int rt)

 74 {

 75     tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];

 76 }

 77 void update(int l, int r, int rt, int pos, int val)

 78 {

 79     if (l == r)

 80     {

 81         tree[rt] = val;

 82         return;

 83     }

 84     int mid = (l + r) >> 1;

 85     if (pos <= mid)

 86         update(l, mid, rt << 1, pos, val);

 87     else

 88         update(mid + 1, r, rt << 1 | 1, pos, val);

 89     pushUp(rt);

 90 }

 91 

 92 LL ans;

 93 void query(int l, int r, int rt, int L, int R)

 94 {

 95     if (L <= l&&R >= r)

 96     {

 97         ans += tree[rt];

 98         return;

 99     }

100     int mid = (l + r) >> 1;

101     if (L <= mid)

102         query(l, mid, rt << 1, L, R);

103     if (R > mid)

104         query(mid + 1, r, rt << 1 | 1, L, R);

105 }

106 int main()

107 {

108     int n, m, a, b, c;

109     while (scanf("%d%d", &n, &m) != EOF)

110     {

111         memset(tree, 0, sizeof(tree));

112         for (int i = 1; i <= n; ++i)

113             g[i].clear();

114         num = 0;

115         for (int i = 1; i < n; ++i)

116         {

117             scanf("%d%d%d", &edge[i][0], &edge[i][1], &edge[i][2]);

118             g[edge[i][0]].push_back(edge[i][1]);

119             g[edge[i][1]].push_back(edge[i][0]);

120         }

121         fa[1] = depth[1] = 0;

122         dfs(1);

123         dfs2(1, 1);

124         for (int i = 1; i < n; ++i)

125         {

126             if (depth[edge[i][0]] > depth[edge[i][1]])

127                 swap(edge[i][0], edge[i][1]);

128             h[edge[i][1]] = edge[i][2];

129             update(1, n, 1, w[edge[i][1]], edge[i][2]);

130         }

131         while (m--)

132         {

133             scanf("%d%d%d", &a, &b, &c);

134             if (a == 0)

135             {

136                 if (depth[edge[b][0]] > depth[edge[b][1]])

137                     swap(edge[b][0], edge[b][1]);

138                 update(1, n, 1, w[edge[b][1]], c);

139                 h[edge[b][1]] = c;

140             }

141             else

142             {

143                 ans = 0;

144                 while (top[b] != top[c])

145                 {

146                     if (depth[top[b]] < depth[top[c]])

147                         swap(b, c);

148                     query(1, n, 1, w[top[b]], w[b]);

149                     b = fa[top[b]];

150                 }

151                 //b和c一定是在一条链上

152                 if (depth[b]>depth[c])

153                     swap(b, c);

154                 

155                 

156                 //如果b有父亲，那么就有边下放到它，多加了这个点，要减去

157                 query(1, n, 1, w[b], w[c]);

158                 if (fa[b] != 0)

159                     ans -= h[b];

160                 /*

161                 如果b，c是在一条重链上， 那么询问w[son[b]] 到w[c]

162                 那么就没有加到点b

163                 否则，b，c就是指向同一点，那么w[son[b]] > w[c] , 询问是不会增加任何值的

164                 query(1, n, 1, w[son[b]], w[c]);

165                 */

166                 printf("%lld\n", ans);

167             }

168         }

169     }

170     return 0;

171 }

View Code