【论文阅读】Performer | Rethinking Attention With Performers
本文主要对Transformer一种改进方法“Performer”论文进行分析。
一、动机:Performer解决什么问题?
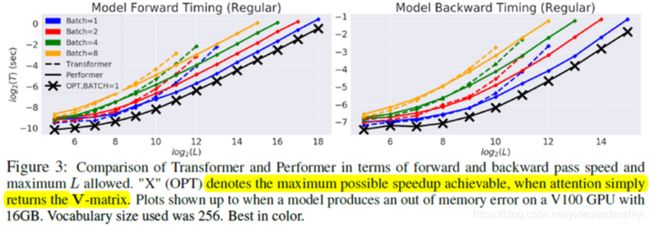
在NLP领域中,如果输入句子的长度是L,那么Transformer中的self-attention操作对应的时间复杂度和空间复杂度为O(L2)。Performer研究的就是采用怎样的近似方法,在尽量避免效果损失的情况下,得到线性的时间/空间复杂度,下图就是本文方法的近似效果。实线表示Performer得到的效果,虚线表示原始Transformer的效果,可以看出,当L变得非常大时,Performer的优势就体现出来了。
二、方法:具体是怎么实现的呢?
在常规的self-attention中,矩阵Query(Q)和矩阵Key(K)相乘,再通过softmax函数计算得到注意力矩阵Attention(A)。由于softmax函数中有非线性操作,因此A无法再返回原来的Q和K,但是可以将A分解成Q和K的随机非线性函数Q’和K’的乘积。
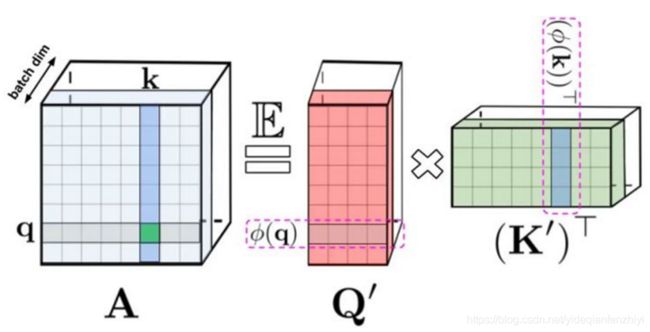
那么此时,self-attention操作就可以等效为下图等式右边的形式,其中d为embedding的维数,r为非线性映射的维数,通过运用矩阵乘法的交换律先计算K’和V,然后再乘上Q’,此时右边的时间复杂度变为O(Lrd),而本文假设情况就是L远大于r和d。
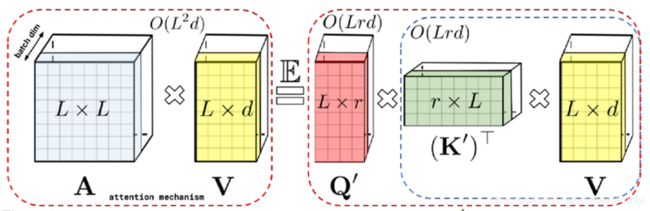
这样自然产生一个问题,如果先得到A,然后再将A分解成Q’和K’,计算复杂度并没有得到改变。在实际中,本文直接通过非线性函数的映射,由Q和K分别得到Q’和K’,而无需显式地构建二次方尺寸的注意力矩阵A,从而将复杂度降到了线性,本文将该方法称之为FAVOR+ (Fast Attention Via positive Orthogonal Random features)。
我们这里对FAVOR+中的关键词进行逐一分析:
——“Fast Attention” 指的是便是时间复杂度相比于传统的方式得到明显降低;
Attention的经典形式为
s o f t m a x ( Q K T / d ) ∗ V softmax(QK^{T} / \sqrt{d})*V softmax(QKT/d)∗V
为了方便推出本文的方法,本文对该式进行了重新整理,以下是其等价表达式:
![]()
其中 d i a g diag diag是将一个输入向量变成对角矩阵, 1 L 1_L 1L则是一个长度为L值全为1的向量。
不考虑常数d,对Q和K中任一向量 q i q_i qi和 k j k_j kj,其相似性度量为 e x p ( q i ∗ k j ) exp(q_i∗k_j) exp(qi∗kj), 引入核方法:
K ( x , y ) = E [ ϕ ( x ) T ϕ ( y ) ] K(x, y) = \mathbb{E}[\phi(x)^T \phi(y)] K(x,y)=E[ϕ(x)Tϕ(y)]
这里是对核方法进行逆向的使用,寻找到一种特征映射,能够等效于核方法,以下是论文中的描述:

关键问题是:如何找到这个特征映射呢?
——“Positive Random Features”,则是指本文找到了一组随机特征映射的方式,能够实现上面的功能,并且映射后的值都为positive(正值)
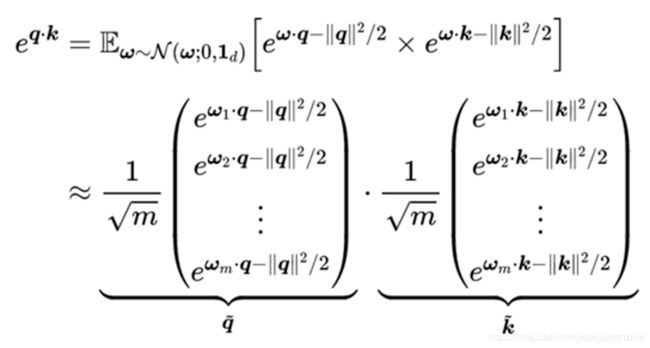
这里的m就是上面提到的r, 当m取值较少时,映射后的特征维数就越低,此时计算复杂度也降低越低,但效果可能会变得更差,所以需要选择合适的映射特征维数。本文指出,这种方式是一种无偏近似,同时能够保证得到的结果是正值,因为原始的Attention矩阵中每个元素按理来说都应该是正数,相关证明可见论文附录。
——“Orthogonal” 是指在进行随机特征映射的各个方向需要正交
在线性近似中, ω 1 \omega_1 ω1, ω 2 \omega_2 ω2, …, 是独立重复地从 N ( ω ; 0 , 1 d ) \mathcal{N} (\omega; 0, 1_d) N(ω;0,1d) 中采样出来的,而原论文则指出,如果将各个 ω i \omega_i ωi 进行正交化,能有效地降低估算的方差,并提高单次估算的平均精度。本文采用的Gram-Schmidt重归一化,不管使用什么分布,都能保证无偏性(证明见[7])。如果要降低估算的方差,那么就应该要降低采样的随机性,使得采样的结果更为均匀一些。而各个向量正交化,是方向上均匀的一种实现方式。
本文用了大量的篇幅从理论上证明FAVOR+近似的有效性。
大家感兴趣可以参考原文。
三、实验结果:效果咋样?
——Computational Costs
Performer相对于Transformer速度上优势明显,尤其是输入比较长的时候。

其中带x的表示最大可能的加速情况,此时直接返回的是V矩阵。
——Softmax Attention Approximation Error
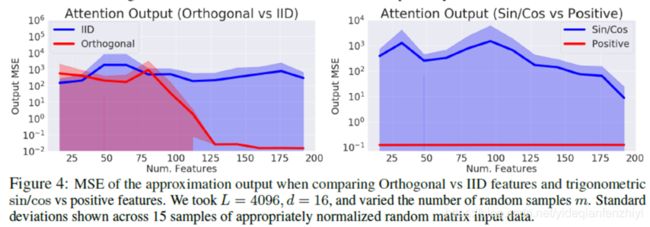
该实验是衡量对Attention矩阵的近似误差,左图是独立同分布和正交的对比,右图则是sin/cos和positive的对比。可以看到,Performer中的正交和positive特性都是必不可少的。从左图可以看出,当feature的数量是125及以上时,Attention矩阵才能被很好地近似。
——Softmax Approximation On Transformers
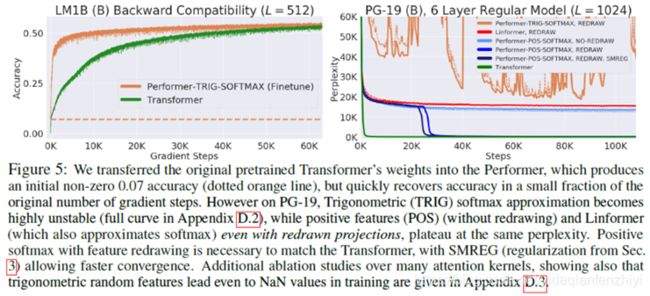
直接将训练好的Transformer转成Performer,效果会降低,不过经过对 Performer进行fine-tune可以快速还原到原来Transformer的结果。同时更快,见下面左图。同时,正值特性是必不可少的,用sin/cos会导致loss不稳定,见下面右图。
四、总结
Performer通过将指数操作进行拆分近似,换取了两种优化:
1)近似算法上的优化,使用尽可能小的r来达到。
2)矩阵乘法结合律上的优化。
在保证近似的程度上,使用了核技法、正值和正交技巧。
短序列用 Performer 性能应该是下降的,当L非常大的时候,效果才明显。Performer(包括其他的线性 Attention)跟相对位置编码是不兼容的,因为相对位置编码是直接加在 Attention 矩阵里边的,Performer 连 Attention 矩阵都没有,自然是加不了的。
五、扩展:各种Transformer改进版
近些年随着Transformer在NLP领域大行其道,出现了很多Transformer的改进版[2][3]:


下图表示Transformer及各种改进模型的**“性能-速度-显存”**图,纵轴是性能,横轴是速度,圆圈的大小代表所需要的显存。理论上来说,越靠近右上方的模型越好,圆圈越小的模型越好。

其中Big bird效果不错,它的核心思想是将多种attention方式相结合[8]。

六、参考资料
[1] Choromanski K, Likhosherstov V, Dohan D, et al. Rethinking attention with performers[J]. arXiv preprint arXiv:2009.14794, 2020. [Link]
[2] Tay Y, Dehghani M, Bahri D, et al. Efficient transformers: A survey[J]. arXiv preprint arXiv:2009.06732, 2020.
[3] Tay Y, Dehghani M, Abnar S, et al. Long Range Arena: A Benchmark for Efficient Transformers[J]. arXiv preprint arXiv:2011.04006, 2020.
[4] 苏剑林, Performer:用随机投影将Attention的复杂度线性化
[5]张雨石, Performer: 基于正交随机特征的快速注意力计算
[6] 学术头条,Performer带头反思Attention,大家轻拍!丨ICLR2021
[7] Krzysztof Marcin Choromanski, Mark Rowland, and Adrian Weller. The unreasonable effectiveness of structured random orthogonal embeddings. NIPS2017.
[8] Zaheer M, Guruganesh G, Dubey A, et al. Big bird: Transformers for longer sequences[J]. arXiv preprint arXiv:2007.14062, 2020.