机器学习实战笔记——决策树
决策树 - ID3
决策树也是经常使用的数据挖掘算法。
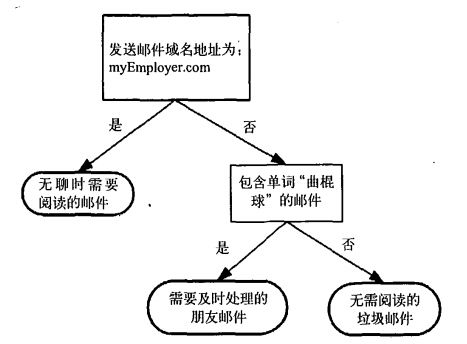
这张图所示就是一个决策树。长方形代表判断模块,椭圆形代表终止模块。从判断模块引出的左右箭头称作分支。
决策树的一个重要任务是为了理解数据中所蕴含的知识信息,因此决策树可以使用不熟悉的数据集合,并从中提取出一系列,这些机器根据数据集创建规则的过程,就是机器学习的过程。
训练出来的数据可以使用Matplotlib来绘制决策树图。
决策树构造
算法特点:
- 优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
- 缺点:可能会产生过拟合的问题。
- 适用数据类型:数值型和标称型。
首先需要学习数学上如何适用信息论划分数据集,然后编写代码将理论应用到具体的数据集上,最后编写代码构建决策树。
在构造决策树时,我们需要解决的第一个问题就是,当前数据集上哪个特征在划分数据分类时起决定作用。其实就是根据特征进行划分子集,再根据第二特征进行划分。这里面比较重要的是如果排序特征,找特征的依据是是么:
- 数量最多的特征
- 按照特征分组最少的特征
- 按特征,分组之间的距离最大,信息熵最大。
分组的结束条件是数据子集中的数据属于同一个类型,否则就需要进行重新划分数据子集。所以决策树就是一个递归的过程。
检测数据集中每个子项是否属于同一分类:
If so return 类标签
else
寻找数据集的最好特征
划分数据集
创建分支节点
for 每个新划分的子集
调用自己进行下一轮的划分,并将结果加入到分支节点上
return 分支节点决策树的一般流程:
- 收集数据
- 准备数据:只适用标称型,因此数值型数据必须离散化。
- 分析数据
- 训练算法:构造树的数据结构
- 测试算法
- 适用算法:此步骤可以适用于任何监督学习算法。
一些决策树算法采用二分法划分数据,也可以使用属性拆分出几个分类来识别出有几个分支。
信息增益
划分数据集的大原则是:将无序的数据变得更加有序,这就是信息熵的作用!在划分数据集之前之后信息发生的变化称为信息增益。获得信息增益最高的特征就是最好的选择。
熵定义为信息的期望值,如果待分类的事务可能划分在多个分类中,则符号xi的信息定义为:
其中p(xi)是选择该分类的概率。为了计算熵,需要计算所有类别所有可能值包含的信息期望值,通过下面的公式得到:
其中n是分类的个数。下面给定一个指定数据集的信息熵的计算代码:
from math import log
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1] # 最后一个元素放置的是这条记录的结果或者标签。[1,2,yes]
if currentLabel not in labelCounts.keys:
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2)
return shannonEnt熵越高,则混合的数据也越多,我们可以在数据集中添加更多的分类,观察熵是如何变化的。得到熵之后,我们就可以按照获取最大信息增益的方法划分数据集。
另一个度量集合无序程度的方法是基尼不纯度,简单地说就是从一个数据集中随机选取子项,度量其被错误分类到其他分组里的概率。
划分数据集
我们将对每个特征划分数据集的结果计算一次信息熵,然后判断按照哪个特征划分数据集是最好的划分方式。
其实这里面是按照单个特征进行的划分,也许存在组合特征的这种形式,特征组合又该如何找到答案呢?这个地方是不是应该使用朴素贝叶斯理论。
递归结束的条件是:程序遍历完所有划分数据集的属性,或者每个分支下的所有实例都具有相同的属性。
我们可以设置算法可以划分的最大分组数目。当然还有其他的决策树算法,如ID3、C4.5和CART;这些算法不总是在每次划分分组时都会消耗特征。由于特征数目并不是在每次划分数据分组时都减少,因此这些算法在实际使用时可能引起一定的问题。
如果数据已经处理了所有属性,但是类标签依然不是唯一的,此时我们需要决定如何定义该叶子节点,在这种情况下,我们通常会采用多数表决的方法决定该叶子节点。(是否可以递归解决这个问题,是不是没有找到更关键的特征,这个都是可以考虑的优化点吧!,也可以考虑组合特征解决这个问题)。
使用MatplotLib画出最后的决策树
略
问题
生成的决策树,可能匹配项太多了。我们称这个问题为过度匹配。为了减少过度匹配的问题,我们可以裁剪决策树,去掉一些不必要的叶子节点。
本章使用的算法是ID3算法,ID3算法用于划分标称型数据集;构建决策树时,我们通常采用递归的方法进行构造。
还有其他的构造树算法,比如C4.5,CART等。
其他
关于Cart决策树算法的其他介绍:https://blog.csdn.net/jiede1/article/details/76034328