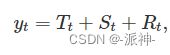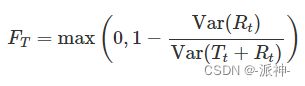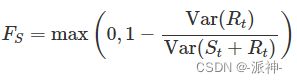时间序列的数据分析(四):STL分解

之前已经完成了三篇关于时间序列的博客，还没有阅读过的读者请先阅读：

1. 时间序列的数据分析(一):主要成分

2. 时间序列的数据分析(二):数据趋势的计算

3. 时间序列的数据分析(三):经典时间序列分解 

六. STL分解

6.1 主要参数

STL（Seasonal and Trend decomposition using Loess）是一个非常通用和稳健强硬的分解时间序列的方法，其中Loess是一种估算非线性关系的方法。STL分解法由 R. B. Cleveland, Cleveland, McRae, & Terpenning (1990)提出。STL也是将时间序列分解成三个主要分量: 趋势、季节项和残差 。STL使用LOESS(locally estimated scatterplot smoothing) 来提取三个分量的平滑估计，在python中实现时间序列的STL分解主要是通过调用statsmodels类库的STL方法来实现的，该STL方法有四个主要的输入参数：

• endog：表示需要分解的数据集,它是STL方法的第一个参数，该数据集的类型可以是numpy的array,也可以是pandas的series 或者dataframe.
• period：表示季节性周期，如果endog的类型是numpy的array则需要指定period，如果是pandas的series 或dataframe则stl方法可以根据索引推断出period,因此无需指定peroid
• season： 表示季节性平滑器的长度，它必须是一个奇数，通常要>=7(默认)。
• trend：表示趋势平滑器的长度,通常要>period(或season)的1-1.5倍，并且它必须是一个奇数。默认值是最小的1-1.5倍的period,比如period=7则trend默认值是9，如果period=12则trend默认值是13

6.2 分解过程

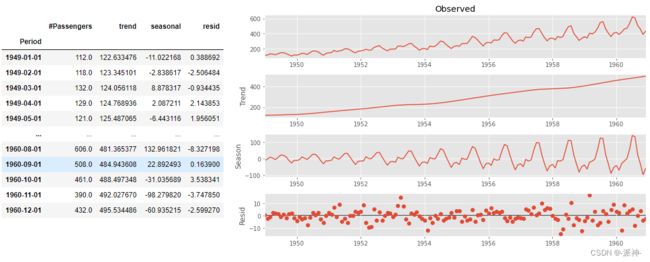
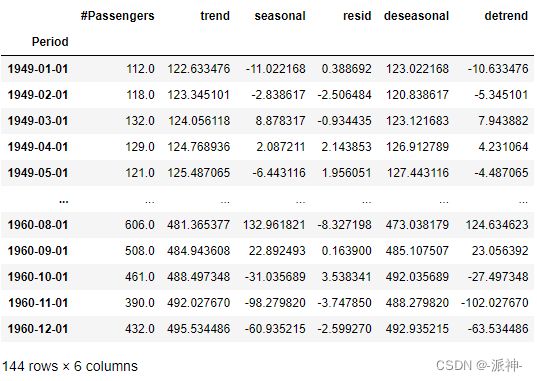
下面我们使用statsmodels的STL方法对航空公司乘客数据进行分解并获取各个分量的结果：

from statsmodels.tsa.seasonal import STL
plt.rc("figure", figsize=(10, 6))

df=pd.read_csv("airline_Passengers.csv")
df['Period']=pd.to_datetime(df['Period'])
df.set_index('Period',inplace=True)

res = STL(df).fit()
res.plot()

df['trend']=res.trend
df['seasonal']=res.seasonal
df['resid']=res.resid

 

 这里的STL方法中我们只使用了第一个参数，其它均为默认参数,因为我们的数据集是dataframe，因此STL方法可以根据datetime的索引列推断出peroid，如果数据类型是numpy的array那就必须指定peroid。下面我们可以观察一下残差的分布以及它的均值，一般情况下如果残差呈现出以0为均值的近似正太分布(这不是必须的)那么说明我们使用了正确的分解方法。

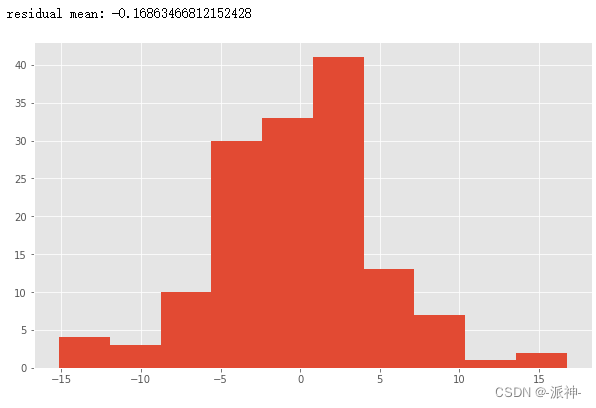
print('residual mean:',df.resid.mean())
df.resid.hist();

 从上面的结果可知我们的残差近似正太分布并且均值在0的附近,这说明SLT分解是正确的。

 6.3 趋势性、季节性程度及季节项波峰的计算

时间序列数据可以被分解为:趋势(Trend)、季节性(seasonal)、残差(residual),其分解式一般可以表示为:

 其中T(t)表示t时刻的趋势值,S(t)表示t时刻的季节项值,R(t)表示t时刻的残差值。对于趋势性很强的数据，经季节调整后(删除季节项)的数据应比残差项的变动幅度更大。因此，会相对较小。但是，对于没有趋势或是趋势很弱的时间序列，两个方差应大致相同。因此，我们将趋势强度定义为：

 这可以给趋势强度的衡量标准，其值在 0-1 之间。因为有些情况下残差项的方差甚至比季节变换后的序列还大，我们令可取的最小值为0。

相似地，季节性的强度定义如下，其所用的数据为去除趋势后的数据而不是去除季节后的数据。

当季节强度接近 0 时表示该序列几乎没有季节性，当季节强度接近 1 时表示该序列的 远小于 。

在时间序列中季节性一般呈现周期性变化的规律,因此季节性周期中的波峰大体上也是固定的，因此我们只需要找到季节性周期中的最大值就可以确定波峰期。

下面我们来计算一下趋势程度、季节性程度以及季节性波峰期，首先我们需要在数据中删除趋势项和季节项并得到两个新列:detrend和deseasonal，其中detrend列表示, 而deseasonal表示:

#从数据中删除趋势项
df['detrend']=df['#Passengers']-df.trend
#从数据中删除季节项
df['deseasonal']=df['#Passengers']-df.seasonal

接下来我们套用公式来计算趋势和季节性程度：

trend_strength=max(0,1-df.resid.var()/df.deseasonal.var())
seasonal_strength=max(0,1-df.resid.var()/df.detrend.var())
print('trend_strength:',trend_strength)
print('seasonal_strength:',seasonal_strength)

 

 从结果中我们看到数据中的趋势和季节性程度都非常高(接近1)，趋势和季节性程度越高,那说明数据的可预测性越好。接下来我们来计算季节性波峰：

period=12
peak = (np.argmax(df.seasonal) + 1) % period
peak = period if peak == 0 else peak

print("peak:",peak)

 

波峰值为7，说明改每年的7月为波峰期,这个从数据趋势图中也能得到确认。

总结

今天我们主要介绍了STL的分解的主要参数,和分解的过程，并观察了分解以后残差的分布和均值并确认了残差服从以0为均值的近似正太分布,这说明STL分解是正确的。其次我们还介绍了趋势程度、季节性程度以及季节性波峰的计算方法，这有助于确定数据是否具有良好的可预测性。

参考资料

statsmodels.tsa.seasonal.STL — statsmodels 

Seasonal-Trend decomposition using LOESS (STL) — statsmodels

https://www.scb.se/contentassets/ca21efb41fee47d293bbee5bf7be7fb3/stl-a-seasonal-trend-decomposition-procedure-based-on-loess.pdf