记录深度学习（五）----最小二乘法与梯度下降原理及实现

1、机器学习中的建模思想----以线性回归为例

我们在学习机器学习过程中，往往更关注那些复杂的模型和算法，忽略了机器学习底层的朴素的思想。机器学习基本的思想可以归类为以下：

• step1、提出你的模型
  如本节中，我们试图利用一条直线（y=ax+b）去拟合二维平面空间中的点，这里我们所使用的这条直线，就是我们提出的基本模型。而在后续的深度学习的学习过程中，我们还将看到更为强大、同时也更加通用的神经网络模型。当然，不同的模型能够适用不同的场景，在提出模型时，我们往往会预设一些影响模型结构或者实际判别性能的参数，如简单线性回归中的a和b；
• step2、确定损失函数和目标函数
  接下来，围绕建模的目标，我们需要合理设置损失函数，并在此基础之上设置目标函数，当然，在很多情况下，这二者是相同的。例如，在上述简单线性回归中，我们的建模目标就是希望y=ax+b这条直线能够尽可能的拟合(1,2)、(3,4)这两个点，或者说尽可能“穿过”这两个点，因此我们设置了SSE作为损失函数，也就是预测值和真实值的差值平方和。当然，在计算过程中不难发现，SSE是一个包含了a和b这两个变量的方程，因此SSE本身也是一个函数（a和b的二元函数），并且在线性回归中，SSE既是损失函数（用于衡量真实值和预测值差值的函数），同时也是我们的目标函数（接下来需要优化、或者说要求最小值的函数）。这里尤其需要注意的是，损失函数不是模型，而是模型参数所组成的一个函数。
• step3、根据目标函数特性，选择优化方法，求解目标函数
  目标函数既承载了我们优化的目标（让预测值和真实值尽可能接近），同时也是包含了模型参数的函数，因此完成建模需要确定参数、优化结果需要预测值尽可能接近真实值这两方面需求就统一到了求解目标函数最小值的过程中了，也就是说，当我们围绕目标函数求解最小值时，也就完成了模型参数的求解。当然，这个过程本质上就是一个数学的最优化过程，求解目标函数最小值本质上也就是一个最优化问题，而要解决这个问题，我们就需要灵活适用一些最优化方法。当然，在具体的最优化方法的选择上，函数本身的性质是重要影响因素，也就是说，不同类型、不同性质的函数会影响优化方法的选择。在简单线性回归中，由于目标函数是凸函数，我们根据凸函数性质，判断偏导函数取值为0的点就是最小值点，进而完成a、b的计算（也就是最小二乘法），其实就是通过函数本身的性质进行最优化方法的选取

我们以最简单的线性回归为例讲解如上述的步骤，
有这样的数据

x	y
5	6
7	8

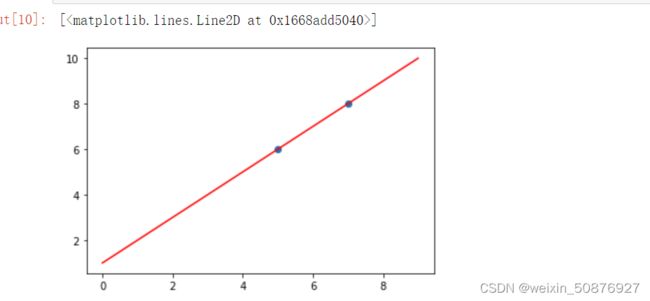
我们希望通过一条直线去拟合它。y = ax+b

x	y	yhat
5	6	5a+b
7	8	7a+b

这条直线应该满足y_hat与y之间的误差最小。这就引出了我们的损失函数。SSE

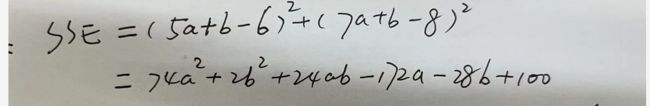
使得损失函数最小的a,b值就是我们模型的解。上述的SSE是个典型的凸函数,而求解凸函数的最小值常用的优化方法就是最小二乘法：

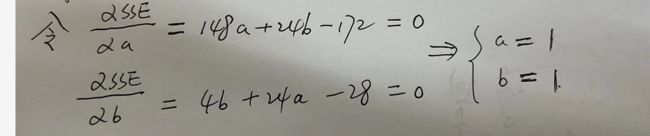
import matplotlib.pyplot as plt
import numpy as np

x1=[5,7]
y1 =[6,8]
x = np.arange(0,10,1)
y = x+1
plt.scatter(x1,y1)
plt.plot(x,y,'r')

2、最小二乘法

2.1、最小二乘法的矩阵表示

2.2、最小二乘法的实现

我们用上面的例子来编程实现以下：

import torch 
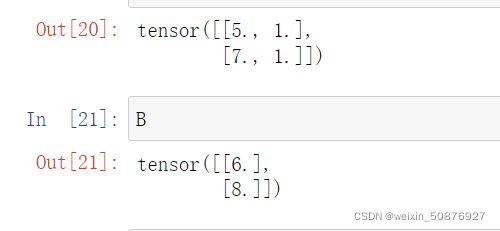
A = torch.tensor([[5,1],[7,1]],dtype =torch.float32)
B =torch.tensor([6,8],dtype =torch.float32 ).reshape(2,1)
print(A)
pritn(B)

w = torch.mm(torch.mm(torch.inverse(torch.mm(A.t(),A)),A.t()),B)
w

与手动算的结果一致。还可以反向验证以下，求导autograd模块

a = torch.tensor(1.,requires_grad = True)# 创建一个可导的张量
b = torch.tensor(1.,requires_grad = True)
sse = torch.pow((5*a+b -6), 2) + torch.pow((7*a+b-8), 2)
torch.autograd.grad(sse,[a, b])

sse函数在（1，1）处的偏导数为0.

3、梯度下降

最小二乘法虽然高效并且结果精确，但也有不完美的地方，核心就在于最小二乘法的使用条件较为苛刻，要求特征张量的交叉乘积结果必须是满秩矩阵，才能进行求解。而在实际情况中，很多数据的特征张量并不能满足条件，此时就无法使用最小二乘法进行求解。

鉴于许多目标函数本身也并不存在最小值或者唯一最小值，在优化的过程中略有偏差也是可以接受的。当然，伴随着深度学习的逐渐深入，我们会发现，最小值并不唯一存在才是目标函数的常态。基于此情况，很多根据等式形变得到的精确的求解析解的优化方法（如最小二乘）就无法适用，此时我们需要寻找一种更加通用的，能够高效、快速逼近目标函数优化目标的最优化方法。在机器学习领域，最通用的求解目标函数的最优化方法就是著名的梯度下降算法。

值得一提的是，我们通常指的梯度下降算法，并不是某一个算法，而是某一类依照梯度下降基本理论基础展开的算法簇，包括梯度下降算法、随机梯度下降算法、小批量梯度下降算法等等。接下来，我们就从最简单的梯度下降入手，讲解梯度下降的核心思想和一般使用方法。
先来了解一下反向传播的知识，这是完成梯度下降的基础。

x = torch.tensor(1.,requires_grad = True)
y = x**2
z = y + 1
z

z.backward()
x.grad

z = x**2 +1 在x = 1时的导数值为2

梯度下降的基本思想其实并不复杂，其核心就是希望能够通过数学意义上的迭代运算，从一个随机点出发，一步步逼近最优解

3.1、梯度下降的矩阵表示

接着最小二乘法的矩阵表示，：

3.2、梯度下降的实现

# 手动实现简单的梯度下降,沿用上述的A，B
#1、设置初试参数
w = torch.zeros(2, 1, requires_grad = True)#默认初始梯度为（0，0）
A = torch.tensor([[5,1],[7,1]],dtype =torch.float32,requires_grad = True)#这是特征矩阵
B =torch.tensor([6,8],dtype =torch.float32 ,requires_grad = True).reshape(2,1)#这是真实的y值
#设置步长
eps = torch.tensor(0.01, requires_grad = True)
# 梯度计算公式
grad = torch.mm(A.t(), (torch.mm(A, w) - B))/2
grad

#更新梯度
w = w - eps * grad
w

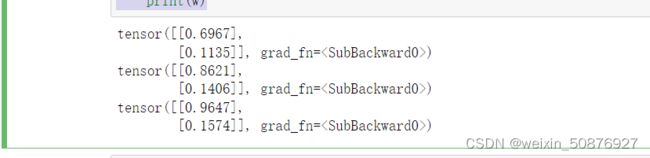
for k in range(3):
    grad = torch.mm(A.t(), (torch.mm(A, w) - B))/2
    w = w - eps * grad
    print(w)

#迭代10000次看看
for k in range(10000):
    grad = torch.mm(A.t(), (torch.mm(A, w) - B))/2
    w = w - eps * grad
w 

逼近最优解，迭代30000次左右看看，