从零实现深度学习框架——Seq2Seq从理论到实战【理论】

引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不使用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

本文介绍seq2seq模型，由论文Sequence to Sequence Learning with Neural Networks提出，能解决输入和输出序列长度不等的任务——机器翻译、自动摘要、自动问答等。

博主针对该经典论文提供了中文翻译：[论文翻译]Sequence to Sequence Learning with Neural Networks

Seq2Seq

Seq2Seq网络即sequence to sequence，序列到序列网络，输入一个序列，输出另一个序列。这个架构重要之处在于，输入序列和输出序列的长度是可变的。

Seq2Seq使用的具体方法基本都属于编码器-解码器模型。

其核心思想是通过编码器(Encoder)将输入序列编码成一个定长的向量表示，也称为具有上下文信息的表示，简称为上下文(context)。然后将上下文向量喂给解码器(Decoder)，来生成任务相关的输出序列。

总结一下，编码器-解码器架构包含三个组件：

• 编码器接收一个输入序列，$x_1^n$，然后生成对应的上下文表示，$h_1^n$。常用于编码器的网络可以为RNN、CNN或Transformer等。
• 上下文向量$c$，由一个函数基于$h_1^n$生成，传递输入的核心信息到解码器。
• 解码器接收$c$作为输入，然后生成一个任意长度的隐藏状态序列$h_1^m$，从中可以得到对应的输出$y_1^m$。和编码器一样，也有多种实现方案。

基于RNN实现编码器-解码器

[翻译]Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation使用RNN作为编码器和解码器实现机器翻译。

我们本小节来看如何通过RNN来实现编码器-解码器网络。

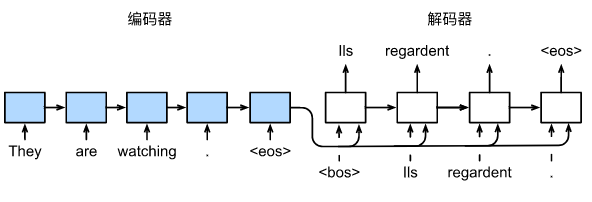
实际上会有两个不同的RNN网络，一个作为编码器，将变长的输入序列转换为定长的编码(上下文向量)；另一个作为解码器，通过该上下文向量连续生成输出序列，基于输入序列的编码信息和输出序列已经生成的单词来预测一下单词。上图演示了如何在机器翻译中使用两个RNN进行序列号序列学习。

这里有两个特殊单词和，分别表示序列结束和开始标志。

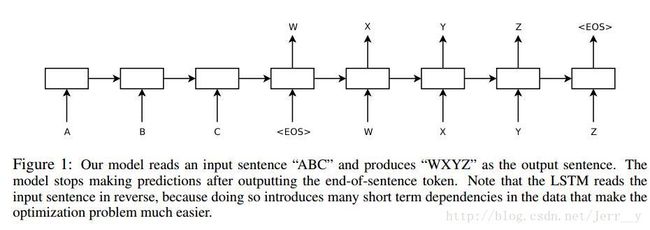
还有一种方式，如上图，我们只需要在输入末尾添加，比如这里有输入序列A B C 。我们将输入序列传入模型后，将其映射为序列W X Y Z 作为输出。

回顾RNN语言模型计算序列$y$的概率$p(y)$：
$$p(y)=p(y_1)p(y_2|y_1)p(y_3|y_{1:2})\cdots p(y_m|y_{1:m-1})=\prod _{k=1}^{m}p(y_k|y_{1:k-1})\text{\hspace{1em}(1)}$$
即我们先生成输出序列第一个单词$y_1$，然后根据$y_1$生成$y_2$，然后根据$y_1,y_2$生成$y_3$,依此类推，这是典型的自回归(Autoregressive model)模型。

自回归模型（英语：Autoregressive model，简称AR模型），是统计上一种处理时间序列的方法，用同一变量例如$x$的之前各期，即$x_1^{t-1}$来预测本期$x_t$的表现，并假设它们为一线性关系。因为这是从线性回归发展而来，不过不用$x$预测$y$，而是用$x$预测$x$(自己)。因此叫做自回归。

——维基百科

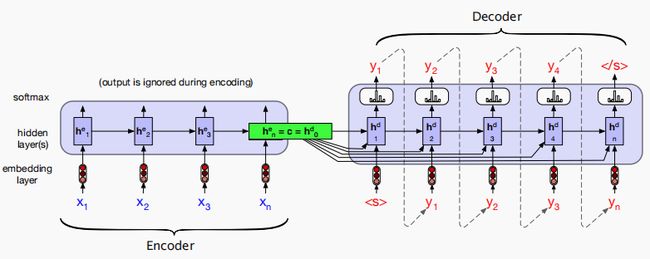
编码器的目标是生成一个输入的上下文表示，体现在编码器最后的那个隐藏状态，$h_n^e$，也用$c$来表示，代表上下文。

在时刻$t$，将前面的$t-1$个单词输入到语言模型，通过前向推理生成隐藏状态序列，并且以最后一个单词的隐藏状态作为起点来生成下一个单词。

$g$为激活函数(tanh或ReLU)，计算时刻$t$的输出和隐藏状态$h_t$的公式为：
$$h_t=g(h_{t-1},x_t)\text{\hspace{1em}(2)}$$

最后，编码器通过特定的函数$q$，将所有时间步的隐藏状态转换为上下文向量$c$：
$$c=q(h_1,\cdots ,h_t)\text{\hspace{1em}(3)}$$
这里实际上是简单地选择$q(h_1,\cdots ,h_t)=h_t$，上下文变量仅仅是输入序列最后时间步的隐状态$h_t$。

而解码器接受$c$作为输入，用于初始化解码器的第一个隐藏状态。即， 第一个解码器RNN单元使用$c$作为初始隐藏状态$h_0^d$，同时结合本身的输入自回归地生成一系列输出，一次输出一个元素，知道输出了结束符或者达到最大长度限制。每个隐藏状态以前一隐藏状态和前一隐藏状态生成的输出作为输入(条件)：
$$h_t^d=g({\hat{y}}_{t-1},h_{t-1}^d)\text{\hspace{1em}(4)}$$

但是，这种方法有一个弱点是，随着输出序列的生成，上下文向量$c$的影响将逐渐减弱。一种常用的解决方法是让解码过程的每个时刻都能看到上下文向量$c$：
$$h_t^d=g({\hat{y}}_{t-1},h_{t-1}^d,c)\text{\hspace{1em}(5)}$$
现在，我们解码器的完整公式，每个解码时间步都可看到上下文。$g$以某种程度上代表RNN，${\hat{y}}_{t-1}$是由上一时刻从softmax生成的输出：
$$\begin{array}{rl}c& =h_n^e\\ h_0^d& =c\\ h_t^d& =g({\hat{y}}_{t-1},h_{t-1}^d,c)\\ z_t& =f(h_t^d)\\ y_t& =\text{softmax}(z_t)\end{array}\text{\hspace{1em}(6)}$$
这里$f$通常为线性层，目的是将$h_t^d$的维度扩大到词表大小，以后面通过softmax计算概率分布。

最后，每个时间步的输出$y$包含词表中每个单词作为预测单词的概率。我们计算每个时间步最可能的输出，通过：
$${\hat{y}}_t=\arg \underset{w\in V}{\max }P(w|x,y_1,\cdots ,y_{t-1})\text{\hspace{1em}(7)}$$

参考

1. Dive Into Deep Learning
2. Speech and Language Processing