自创一个上不了台面的算法题

最近在工作中使用到了一种叫做复杂事件处理 (Complex Event Progressing，CEP) 的技术，来实现关于实时流分析引擎中通过分析事件间的关系，建立不同的事件关系序列库，利用过滤、关联、聚合、模式匹配等技术，最终由简单事件产生高级事件或商业流程。

题目：

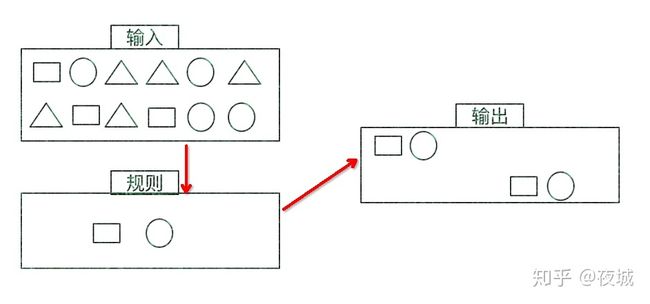
要想把大象装冰箱，总共分几步？

1. 把冰箱门打开 A
2. 把大象装进去 B
3. 把冰箱门关上 C

遇到一个时序的集合，[B, A, D, A, C, D, B, D, A, B, C, B, B, D, C]，D代表与装大象进冰箱无关的类别，那么请问，满足ABC连续或非连续的可能性有多少种？

有愿意尝试或者分享解题思路的小伙伴可以给我留言

从题目上我们很轻易可以看到：

[B, A, D, A, C, D, B, D, A, B, C, B, B, D, C]

[B, A, D, A, C, D, B, D, A, B, C, B, B, D, C]

[B, A, D, A, C, D, B, D, A, B, C, B, B, D, C]

都可以满足要求。这道题一共有

[1, 6, 10]
[1, 6, 14]
[1, 9, 10]
[1, 9, 14]
[1, 11, 14]
[1, 12, 14]
[3, 6, 10]
[3, 6, 14]
[3, 9, 10]
[3, 9, 14]
[3, 11, 14]
[3, 12, 14]
[8, 9, 10]
[8, 9, 14]
[8, 11, 14]
[8, 12, 14]

16 种可能性。

还有很多种情况可以满足，这道题听起来很像动态规划DP。但是并没有很好的状态转移方程。

这道题主要的目的是为了解决在流量安全检测中对于指定的攻击路径进行匹配，例如：

1. 对目标IP进行端口扫描行为
2. 对高危端口进行poc验证
3. 对漏洞进行利用

如果匹配的行为在一个时间段内达到了峰值，那么产生告警并交给安全运营人员做后续处理。

最后我贴一个我的思路

#!/usr/bin/env python
# encoding: utf-8
class Solution(object):

    def buildTwoDimensionArray(self, lst: list, subSet: list) -> [list]:
        rows = len(subSet)
        cols = len(lst)
        ret = [[] for _ in range(rows)]
        for i in range(cols):
            if lst[i] in subSet:
                ret[subSet.index(lst[i])].append(i)
        return ret

    def recursive(self, arr: [list], current_value: int, lst: list): # lst的长度其实是深度
        if len(lst) == len(arr):
            print(lst)
            return
        # 取lst最后一个元素
        last_element = lst[-1] if len(lst) > 0 else None
        if last_element is None or current_value > last_element:
            lst.append(current_value)
            if len(lst) == len(arr):
                self.recursive(arr, current_value, lst)
            else:
                tmp_lst = arr[len(lst)]
                for i in tmp_lst:
                    self.recursive(arr, i, lst)
            lst.pop()