第三课.图变分自编码器&图对抗生成网络

自编码器与变分自编码器

自编码器

自编码器即 Auto Encoders，简称 AE，假设存在一个神经网络：

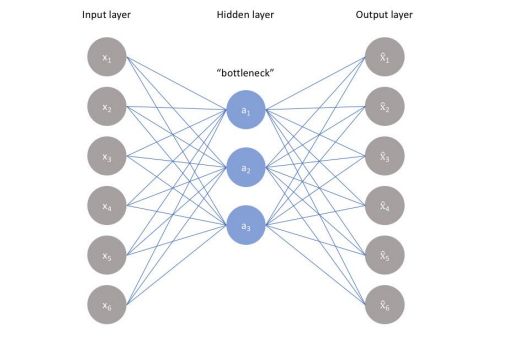
容易发现，该神经网络的输入与输出维度相同，隐藏层的张量维度远小于输入或输出数据，通常目标是用输入还原输出，应使两者相接近，所以有损失函数 $L(x,x)$，参数前者是输入，后者是网络输出；可以看出，自编码器是一种无监督学习，在这种技术中，利用神经网络进行表征学习；

理想的自编码器模型应具备如下性质：

• 对输入足够敏感，能够准确重建数据；
• 模型对输入不够敏感，不能简单地记忆或过拟合训练数据；

通常，将自编码器中生成的最小维度张量称为 Embedding Space 或者 Latent Space：

自编码器是一个包含编码器和解码器的神经网络；编码器以数据点 $X$ 作为输入，并将其转换为低维表达 $Z$；解码器取低维的表达 $Z$，返回一个与输入 $X$ 相似的重构数据 $X$；下图给出了一个以MNIST图像为输入的自编码器的例子：

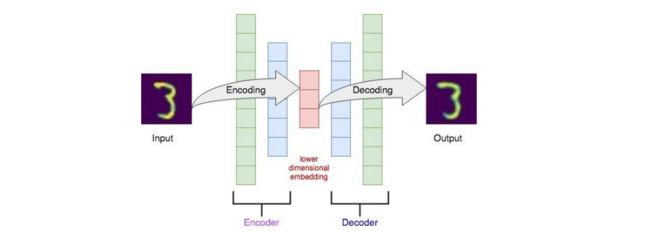
自编码器的损失函数用于衡量重建过程中丢失的信息：
$$L(X,X)=||X-X|{|}^2$$
将高维输入转为低维embedding的意义在于：

• 存储图像的低维嵌入与存储其像素相比，可以节省存储空间；
• 存储图像的低维嵌入也可以节省计算能力，因为输入维数较低；
• 低维数据利于可视化；

低维embedding的可视化举例：

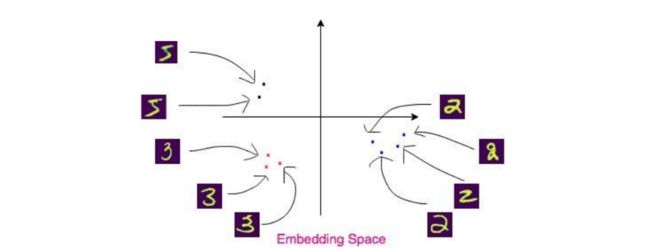
这样，可以直观看出，高维图像各自所属于的分布；对embedding空间的数据进行分类，将会更加方便，提高准确率，提高计算速度

变分自编码器

变分自编码器原理

变分自编码器 Variational Auto Encoders，简称VAE；在传统的 AE 里，只能生成与原始输入相似的图像。然而，VAE 可以从原始数据集中生成新数据；VAE 不需要像 AE 一样让输出数据非常接近输入数据；

VAE 的主要思想是将输入$X$ 嵌入到一个分布而不是一个点上，然后从分布中抽取一个随机样本 $Z$，而不是直接从编码器中产生；VAE 的编码器通常写为 $P(z|x;\phi )$，它取一个数据点 $X$，产生一个分布(多元高斯)，编码器预测高斯分布的均值和标准差；从这个分布中采样低维嵌入 $Z$，解码器为 $P(x|z;\theta )$，它取一个嵌入 $Z$，产生输出 $x$；

---

• 1.生成领域的早期由 AE 与 VAE 主导，当时还没有出现 GAN（对抗生成网络） ；
• 2.$P(z|x;\phi )$ 指在参数为$\phi$的模型下（比如编码器使用全连接神经网络或卷积网络），给定某个输入$x$，生成某个输出$z$的概率；
• 3.$P(x|z;\theta )$指在参数为$\theta$的模型下（比如解码器使用全连接神经网络或卷积网络），给定某个输入$z$，生成某个输出$x$的概率；
• 4.VAE和GAN比较，它们两个的目标基本是一致的——希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。它们是假设了$Z$服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换；

---

变分自编码器可以表示如下：

可见，编码器接收输入数据 $X$，并产生 $\mu$ 和 $log({\sigma }^2)$，注意，如果直接输出 ${\sigma }^2$，必然要求必须为正值，使用对数后，值将映射到正负空间，这有利于帮助网络输出得更轻松；最后，从高斯分布中生成 embedding $Z$，生成的方式为：
$$z=\mu +\sigma \times \epsilon ,\epsilon \sim N(0,1)$$
将 embedding $Z$ 传入解码器（和 AE 的解码器一样），得到一个输出$X$；

变分自编码器的损失函数

变分自编码器的损失函数为：
$$l_i(\theta ,\phi )=-E_{z\sim P(z|x_i;\phi )}[logP(x_i|z;\theta )]+KL(P(z|x_i;\phi )||P(z))$$
VAE 的损失函数分为两部分"变分下界+正则化器"：

• 1.变分下界：用于测量网络重构数据的程度，以防重构数据过度偏离原始数据；
  其中，$z\sim P(z|x_i;\phi )$表示数据$z$采样自一个分布，这个分布服从概率分布$P(z|x_i;\phi )$；
  变分下界计算的是生成输出$x$的概率分布的期望的相反数，生成的$x$越接近原始输入，$P(x_i|z;\theta )$越大（数值在0-1之间），最终变分下界越小；
• 2.正则化器：通过KL散度衡量两个分布，KL散度衡量输出分布$P(z|x_i;\phi )$与隐分布$P(z)$的相似性，两个分布越相似，KL散度越小；
  正则化器的存在约束了编码器输出的分布$P(z|x_i;\phi )$，强迫该分布去接近隐分布$P(z)$，隐分布是人为可定义的，常常使用高斯分布，实际上隐分布也可以采用其他的概率分布；

---

VAE的中“变分”，是因为损失函数的推导过程用到了KL散度及其性质

---

图变分自编码器

定义回顾

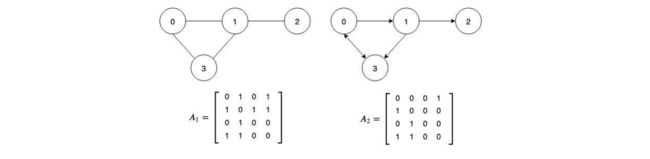
涉及到图数据的处理时，首先回顾邻接矩阵（Adjacency Matrix），邻接矩阵代表图的结构：

• 行$i$和列$j$的值为1表示顶点$i$和顶点$j$之间存在一条边；
• 行$m$和列$n$处的值为0表示顶点$m$和顶点$n$之间没有边；

关于图数据，还要回顾特征矩阵（Feature Matrix），特征矩阵代表图的特征：

• 我们使用特征矩阵$X$来表示输入图中每个节点的特征；
• 特征矩阵$X$的行$i$表示顶点$i$的特征向量；

图变分自编码器

图变分自编码器 Variational Graph Autoencoders，简称 VGAE 或者 GVAE，是用于处理图数据的变分自编码器；VGAE的编码器(推理模型)由图卷积网络( GCN )组成，它以邻接矩阵$A$和特征矩阵$X$作为输入，输出 embedding 空间的变量$Z$：

---

GCN回顾 第二课.图卷积神经网络

---

Encoder

第一个GCN层生成一个低维特征矩阵：
$$\overline{X}=GCN(X,A)=ReLU(AX{W}_0),A=D^{-\frac{1}{2}}(A+\lambda I)D^{-\frac{1}{2}}$$
第二个GCN层生成$\mu$和$log{\sigma }^2$：
$$\mu ,log{\sigma }^2=GC{N}_{\mu ,\sigma }(X,A)=A\overline{X}{W}_1$$
联立一层GCN和二层GCN，可以得到编码器的计算：
$$\mu ,log{\sigma }^2=A[ReLU(AX{W}_0)]W_1$$
然后可以从分布中采样$Z$：
$$z=\mu +\sigma \times \epsilon ,\epsilon \sim N(0,1)$$

Decoder

解码器又称为生成模型，解码器（生成模型）由embedding变量 $Z$ 之间的内积定义；解码器的输出是一个重构的邻接矩阵 $A$，定义为：
$$A=sigmoid(z{z}^T)$$
注释：假设图数据中共$n$个节点，得到隐变量的形状为$z\in {\mathbb{R}}^{n\times \ast }$，$\ast$表示任意维数，经过内积，$A$的形状和邻接矩阵$A$的形状一致，均为$n\times n$；

Decoder使用内积的原因：想寻求一种方法，衡量各个顶点之间的相似性（存在顶点之间的关系信息），从而达到生成一个新邻接矩阵的目标，这个新邻接矩阵包含了节点之间的关系信息，因此是具有意义的

图变分自编码器的损失函数

VGAE 的损失函数和 VAE 的损失函数形式一致：
$$L=-E_{Z\sim P(Z|X,A;W_0,W_1)}[logP(A|Z)]+KL(P(Z|X,A;W_0,W_1)||P(Z))$$
第一项变分下界用于测量网络重构数据的程度，以防重构数据过度偏离原始数据；第二项正则化器约束编码器输出的分布接近人为定义的隐分布$P(Z)$（比如高斯分布）；

图对抗生成网络

对抗生成网络

GAN即Generative Adversarial Network，GAN由两部分组成，一个是生成器Generator，另一个是判别器Discriminator，GAN 的内容回顾 Pytorch笔记本-第十课.图片风格迁移和GAN；GAN 广泛用于图像生成和语音生成：

一般游戏开发和动画制作费用昂贵，往往需要雇佣许多艺术家从事相对常规的工作，通过GAN就能快速且低成本生成动画人物：

通过额外的姿态输入，也可以将图像转换为不同的姿态（多用于电商行业）：

图对抗生成网络 GraphGAN

图对抗生成网络即 GraphGAN，由一个Generator和Discriminator组成；关于GraphGAN，需要注意以下符号说明：

• $Graph$：图数据 $Graph(V,E)$；
• $V$：节点集合；$v_c$：当前节点；$N(v_c)$：当前节点的一阶邻居（与$v_c$有边直接相连的节点）；
• $E$：边集合；
• 生成器模型$G(v|v_c;{\theta }_G)$尽可能拟合出真实数据的分布$p_{true}(v|v_c)$，$G(v|v_c;{\theta }_G)$反映了在参数为${\theta }_G$的模型下，预测出节点集合中的某个任意节点$v$与当前节点$v_c$有边连接的概率；
• 判别器模型$D(v,v_c;{\theta }_D)$用于判断哪些边连接正确，哪些边连接错误，即预测一对顶点之间存在边的概率$p(edge|(v_i,v_j))$；

GraphGAN的训练过程如下：

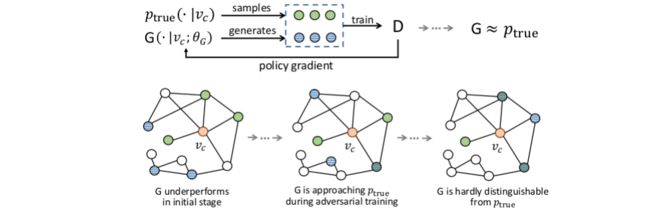
训练方式其实与GAN是一样的，也是交替训练，最开始固定生成器，训练判别器，再固定判别器，训练生成器，以此交替训练；

训练的目标：
$$mi{n}_{\left\{{\theta }_G\right\}}ma{x}_{\left\{{\theta }_D\right\}}V(G,D)$$
其中：
$$V(G,D)=\sum _{c=1}^V(E_{v\sim p_{true}(v|v_c)}[logD(v,v_c;{\theta }_D)])+(E_{v\sim G(v|v_c;{\theta }_G)}[log(1-D(v,v_c;{\theta }_D))])$$
可看出，先对于${\theta }_D$最大化$V(G,D)$，即固定$G$，训练$D$；再对于${\theta }_G$最小化$V(G,D)$，即固定$D$，训练$G$