机器学习：简单的支持向量机

1.线性可分支持向量与硬间隔最大化

1.1线性可分

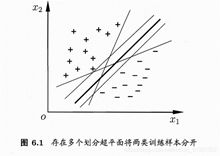
由上图6.1所示的两个类 + 和 - ,在二维空间中很容易在图中画出一条直线将两组数据点分开，在这种情况下，这组数据被称为线性可分。但是在许多实际情况中，数据点是多维的，所以下面引入超平面

1.2超平面的理解与表达

在数学中，超平面是n维欧氏空间中，余维度为1的子空间[1]。即超平面是n维空间中的n-1维的子空间。它是平面中的直线、空间中的平面推广。

0维的点可以将1维的线分为两个部分

1维的线可以将2维的平面分成两个部分

2维的面可以将3维的体分成两部分

以此类推，n-1维的子空间，可以将n维的空间分为两个部分。所以超平面就是这个n-1维子空间，他就像3维空间中的平面，可以用来将n维空间分割成为两个部分

超平面的表示方法推导：
任意维度表示方法都有： W(X-Xo)=0（这里的W X可为多维）
有 wx-wx_0=0 令 wx_0 为常数b
得到超平面表达方法 wx-b=0

其中 W=(w_1: w_2:…: w_n)为法向量（方向与超平面方向垂直），决定超平面的方向，b为移项，决定了超平面与原点之间的距离。

显然划分超平面可被法向量W和位移b确定

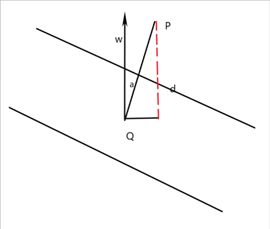
我们将其记为(w,b)有样本空间中任意点X到超平面的距离可写为 γ=|w^T x+b|/‖w‖
下面推导该距离公式

1.3空间中的点到超平面的距离

1.4间隔大小

有许多条线可以分割两组不同的数据 如果用较粗的线来画则会有所不同 如下图：

可以发现有且仅有一条线，满足正确分割两组数，据稍微旋转都会导致部分点分类错误 如下图：

则认为灰色中间的那条线即为最佳曲线，应为改超平面对训练样本局部扰动的“容忍性”最好，保证这种情况下训练集外的样本离两个类的分隔界最远，其泛化能力最强。Margin即为间隔大小 如下图：

间隔得推导如下：

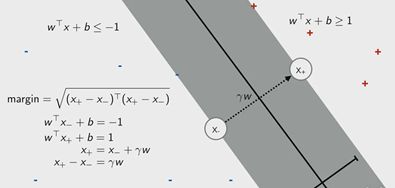
1.5最小间隔数据点与间隔最大化

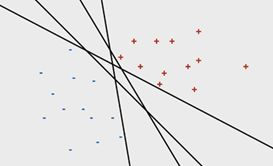
在改划分中，不同的(w,b)代表不同的直线，在不同的直线中，距离直线最近的那些点称为最小间隔数据点，在直线两侧的最小间隔数据点到该直线的几何距离之和，称为间隔
Ps:认识函数距离和几何距离

函数距离即类似为y1 ，y2，两个平行直线之间的距离，几何距离即点到直线的距离

函数距离和几何距离的关系为

其中yi 为几何距离 y ̂ i 为函数距离
（可类比点到直线的距离理解）

现根据最优解直线定义求解最优解 即在不同的最小化的，数据点的间隔中寻找最大间隔的直线，该直线的(w,b)即为最优解

其中最大化2/‖w‖ 与最大化‖w‖结果相同
再转化为1/2 ‖w‖^2方便求导，故最后的目标和约束条件如下图所示

2.学习的对偶算法

2.1拉格朗日对偶性

2.1.1原始问题

引入拉格朗日函数解决原始问题

2.1.2对偶问题

初学阶段只理解了这是一个求优化最优解的方法，通过将问题转化解决问题

2.2求解对偶问题得到线性可分最优解

通过对偶算法，将问题转化为

接下来就是求出这些alpha,一旦这些alpha被求出来，便马上可以表达出超平面，SVM的主要工作就是求解这些alpha.

带入超平面表达方式wx+b=0为

再通过分类决策函数（参数值>0函数值为1，参数值<0函数值为-1）

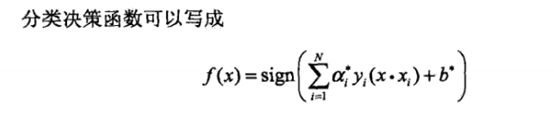
3.线性支持向量机与软间隔最大化

3.1引入松弛变量

线性可分问题的支持向量机学习方法对线性不可分训练数据不适用，所以要对最大化间隔进行修改，让其对特异点的数据有所惩罚，可包容部分特异点，即将“硬间隔”变为“软间隔”



最后问题转化为

4.非线性支持向量机与核函数

4.1核技巧与核函数

当数据集为线性不可分时，此时的软间隔也将不起作用，此时可用核技巧来解决问题
当数据为线性不可分时，可转变空间维度，将数据变为线性可分。


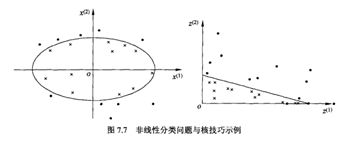
这里类似于换元技巧 将x^2+y ^2=n（n为常数）换元为i+j=n（n为常数）转变空间维度简化为线性问题。
故线性求解非线性为两部：
①使用函数变换，将原空间数据映射到新空间转变为线性问题
②如开始求解线性问题一般训练数据分类模型求解非线性问题
核函数定义：

4.2核技巧在支持向量中的应用

将核技巧应用于对偶问题的目标函数中的内积xi⋅xj换为特征空间中的Φ(xi )⋅Φ(xj )，该学习时在隐式的特定空间中进行，无需显示定义特定空间和映射函数，只关注内积的值的大小即可，此为核技巧。
故将原对偶问题目标转化为

下面给出几种常用的核函数：

Ps:局部加权线性回归中常用高斯核来对附近点赋予更高权重，随后自定义σ参数大小来设置较远点的惩罚度σ越小，惩罚度越大，附近点权重越高，反之惩罚度越小，附近点权重越小

5.序列最小优化(SMO)算法

5.1算法基本思路

每次循环选择两个alpha进行优化处理，一旦找到一对合适的alpha,那么就增大其中一个的同时减小另一个，合适的alpha条件①这两个alpha必须要在间隔边界之外②这两个alpha还没有经过去区间化处理或者不在边界上。

5.2简化的SMO

下面展示一些 简化的SMO

简化版的SMO跳过了：
外循环中确定要优化的最佳alpha对
忽略了求得 η=0的不常见的情况
了解简化的SMO来初步了解算法思想

import random
from os import listdir
from numpy import mat, shape, zeros, multiply, nonzero, sign
# 加载数据
def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])#将两个元素添加为一个列表 使dataMat为列表的列表
        labelMat.append(float(lineArr[2]))
return dataMat, labelMat

数据样式为如下：

# 随机选择不同数
def selectJrand(i, m):
    j = i
    while j == i:
        j = int(random.uniform(0, m))
    return j
# 用于调整大于H或小于L的alpha值
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj
# 简化的SMO算法
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    b = 0
    m, n = shape(dataMatrix)
    alphas = mat(zeros((m, 1)))#创建0的alphas列表
    iter = 0  #控制要在优化范围内alpha保持不变的迭代次数
    while iter < maxIter:
        alphsPairsChanged = 0
        for i in range(m):#for循环中迭代m次， m为样本训练集的数量
            fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            Ei = fXi - float(labelMat[i])
 
        #Ei为计算误差，如果误差很大便可以对该数据实例alpha进行优化
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
            #toler为函数参数中自主控制的容错率 判断所选中的alpha是否有较大幅度改变，若有，进入if语句开始优化alpha，若没有进入下一轮for循环
                j = selectJrand(i, m)
          #利用selectJrand函数随机选取另一个非i的alpha下标j
                fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b                #计算aj 的g(x)
                Ej = fXj - float(labelMat[j])
                   #计算误差
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                       #复制两个所选中的alpha值，便于比较新值与旧值的变化
                if labelMat[i] != labelMat[j]:
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print('L == H')
                    continue
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - \
                     
                     #eta所求即为-η 可知一般情况下eta<0
                     #极少数情况出现eta=0 这里为简化的SMO故不考虑
                      dataMatrix[j, :] * dataMatrix[j, :].T
                if eta >= 0:当eta>=0#求解失败，需要退出for,循环
                    print("eta == 0")
                    continue
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
 #可直接求出a2
                alphas[j] = clipAlpha(alphas[j], H, L)
 
#利用clipAlpha函数来完成上述步骤 截取a_2的值
                if abs(alphas[j] - alphaJold) < 0.00001:
                    #检查a2 是否有较大改变，不是就退出该层次for循环
                    print("j not moving enough")
                    continue
                    
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
 #求的有效的a2^new带入公式求a1^new
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * \
                     (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * \
                     (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
 
 
          #利用公式求得b_1^new  b_2^new
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2)/2.0
 
                alphsPairsChanged += 1
         #程序执行到此已经成功的改变了一对alpha，故alphsPairsChanged+1
                print("iter: %d i: %d, paris changed %d" % (iter, i, alphsPairsChanged))
        if alphsPairsChanged == 0:
            iter += 1
 #若alphsPairsChanged==0则alpha没有发生改变，iter+1,认为成功完成一次while循环
        else:
            iter = 0

        print("iteration number: %d" % iter)
return b, alphas

fXi为计算g(x)的值

Ei为计算误差，如果误差很大便可以对该数据实例alpha进行优化

eta所求即为-η 可知一般情况下eta<0，极少数情况出现eta=0 这里为简化的SMO故不考虑

可直接求出a2

利用clipAlpha函数来完成上述步骤 截取a2的值

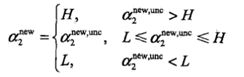
求的有效的a2^new
带入公式求a1^new

利用公式求得：
b_1^new
b_2^new

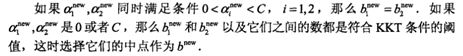
若alphsPairsChanged != 0 则alpha发生了改变，表明此时的alpha还未收敛到最优的alpha集，故令iter=0来重置while循环使其继续收敛（即方才不算作进行了一次while循环），只有alpha的值不改变，inter递增1才算作进行了一次while，并且只有持续如此直到alpha值maxIter次循环都不发生改变(即已找到最佳alpha集，已收敛)，才会退出循环，此时即得到最优的b, alphas