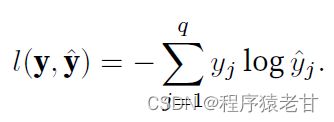基于Pycharm运行李沐老师的深度学习课程代码

最近在b站看李沐老师的深度学习课程，受益颇多。不过觉得光看视频实在是不过瘾，最好还是能实际的玩起来。鉴于我还是习惯使用pycharm，且不需要过多的中间过程展示，所以代码的编写基本都是在pycharm进行。由于李沐老师的代码主要是在Jupyter运行的，在pycharm上使用会略有差异。本篇博客以求解线性优化问题代码为例，来谈一谈在pycharm运行相关代码的一些注意事项。

教程网站：Dive into Deep Learning — Dive into Deep Learning 1.0.0-alpha0 documentation

中文网站：《动手学深度学习》 — 动手学深度学习 2.0.0-beta1 documentation

---

一. 安装d2l

除了安装常用的pytorch和torchvision等包以外，在运行相关代码时，会看到使用d2l包调用一些包装好的代码，如下：

import random
import torch
import numpy
from d2l import torch as d2l

这个d2l在pycharm里搜索可能搜不到。我在查阅网上其他人的介绍，通常是在Anaconda的环境中使用pip install来安装。首先我们打开anaconda虚拟环境，激活当前环境，并运行pip install d2l来运行包的安装，步骤如下：

1）使用conda info --envs列出所有的虚拟环境

2）找到你项目所在的虚拟环境，激活：activate your_envs_path

3）pip install d2l

在安装完d2l后，这时我们就可以运行代码了。

---

二. 结果显示

和Jupyter不同的是，在pycharm中我们不能直接使用变量名来查看数据，一般都要附加对应的打印或者显示程序才能看到对应的结果，如下：

import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y

在Jupyter中，结果就被直接显示出来了，但是在pycharm中，需要打印：

print(x+y,x*y,x/y,x**y)

同理，图像显示也需要使用相应的显示代码：

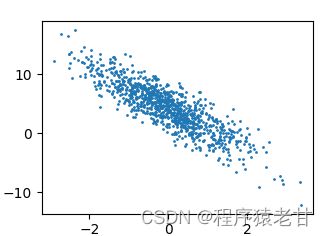
d2l.set_figsize()
d2l.plt.scatter(f,l,1)
d2l.plt.show()

显示结果：

---

三. 代码实例

下面，我们把pycharm中验证过的完整的线性优化代码列出来，以供参考：

import random
import torch
from d2l import torch as d2l

def synthetic_data(w,b,num_examples):
    X = torch.normal(0,1,(num_examples,len(w)))
    y = torch.matmul(X,w)+b
    y += torch.normal(0, 0.1, y.shape)
    return X,y.reshape((-1,1))

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
# 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

def linreg(X, w ,b):
    return torch.matmul(X ,w) + b

def squared_loss(y_hat, y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

def sgd(params, lr, batch_size):
    with torch.no_grad():
        for param in params:
            param -= lr*param.grad / batch_size
            param.grad.zero_()

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:', features[0],'\nlabel:', labels[0])

a = torch.ones(3)
b = a.numpy()
f = features[:,1].numpy()
l = labels.numpy()

d2l.set_figsize()
d2l.plt.scatter(f,l,1)
d2l.plt.show()

batch_size = 10

#for X, y in data_iter(batch_size, features, labels):
#    print(X, '\n', y)

w = torch.normal(0., 0.01, size = (2,1), requires_grad= True)
b = torch.zeros(1 , requires_grad = True)
lr = 0.03
num_epochs = 10
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
           l = loss(net(X, w, b), y) # X和y的⼩批量损失
           # 因为l形状是(batch_size,1)，⽽不是⼀个标量。l中的所有元素被加到⼀起，
        # 并以此计算关于[w,b]的梯度
           l.sum().backward()
           sgd([w, b], lr, batch_size)
    with torch.no_grad():#是一个上下文管理器，被该语句 wrap 起来的部分将不会track梯度
           train_l = loss(net(features, w, b), labels)
           print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

如果未来发现一些新的问题，我会持续更新该博文。

---

2022/8/24 更新：

在学习了softmax部分内容后，我发现有一些需要注意的点，首先：

softmax章节里关于Fashion-MNIST数据集可视化的代码:

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save
     figsize = (num_cols * scale, num_rows * scale)
     _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
     axes = axes.flatten()
     for i, (ax, img) in enumerate(zip(axes, imgs)):
         if torch.is_tensor(img):
              ax.imshow(img.numpy())
         else:
              ax.imshow(img)
         ax.axes.get_xaxis().set_visible(False)
         ax.axes.get_yaxis().set_visible(False)
         if titles:
              ax.set_title(titles[i])
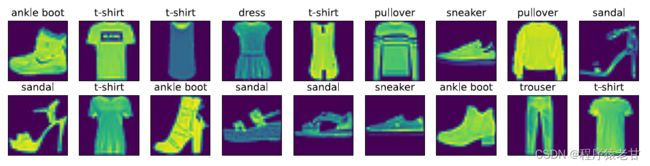
     d2l.plt.show()
     return axes

之前已经介绍过，要在最后添加：d2l.plt.show()。结果如下：

另外，注意下面代码： 

y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

这段代码其实要注意最后一句，y_hat[[0, 1], y]意思是以tensor y内部的内容作为索引号，对y_bat内部的元素0和1提取对应索引的值。y的第一个元素为0，进而提取y_hat第0个元素内的第0个索引值，即0.1。因此输出的结果为tensor([0.1000, 0.5000])。在定义网络结构和交叉熵的时候，作者的代码写的很巧妙，以至于不太直观，如下：

def net(X):
     return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

def cross_entropy(y_hat, y):
     return - torch.log(y_hat[range(len(y_hat)), y])

X.resahpe((-1, W.shape[0]))即按照图片的顺序，将X按照每一幅图拉成一个一维向量。-1表示的是缺损值。假设全部数据是L = [18,1,28,28], 18是一个batchsize的尺寸。W.shape[0]表示18，即数据集的尺寸，那么reshape就是(L/18, 18)。这里是为了乘以W(18, 40)而做的转置。而在交叉熵函数中，y_hat[range(len(y_hat)), y]，如提到的，就是按照y的索引，来提取y_hat每一个元素对应索引位置的值，即softmax的最大概率值，即实现公式：