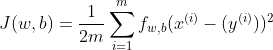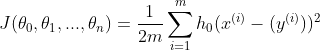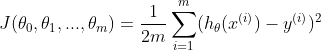吴恩达机器学习笔记——Day1

观看的视频来自网易云课堂——《吴恩达机器学习》
http://吴恩达机器学习 - 网易云课堂 https://study.163.com/course/courseMain.htm?courseId=1210076550

 模型 （model）：  其为预测值 

 参数 （parameters）：w，b

 代价函数  ：

        其中 J(w,b)要尽可能地小从而保证代价最少

 目标 （goal）：mimimize J(w,b)

梯度下降原则：梯度下降就是找到一个 值并期望其可以将代价函数最小化

 : learning rate 学习速率     ,可以看作控制向局部最低点靠近时走的步数

求导部分代表向局部最低点靠近时选择的方向

对于分级下降算法，需同时更新 w 和 b (simultaneously update w and b)，重复计算 w 和 b 直到代价函数收敛(repeat until convergence)

当靠近局部最低点时，梯度下降会根据梯度下降原则自动变换为较小的幅度，因此，即使再学习速率保持不变时，梯度下降也可以收敛到局部最低点，这就是梯度下降的做法。

若梯度下降算法正常工作，每一步迭代后的代价函数值都应下降，当代价函数不再下降则说明其已经收敛。

建议在计算的同时画一条以迭代次数为横坐标，代价函数值为纵坐标的图像以观察其收敛情况。若图像刚开始就呈现上升趋势或上升下降反复波动，可能使由于学习率过大。针对线性回归，只要学习率足够小，每次迭代后的代价函数都会下降，但过小的话则会导致梯度下降算法收敛很慢

常用值：...、0.003、0.001、0.03、0.01、0.3、0.1、1、...

线性回归算法

多元线性回归：通过多个特征量或变量来预测   

模型 （model）：

参数 （parameters）：

代价函数：

梯度下降：

注意：要反复重复这个过程,变换j的值。

特征缩放

        将有多个特征值  的取值保持在相近的范围内，进而时梯度下降法可以更快达到收敛。默认规定， 的值等于1 

        有较多的特征值会使在寻找最小代价的路上发生反复偏移、来回振荡，进而导致寻找最佳路径的过程耗时增加，通过特征缩放可以使其范围变得相近。

特征缩放法：（不用太精确，只为达到提高运行效率的目的）

1、特征值除以最大值：使特征值可以约束在一定范围之间，范围不要过大也不要过小，如[-1，1]、[2，3]，从而使代价函数更快收敛。

2、均值归一化：利用  代替  使特征值具有为0的平均值，但其方法不应用于（默认=1）

特征：通过定义新的特征，得到更好的模型

将已知的特征值进行数学变换得到新的更能描绘数据得特征值

多项式回归：将一个多项式拟合到数据上

将多元线性方程拟合，从而使其代价函数值可以趋向于某一个值

  或   

正规方程：提供了一种代替迭代法求  的解析方法

 ,       

对于    ,  使  , 得到的  就可以得到代价函数的最值。

假设有m个训练样本，有n个特征值，对于每一个训练样本都有n+1维特征向量。

做法：在  前还有恒等为1的  ，构建一个矩阵x包含训练样本中所有的特征变量x，，其为m*(n+1)维矩阵，对输出y也进行向量表示，其为m维向量。

从而可以计算得到使得代价函数最小化的。

正规方程计算可以不用特征缩放，但是梯度下降法，特征缩放很重要。

梯度下降法（适合多约>10000）	正规算法（适合少）
需要选择学习率，这就代表要运行多次	不需要选择学习率
需要更多次的迭代，耗时长，但特征变量多也可以运行很好	不需要迭代。特征量多会带来很大的计算量，耗时很慢，将是维数的三次方

对于不可逆矩阵情况很少发生，即使矩阵不可逆，也可使用软件Octave中的pinv函数计算。