算法与数据结构（第二周）——排序基础：插入排序法

目录

插入排序

插入排序简单介绍

实现插入排序法

插入排序法的一个小优化

插入排序法的特性

---

插入排序

        插入法排序的思路就是将要排序的数组分两个区间，一个是已排序区间，一个是未排序区间。初始时，默认第一个元素是已排序区间的，后面的所有元素为未排序区间。然后依次取未排序区间的元素，在已排序区间找到合适的位置插入，直到排完所有数据。

插入排序简单介绍

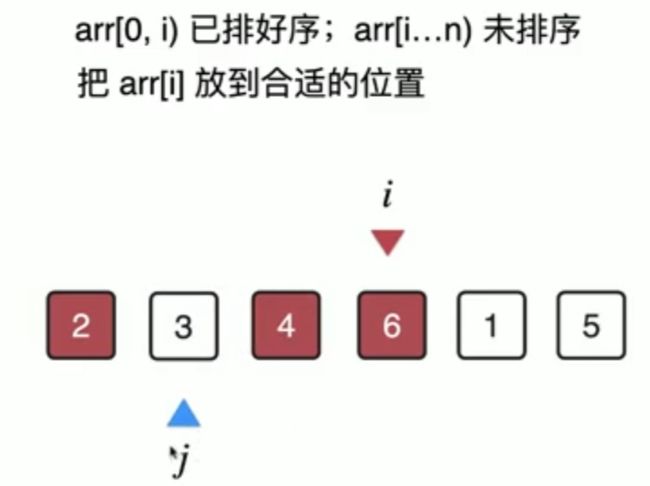
        插入排序法每次处理一个元素，我们设置一个索引i来指向当前我们所处理的这个元素，初始的时候，这个索引i指向第一个元素，对于arr数组来讲，从0到i已排好序，从i到n未排序，从i=0开始，每次只处理一个元素，把arr[i]放到合适的位置。

        当i等于0的时候，我们处理第一个元素，第一个元素6。自己所在的位置，不需要插入到任何位置，前面也没有任何元素，所以就放在那里即可。此时i++，i指向4，这个时候我们就需要考虑一下四是否需要插入到前面某一个位置，为了判断4这个元素能否插入前面的某个位置，我们引入j，这个j初始指向4所得的位置，然后看前面的元素是6，比4大，那么四应该插入到六前面，于是将4和6交换下位置，交换位置之后，相应的这个j就跟着4来到了索引为0的位置。当来到索引为0的位置，j前面就没有索引了，四不可以再向前插入了，所以我们知道四就应该放在当前这个位置了。

         i++，我们来看下一个元素，也就是2这个元素，我们来看二是否需要插入到前面的某个位置，于是j先指着2的位置开始，先看j-1的位置，2比6还要小，因此需要互换位置。

        因此2来到了索引为1的位置，那么此时还没有结束。我们还要看2所在的位置是否还需要插入到前面的元素，我们发现4比2还要大，因此还要互换位置。此时j已经等于0了，不可能再插入到前面了，所以我们知道2已经来到了他所在的位置。

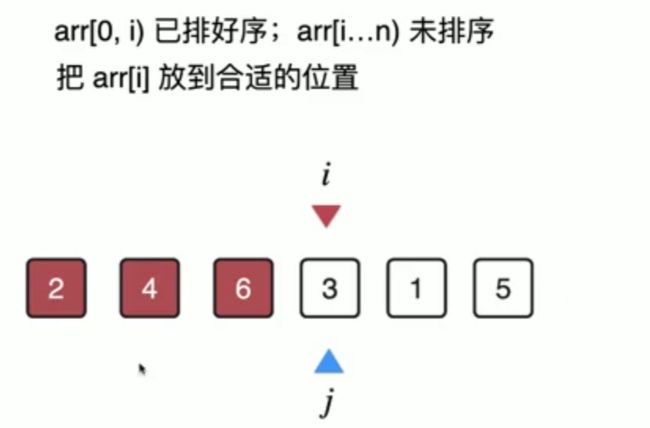
        此时i++，我们来看下一个元素，我们使用索引j来指向3这个元素，我们再看第j-1个元素，6比3大，因此需要互换位置。

        此时仍需要和第j-1个元素相比，可以看到4比3大，所以仍需要互换位置。

        我们继续来看3这个元素是否还能往前插入，我们发现前面一个元素二是比三小的，所以三这个元素已经来到了一个正确的位置，此时我们已经处理好了3这个元素。

        对于插入排序法来说，每次只处理当前的元素，把当前元素放到合适的位置。所以插入排序法永远不会动i还没有便历到的位置。

实现插入排序法

public class InsertSort {
    private InsertSort() {
    }
    public static > void sort(E[] arr){
        for (int i = 0; i < arr.length; i++) {
            //将arr[i]插入到合适的位置   j - 1 >=0 保证前面的元素存在
            for (int j = i; j - 1 >=0; j--) {
                if (arr[j].compareTo(arr[j-1])<0){
                    swap(arr,j,j-1);
                }else break;//如果不是的话就不需要交换位置了
            }
/*
            for (int j = i; j - 1 >=0 && arr[j].compareTo(arr[j-1])<0; j--)
                swap(arr,j,j-1);
*/

        }
    }

    private static  void swap(E[] arr, int i, int j) {
        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    public static void main(String[] args) {
        int[] dataSize = {10000,100000};
        for (int n:dataSize){
            Integer[] arr = ArrayGenerator.generateRandomArray(n,n);
            SortingHelper.sortTest("InsertSort", arr);
        }
    }

}

插入排序法的一个小优化

        我们之前所使用的逻辑是使用j来指向三所在的位置，并不断的和前面的元素相比较大小，然后6比3大则交换位置，4比3大则继续交换位置，位置2不比3大，所以位置不再交换。

        三来到正确的位置之后，其后面的四和六只是做了一个平移，这个便宜的过程其实只需要靠一次赋值就可以完成，最终我们知道三应该放在索引为1的位置，我们再把3这个元素赋值在这里就行。

初始化：

        我们先使用一个变量暂存下3，具体处理的时候，我们依然看j前面的一个元素，前一个位置的元素6，6比3还要大，下面要做的事情是直接让arr[j]等于6就好了，注意，这只是一个赋值操作，也就是六往后平移一个位置，然后j--。

        我们继续判断三是否应该放在索引为二的位置，也就是当前这个位置，此时需要和第j-1位相比较，经过比较的4比3要大，所以让arr[j]等于4，然后j--。

        我们继续判断三是否放在索引为1的位置，也就是当前j的位置，此时需要和第j-1位相比较，经过比较的2比3要小，所以3应该插入到j的位置，此时只需要arr[j]＝暂存的3即可。

        在前面的操作中，我们只用了一次赋值，而不是一次交换，每一次交换都需要三步操作，但是每一次赋值只是一次操作，这样一来，我们对我们的插入排序法行了一个小的优化，不过这个优化不是一个时间复杂度的优化，我们即使这样写之后插入排序法依然是一个O(n^2)的算法。

    public static > void sort2(E[] arr){
        for (int i = 0; i < arr.length; i++) {
            //将arr[i]插入到合适的位置
            //先暂存arr[i]这个元素
            E t = arr[i];
            // 然后再通过j找到该元素实际存放位置
            int j;
            for (j = i; j - 1 >= 0 && t.compareTo(arr[j-1])<0; j--) {
                arr[j] = arr[j-1];//元素向后平移
            }
            //将t放在arr[j]当中
            arr[j] = t;
        }
    }

插入排序法的特性

        对于插入排序法，他存在一个内层循环提前终止的机制，这种机制会使得在很多情况下，我们这个内层循环不一定要遍历到从i到1这么多轮儿，在最极端的情况下，如果排序的这个数组本身已经是有序的，在这种情况下插入算法的运行过程是什么样子的呢？

        i从零开始，那么刚开始处理一个元素，第一个元素不需要插入，那么第一个元素就直接处理完了，然后i++，以后指向第二个元素，第二个元素是二，我们开始寻找第二个元素，这个二它插入的位置往前看一个元素，往前看一个元素，我发现一直接就小于二，那么说明这个位置本身就是我们这个第二个元素二需要待在的位置，那么这个二呢就直接放在这儿了，这样我们第二个元素也就处理完了，直接i加加加加之后我们要处理三这个元素，我们来找三这个元素，它需要插入的位置在哪里？烟是我们直接向前看一步看到三，前面的元素是二，那么对于二这个元素来说，它已经小于三了，说明这个位置本身就是三这个元素一带的位置，那么我们就直接找到了三这个元素就放在这个位置，它就处理完了，然后继续i++，以此类推。

          如果我们初始的数组它本身已经是有序的,我们的内层循环其实每一次只是看了一下前面那个元素发现前面那个元素就是比它自身小，就说明了我们当前这个元素就应该待在这儿，然后那一重循环就结束了，换句话说，每一次我们内层循环只执行了常数级别的操作，那么在这种情况下对于一个有序数组来说，我们的插入排序算法它的时间复杂度就变成了O（n）这个级别。

在n为10000和100000的情况下选择排序法和插入排序法的对比：