机器学习多元线性回归

Linear regression is useful when we want to predict the values of a variable from its relationship with other variables. There are two different types of linear regression models (simple linear regression and multiple linear regression).

当我们想根据变量与其他变量的关系预测变量的值时，线性回归很有用。有两种不同类型的线性回归模型(简单线性回归和多重线性回归)。

In predicting the price of a home, one factor to consider is the size of the home. The relationship between those two variables, price and size, is important, but there are other variables that factor in to pricing a home: location, quality, location, parking, and much more. When making predictions for price (dependent variable), we’ll want to use multiple independent variables. To do this, we’ll use Multiple Linear Regression.

在预测房屋价格时，要考虑的因素之一是房屋的大小。价格和大小这两个变量之间的关系很重要，但是还有其他一些变量会影响房屋的定价：位置，质量，位置，停车位等等。在预测价格( 因变量)时 ，我们将要使用多个自变量 。为此，我们将使用多元线性回归。

Multiple Linear Regression uses two or more independent variables to predict the values of the dependent variable. It is based on the following equation:

多元线性回归使用两个或多个自变量来预测因变量的值。它基于以下方程式：

y = b + m_{1}x_{1} + m_{2}x_{2} + ... + m_{n}x_{n}y=b+m1x1+m2x2+...+mnxn

易街 (StreetEasy)

StreetEasy is New York City’s leading real estate marketplace from studios to high-rises, Brooklyn Heights to Harlem.

从工作室到高层建筑，从布鲁克林高地到哈林， StreetEasy是纽约市领先的房地产市场。

In this article, you will be seeing a dataset that contains a sample of 5,000 rentals listings in Manhattan, Brooklyn, and Queens, active on StreetEasy as of June 2016.

在本文中，您将看到一个数据集，其中包含截至2016年6月在StreetEasy上活跃的Manhattan ， Brooklyn和Queens的5,000个出租列表。

It has the following columns:

它包含以下列：

rental_id: rental ID
rental_id ：租金ID
rent: price of rent in dollars
rent ：美元rent价格
bedrooms: number of bedrooms
bedrooms ： bedrooms数
bathrooms: number of bathrooms
bathrooms ： bathrooms数量
size_sqft: size in square feet
size_sqft ：以平方英尺为单位的大小
min_to_subway: distance from subway station in minutes
min_to_subway ：距地铁站的距离，以分钟为单位
floor: floor number
floor ：楼层号
building_age_yrs: building’s age in years
building_age_yrs ：建筑物的年限
no_fee: does it have a broker fee? (0 for fee, 1 for no fee)
no_fee ：它收取经纪人费用吗？ (费用为0，免费为1)
has_roofdeck: does it have a roof deck? (0 for no, 1 for yes)
has_roofdeck ：它有屋顶甲板吗？ (0表示否，1表示是)
has_washer_dryer: does it have washer/dryer in unit? (0/1)
has_washer_dryer ：是否在单元中装有洗衣机/烘干机？ (0/1)
has_doorman: does it have a doorman? (0/1)
has_doorman ：有门卫吗？ (0/1)
has_elevator: does it have an elevator? (0/1)
has_elevator ：有电梯吗？ (0/1)
has_dishwasher: does it have a dishwasher (0/1)
has_dishwasher ：是否有洗碗机(0/1)
has_patio: does it have a patio? (0/1)
has_patio ：有露台吗？ (0/1)
has_gym: does the building have a gym? (0/1)
has_gym ：大楼有健身房吗？ (0/1)
neighborhood: (ex: Greenpoint)
neighborhood ：(例如：Greenpoint)
borough: (ex: Brooklyn)
borough ：(例如：布鲁克林)

Performing Multiple linear regression on the dataset. That contains information about apartments in New York. 对数据集执行多元线性回归。其中包含有关纽约公寓的信息。

训练集与测试集 (Training Set vs. Test Set)

As with most machine learning algorithms, we have to split our dataset into:

与大多数机器学习算法一样，我们必须将数据集划分为：

Training set: the data used to fit the model
训练集 ：用于拟合模型的数据
Test set: the data partitioned away at the very start of the experiment (to provide an unbiased evaluation of the model)
测试集 ：在实验开始时就将数据分割开(以提供对模型的公正评估)

In general, putting 80% of your data in the training set and 20% of your data in the test set is a good place to start.

通常，将80％的数据放入训练集中，将20％的数据放入测试集中是一个不错的起点。

Suppose you have some values in x and some values in y:

假设您在x有一些值，在y有一些值：

from sklearn.model_selection import train_test_splitx_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, test_size=0.2)

Here are the parameters:

以下是参数：

train_size: the proportion of the dataset to include in the train split (between 0.0 and 1.0)
train_size ：要包括在火车分割中的数据集的比例(介于0.0和1.0之间)
test_size: the proportion of the dataset to include in the test split (between 0.0 and 1.0)
test_size ：要包含在测试拆分中的数据集的比例(介于0.0和1.0之间)
random_state: the seed used by the random number generator [optional]
random_state ：随机数生成器使用的种子[可选]

多元线性回归：Scikit-Learn (Multiple Linear Regression: Scikit-Learn)

Now we have the training set and the test set, let’s use scikit-learn to build the linear regression model!

现在我们有了训练集和测试集，让我们使用scikit-learn构建线性回归模型！

The steps for multiple linear regression in scikit-learn are identical to the steps for simple linear regression. Just like simple linear regression, we need to import LinearRegression from the linear_model module:

scikit-learn中的多元线性回归步骤与简单线性回归步骤相同。就像简单的线性回归一样，我们需要从linear_model模块导入LinearRegression ：

from sklearn.linear_model import LinearRegression

Then, create a LinearRegression model, and then fit it to your x_train and y_train data:

然后，创建一个LinearRegression模型，然后将其拟合到您的x_train和y_train数据：

mlr = LinearRegression()mlr.fit(x_train, y_train) 
# finds the coefficients and the intercept value

We can also use the .predict() function to pass in x-values. It returns the y-values that this plane would predict:

我们还可以使用.predict()函数来传递x值。它返回该平面将预测的y值：

y_predicted = mlr.predict(x_test)
# takes values calculated by `.fit()` and the `x` values, plugs them into the multiple linear regression equation, and calculates the predicted y values.

We will start by using two of these columns to teach you how to predict the values of the dependent variable, prices.

我们将首先使用其中两列来教您如何预测因变量价格。

使用Matplotlib可视化结果 (Visualizing Results with Matplotlib)

You’ve performed Multiple Linear Regression, and you also have the predictions in y_predict. However, we don’t have insight into the data, yet. In this exercise, you’ll create a 2D scatterplot to see how the independent variables impact prices.

您已经执行了多元线性回归，并且在y_predict也有了预测。但是，我们还没有洞察数据。在本练习中，您将创建一个2D散点图，以查看自变量如何影响价格。

How do you create 2D graphs?

如何创建2D图形？

Graphs can be created using Matplotlib’s pyplot module. Here is the code with inline comments explaining how to plot using Matplotlib’s .scatter():

可以使用Matplotlib的pyplot模块创建图形。这是带有内联注释的代码，解释了如何使用Matplotlib的.scatter()进行绘制：

# Create a scatter plot
plt.scatter(x, y, alpha=0.4)# Create x-axis label and y-axis label
plt.xlabel("the x-axis label")
plt.ylabel("the y-axis label")# Create a title
plt.title("title!")# Show the plot
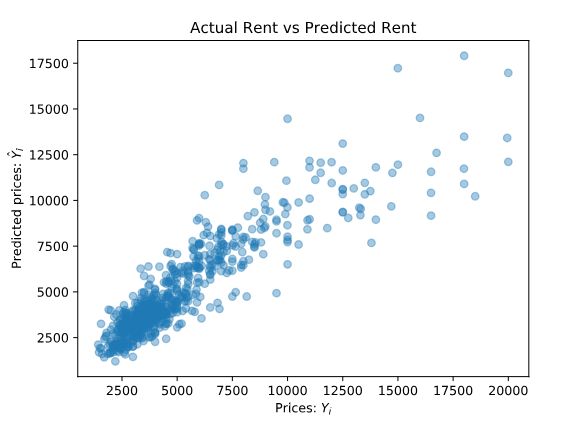
plt.show()

We want to create a scatterplot like this:

我们想要创建一个散点图，如下所示：

多元线性回归方程 (Multiple Linear Regression Equation)

Now that we have implemented Multiple Linear Regression, we will learn how to tune and evaluate the model. Before we do that, however, it’s essential to learn the equation behind it.

现在，我们已经实现了多元线性回归，我们将学习如何调整和评估模型。但是，在执行此操作之前，必须了解其背后的等式。

Equation 1 The equation for multiple linear regression that uses two independent variables is this:

公式1使用两个自变量的多元线性回归公式为：

y = b + m_{1}x_{1} + m_{2}x_{2}y=b+m1x1+m2x2

Equation 2 The equation for multiple linear regression that uses three independent variables is this:

公式2使用三个自变量的多重线性回归公式如下：

y = b + m_{1}x_{1} + m_{2}x_{2} + m_{3}x_{3}y=b+m1x1+m2x2+m3x3

Equation 3 As a result, since multiple linear regression can use any number of independent variables, its general equation becomes:

公式3结果是，由于多元线性回归可以使用任意数量的自变量，因此其一般公式为：

y = b + m_{1}x_{1} + m_{2}x_{2} + ... + m_{n}x_{n}y=b+m1x1+m2x2+...+mnxn

Here, m1, m2, m3, … mn refer to the coefficients, and b refers to the intercept that you want to find. You can plug these values back into the equation to compute the predicted y values.

在这里， m1 ， m2 ， m3 ，… mn是系数， b是您要查找的截距。您可以将这些值重新插入方程式以计算预测的y值。

Remember, with sklearn‘s LinearRegression() method, we can get these values with ease.

记住，使用sklearn的LinearRegression()方法，我们可以轻松获得这些值。

The .fit() method gives the model two variables that are useful to us:

.fit()方法为模型提供了两个对我们有用的变量：

.coef_, which contains the coefficients
.coef_ ，其中包含系数
.intercept_, which contains the intercept
.intercept_ ，其中包含拦截

After performing multiple linear regression, you can print the coefficients using .coef_.

执行多次线性回归后，您可以使用.coef_打印系数。

Coefficients are most helpful in determining which independent variable carries more weight. For example, a coefficient of -1.345 will impact the rent more than a coefficient of 0.238, with the former impacting prices negatively and latter positively.

系数最有助于确定哪个自变量具有更大的权重。例如，系数-1.345对租金的影响大于系数0.238，前者对价格产生负面影响，而后者对价格产生正面影响。

解释图 (Interpreting graphs)

In regression, the independent variables will either have a positive linear relationship to the dependent variable, a negative linear relationship, or no relationship. A negative linear relationship means that as X values increase, Y values will decrease. Similarly, a positive linear relationship means that as X values increase, Y values will also increase.

在回归中，自变量将与因变量具有正线性关系，为负线性关系或无关系。负线性关系表示随着X值增加，Y值将减小。类似地，正线性关系意味着随着X值增加，Y值也将增加。

Graphically, when you see a downward trend, it means a negative linear relationship exists. When you find an upward trend, it indicates a positive linear relationship. Here are two graphs indicating positive and negative linear relationships:

从图形上看，当您看到下降趋势时，表明存在负线性关系。当您发现上升趋势时，它表示正线性关系。这是两个图表，分别显示正线性关系和负线性关系：

评估模型的准确性 (Evaluating the Model’s Accuracy)

When trying to evaluate the accuracy of our multiple linear regression model, one technique we can use is Residual Analysis.

尝试评估多元线性回归模型的准确性时，可以使用的一种技术是残差分析 。

The difference between the actual value y, and the predicted value ŷ is the residual e. The equation is:

实际值y与预测值difference之差为残差e 。等式是：

e = y - \hat{y}e=y−y^

In the StreetEasy dataset, y is the actual rent and the ŷ is the predicted rent. The real y values should be pretty close to these predicted y values.

在StreetEasy数据集，Y是实际房租和Y是预测的租金。实际y值应非常接近这些预测的y值。

sklearn‘s linear_model.LinearRegression comes with a .score() method that returns the coefficient of determination R² of the prediction.

sklearn的linear_model.LinearRegression带有.score()方法，该方法返回预测的确定系数R²。

The coefficient R² is defined as:

系数R²定义为：

1 - \frac{u}{v}1−vuwhere u is the residual sum of squares:((y - y_predict) ** 2).sum()

and v is the total sum of squares (TSS):

v是平方和(TSS)：

((y - y.mean()) ** 2).sum()

The TSS tells you how much variation there is in the y variable.

TSS告诉您y变量有多少变化。

R² is the percentage variation in y explained by all the x variables together.

R²是y的百分比变化，由所有x变量共同解释。

For example, say we are trying to predict rent based on the size_sqft and the bedrooms in the apartment and the R² for our model is 0.72 — that means that all the x variables (square feet and number of bedrooms) together explain 72% variation in y (rent).

例如，假设我们正在尝试根据size_sqft和公寓中的bedrooms来预测rent ，而我们的模型的R²为size_sqft这意味着所有x变量(平方英尺和卧室数)共同解释了72％的变化y( rent )。

Now let’s say we add another x variable, building’s age, to our model. By adding this third relevant x variable, the R² is expected to go up. Let say the new R² is 0.95. This means that square feet, number of bedrooms and age of the building together explain 95% of the variation in the rent.

现在假设我们在模型中添加了另一个x变量，即建筑的年龄。通过添加第三个相关的x变量，R²有望上升。假设新的R²为0.95。这意味着平方英尺，卧室数量和建筑物的年龄共同解释了租金变化的95％。

The best possible R² is 1.00 (and it can be negative because the model can be arbitrarily worse). Usually, a R² of 0.70 is considered good.

最佳可能的R²为1.00(并且可以为负，因为模型可能会更差)。通常，R²为0.70被认为是良好的。

重建模型 (Rebuild the Model)

Now let’s rebuild the model using the new features as well as evaluate the new model to see if we improved!

现在，让我们使用新功能重建模型，并评估新模型以查看是否有所改进！

For Manhattan, the scores returned:

对于Manhattan ，得分返回：

Train score: 0.772546055982
Test score:  0.805037197536

For Brooklyn, the scores returned:

对于Brooklyn ，得分返回：

Train score: 0.613221453798
Test score:  0.584349923873

For Queens, the scores returned:

对于Queens ，得分返回：

Train score: 0.665836031009
Test score:  0.665170319781

评论 (Review)

Great work! Let’s review the concepts before you move on:

做得好！在继续之前，让我们回顾一下这些概念：

Multiple Linear Regression uses two or more variables to make predictions about another variable:
多元线性回归使用两个或多个变量对另一个变量进行预测：

y = b + m_{1}x_{1} + m_{2}x_{2} + ... + m_{n}x_{n}y=b+m1x1+m2x2+...+mnxn

Multiple linear regression uses a set of independent variables and a dependent variable. It uses these variables to learn how to find optimal parameters. It takes a labeled dataset and learns from it. Once we confirm that it’s learned correctly, we can then use it to make predictions by plugging in new x values.
多元线性回归使用一组自变量和一个因变量。它使用这些变量来学习如何找到最佳参数。它需要一个标记的数据集并从中学习。确认正确学习后，我们便可以使用它通过插入新的x值进行预测。
We can use scikit-learn’s LinearRegression() to perform multiple linear regression.
我们可以使用scikit-learn的 LinearRegression()进行多元线性回归。
Residual Analysis is used to evaluate the regression model’s accuracy. In other words, it’s used to see if the model has learned the coefficients correctly.
残差分析用于评估回归模型的准确性。换句话说，它用于查看模型是否正确学习了系数。
Scikit-learn’s linear_model.LinearRegression comes with a .score() method that returns the coefficient of determination R² of the prediction. The best score is 1.0.
Scikit-learn的linear_model.LinearRegression带有.score()方法，该方法返回预测的确定系数R²。最高分是1.0。

翻译自: https://medium.com/swlh/multiple-linear-regression-in-machine-learning-451367352e52