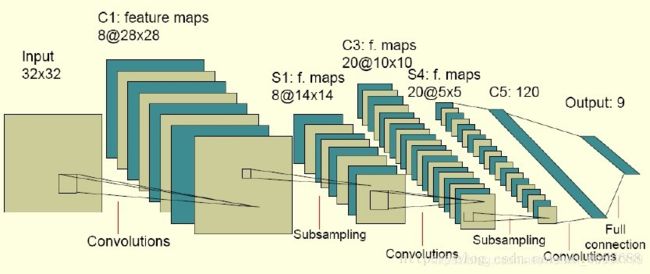
深度学习——卷积神经网络CNN学习

卷积神经网络

一、卷积神经网络与BP网络（传统前馈神经网络）相比具有以下特点：

（1）、采取局部连接（稀疏连接），减少了所需参数；
（2）、可直接处理二维数据，故常被用于图片处理操作；
（3）、具有三个基本层——卷积层、池化层、全连接层：

1. 卷积层

   CNN算法常用于图片处理，其中卷积层是通过多个卷积核对输入的图片像素矩阵进行局部连接，通过权值共享与卷积的方式进行图片的特征提取得到特征映射数据。（所以卷积核又可以看作是特征提取器或者过滤器）
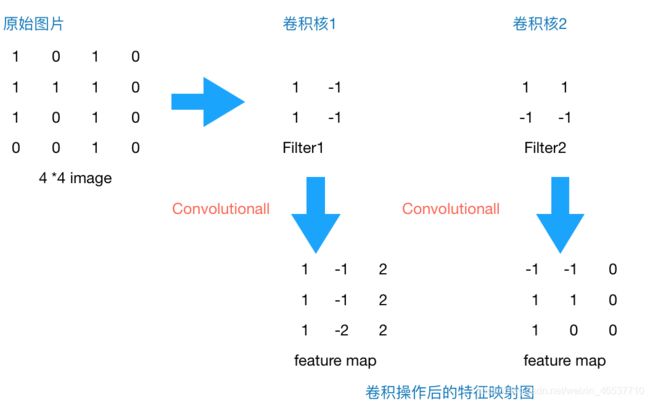
   由上图可知，卷积操作后的特征映射图（feature_map）的尺寸计算公式为——[(input_size-filter_size)/stride]+1.(input_size——原图片尺寸，filter_size——卷积核尺寸，stride——步长，即卷积核卷积一次后移动的距离，这里卷积核尺寸为正方形）
   卷积运算并非矩阵乘法运算，而是卷积核与图片连接部位对应相同位置数字相乘，在经过多次步长移动后，各部位所得数字相加求和所得。
   通过学习所知，一般情况下，越靠近输入层的卷积层设定少量的卷积核，越往后卷积层设定的卷积核数越多。

所获与思考：
a、对于卷积核尺寸，卷积核不一定是正方形。卷积核若为矩形时，feature_map的尺寸则应对长、宽分别进行计算，具体公式可借鉴正方形的卷积核。

b、步长在一般情况下默认为向侧移动与向下移动距离相同，即stride_w=stride_h=stride.

2. 池化层
   池化层是在卷积操作后图片通过激活函数所得特征映射图之后对图片进行的进一步操作，池化层在保持原有图片特征不变的情况下，通过降采样（子抽样）的方式对图片进行压缩，以此来减少参数。
   池化方法一般有以下两种：
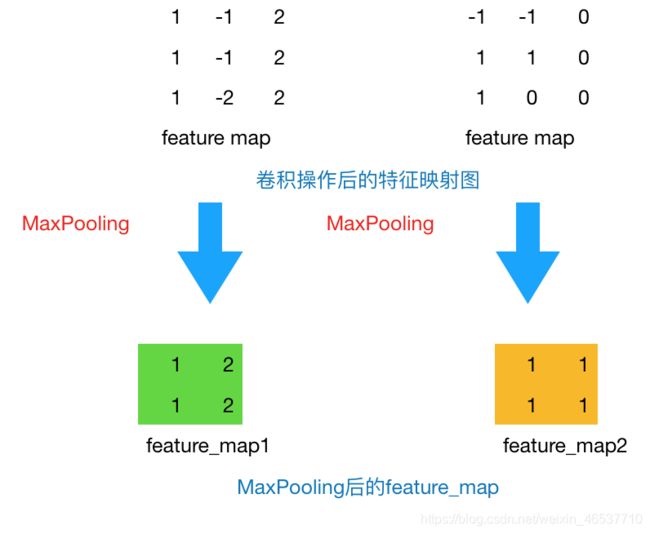
   【1】MaxPooling:取滑动窗口里最大的值
   【2】AveragePooling:取滑动窗口内所有值的平均值
   

为防止图片经过卷积层与池化层后尺寸过小，经常会使用Zero Padding（补零）操作。补零后feature_map_size=(input_size+2*padding_size-filter_size)/stride+1.（padding_size为补零宽度）

3. 全连接层
   在图片进行完最后一次卷积层和池化层之后，将所得新图形数据以一维形式总形排列（即变为单列），最终进行全连接，得到输出层。

二、公式推导

1. 前向传播
   （1）输入层到卷积层
   假设步长stride为1，如图
   
   O11=activator（i11h11+i12h12+i21h21+i22h22+bia1）
   （activator——激活函数，其他神经元输出计算方式类似）

（2）卷积层到池化层

池化层假设采用MaxPooling方式进行压缩，该层无激活函数。
m11=max（O11，O12，O21，O22）

（3）池化层到全连接层：该过程只是将数据排列形式转换成单列，无任何计算操作。

（4）全连接层到输出层：通过softmax函数进行分类计算后输出，得到不同类别的概率值，从而分辨图片类别。

3. 反向传播
   由BP算法中反向传播方法可知：
   a、反向传播计算每个神经元的误差项δi,j=∂E/∂Ii,j(卷积后feature_map的第一个神经元输入为I1,1，E表示预期输出值与实际输出值的平方差的一半）;
   b、计算每个神经元权重wi,j的梯度，Δwi,j=-n∂E/∂wi,j=-∂E/∂Ii,j∂Ii,j/∂wi,j;
   c、权重更新wi,j=wi,j+Δwi,j(n表示学习率）

CNN算法中
（1）卷积层反向传播
设net11为i11上一层神经元的输出值，因为上一级神经元输出值等于下一级的输入值，所以i11=activator（net11）， i11*h11+i12*h12+i21*h21+i22*h22=net’11，则

δ11=∂E/∂net11=∂E/∂i11*∂i11/∂net11

其中,第一项：
∂E/∂i11=∂E/∂net’11∂net’11/∂i11=δ11h11
（因为 i11h11+i12h12+i21h21+i22h22=net’11，所以∂net11/∂i11=h11）
通过上式以此类推，可得：
∂E/∂i12=∂E/∂net’11∂net’11/∂i12+∂E/∂net’12∂net’12/∂i12=δ11h12+δ12h11，（i12参与了net’11与net’12的运算，以下同理）
∂E/∂i13=δ12h12+δ13h11，
∂E/∂i21=δ11h21+δ21h11，
···
由上可整理得到，∂E/∂ii,j等于δi,j矩阵在补零后与ii,j达到相同大小后与翻转乐180°的卷积核的乘积，即 ∂E/∂ii,j=Σm*Σn h(m,n)*δ(i+m,j+n)

第二项：
因为i11=activator（net11）=f(net11)，所以
∂i11/∂net11=f’(net11)

所以δi,j=Σm*Σn h(m,n)*δ(i+m,j+n)*f’(neti,j)

由上述有wi,j=hi,j,(以h11为例）
∂E/∂h11=∂E/∂net’11∂net’11/h11+···+∂E/∂net’33∂net’33/∂h11
=δ11h11+···+δ33h11;(net’i,j为所有h11参与到的卷积运算所得项）

所以Δwi,j=-n*∂E/∂hi,j=-n*ΣmΣn δ(m,n)*O(i+m,j+n)

而bia的梯度，Δbias= n*∂E/∂b=∂E/∂net’11∂net’11/∂b+∂E/∂net’12∂net’12/∂b+···+∂E/∂net’33∂net’33/∂b
因为∂net’ij/∂b=1，所以
∂E/∂b=n*ΣiΣj δi,j
所以
bias=bias+Δbias。

（2）池化层反向传播
有前馈传播可知
m11=max(O11,O12,O21,O22)，所以
∂m11/∂O11=1（假设O11最大），
∂m11/∂O12=∂m11/∂O21=∂m11/∂O22=0，
所以
δ11(l-1)=∂E/∂O11=∂E/∂m11*∂m11/∂O11=δ11(l)
δ12(l-1)=δ21(l-1)=δ22(l-1)=0
同卷积层可求各神经元的权重与偏倚更新公式。

三、算法实现(待更新）

1. 构造激活函数sigmoid

class Sigmoid(object):
    def forward(self,w_input):
        return 1.0/(1.0+np.exp(-w_input))
    def backward(self,output):
        return output*(1-output)

Reference:
【1】【深度学习系列】卷积神经网络CNN原理详解（一）、（二）
https://www.cnblogs.com/charlotte77/p/7759802.html
https://www.cnblogs.com/charlotte77/p/7783261.html

【2】Deep Learning模型之：CNN卷积神经网络（一）深度解析CNN
https://blog.csdn.net/u010555688/article/details/24487301