recording:59.螺旋矩阵II

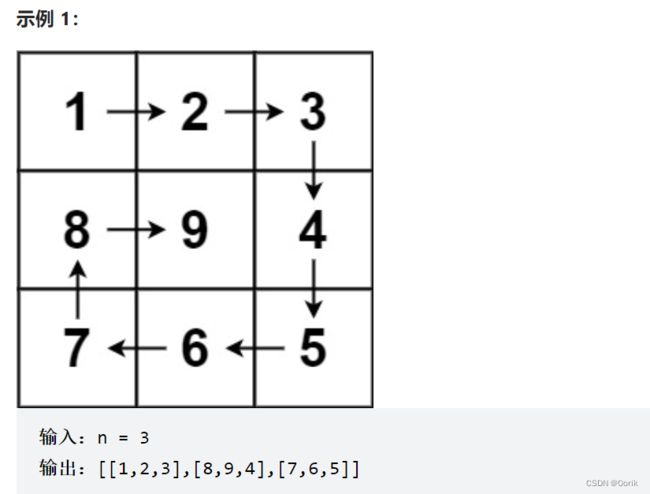
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

这种题没有什么算法，就是模拟整个过程，注意循环模拟时的边界，这里我用左闭右开的写法，意思就是在模拟第一行的时候最后一个数不填，模拟列的时候把这个数字当做第一个数，填进去，同时此列的最后一个数也不填，放在下一次去填入

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

这里每一种颜色，代表一条边，我们遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。

这也是坚持了每条边左闭右开的原则。

class Solution {
public:
    vector> generateMatrix(int n) {
        
        vector> vv (n,vector (n,0));
        int startx=0;//起始x下标
        int starty=0;//起始y下标
        int count=1;//用来赋值用的 1->2->3->4...
        int offset=1;//每个拐点保证第一次不赋值,左闭右开
        int lose=n/2;//要模拟几圈
        int mid=n/2;//如果n是奇数，最后[mid][mid]赋值用
        int i,j;//下标
        while(lose>0)//开始一圈一圈模拟
        {
            i=startx;
            j=starty;
            //从左往右开始模拟
            for(j;jstarty;--j)
            {
                vv[i][j]=count++;
            }
            //从下往上模拟
            for(i;i>startx;--i)
            {
                vv[i][j]=count++;
            }
            //第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;
            //一圈模拟完该下一圈模拟
            lose--;
            //offset 控制每一圈里每一条边遍历的长度,拐点的位置发生了变化
            offset+=1;
        }
        //如果n是奇数要填充中心
        if(n%2)
        {
            vv[mid][mid]=count;
        }
        //返回矩阵
        return vv;
}
};

力扣题解里面找到了一个大佬用一种类似循环队列，循环坐标的思路写的，非常牛逼,膜拜大佬学不来，具体思路说难不难，但是一般人想不到

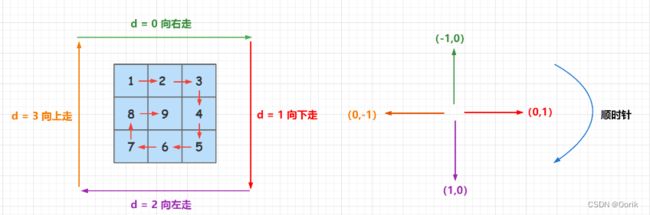
1、我们顺时针定义四个方向：上右下左。d = 0表示向右走，d = 1 表示向下走，d = 2表示向左走，d = 3表示向上走，方向偏移数组定义为 dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0}，如下图所示：

2、当前位置定义为(x,y)，使用 d = (d + 1) % 4来更改方向，那么下个要走的位置(a, b)则表示为： a = x + dx[d], b = y + dy[d]。

3、从左上角开始遍历，先往右走，走到不能走为止，然后更改到下个方向，再走到不能走为止，依次类推，遍历 n^2个格子后停止。

时间复杂度分析： 矩阵中的每个数都被遍历一次，因此时间复杂度为O(n^2)O(n^2)，nn是给定的正整数。 

就是这个大佬，感兴趣的可以去力扣看他的题解，说的很清晰了，下面就贴一下大佬的代码 

class Solution {
public:
    vector> generateMatrix(int n) {
        vector>res(n, vector(n, 0));
        int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};  //方向偏移数组
        int x = 0, y = 0;  //当前位置
        for(int i = 1, d = 0; i <= n*n; i++)
        {
            res[x][y] = i; 
            int a = x + dx[d], b = y + dy[d]; 
            if(a <0 || a == n || b < 0 || b == n || res[a][b]){  //出界或者该位置已经被走过
                d = (d + 1) % 4;   //更改方向
                a = x + dx[d], b = y + dy[d];  //下一个要走的位置
            }
            x = a, y = b;    
        }
        return res;
    }
};