初步认识机器学习(Machine Leaning)
一.概述
1.人工智能>机器学习>深度学习|强化学习
2.机器学习(ML:machine leaning):一门通过优化方法(线性回归、逻辑回归、决策树、向量机、贝叶斯模型等)挖掘数据中规律的学科。
3.机器学习:输入==>函数==>输出,现在已知输入输出数据,由机器学习拟合出一个比较好的函数来符合输入输出
4.机器学习的本质是统计模型训练,其主要工作是训练模型,也可以叫做拟合模型,即拟合数据是机器学习的主要工作,总结一个字就是“猜”
5.机器学习过程(类似猜数字游戏):算法模型输出一个数值,损失函数经过计算,回馈一个偏差结果,算法模型根据这个偏差结果进行调整,再输出一个数值,周而复始,直到正确为止。
6.假设函数(Hypothesis Function):给假设函数灌入数据作为“燃料”,它就能产生动力输出并让学习过程运转起来
7.损失函数(Loss Function):为机器学习提供学习动力,将假设函数的预测结果与实际进行对比得到偏差数值
8.机器学习的基本模式
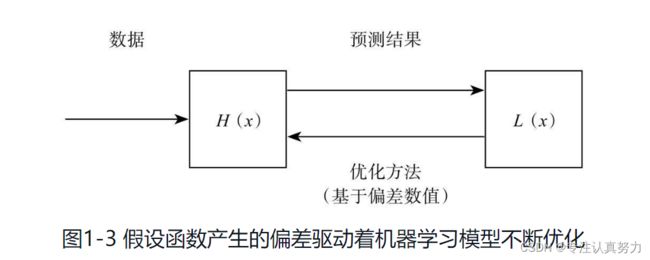
9.优化方法可以基于偏差数值对假设函数的参数进行调整,以使其逼近拟合
10.机器学习问题分类
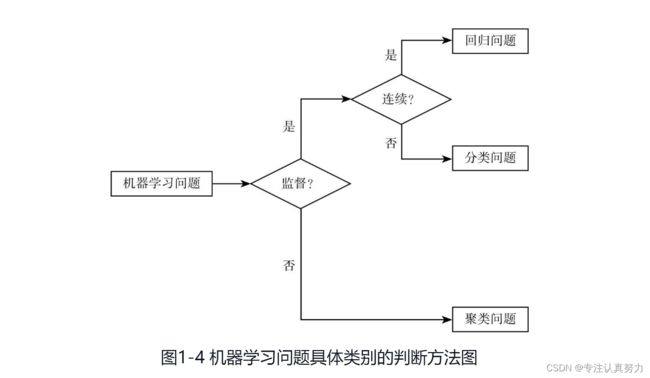
11.有监督学习:可以理解为有参考答案的学习,具体来说,就是数据集中包含了预测结果
12.常用的机器学习算法
1.线性回归算法:最简单的机器学习算法,用线性方法解决回归问题
2.Logistic回归分类算法:是线性回归算法的“孪生兄弟”,其核心思想仍然是线性方法,具有解决分类问题的能力
3.KNN分类算法:不依赖数学或统计模型,纯粹依靠“生活经验”的算法,它通过“找最近邻”的思想解决分类问题
4.朴素贝叶斯分类算法:认为结果不是确定性的而是概率性的,解决的是分类问题
5.决策树分类算法:类似于if-else的逻辑进行分类
6.支持向量机分类算法:将线性不可分的数据点映射成线性可分,再用最简单的线性方法来解决问题
7.K-means聚类算法
8.神经网络分类算法
二.环境
1.机器学习三件套
支持库Numpy:专门设计用于科学计算的专业支持库
算法库Scikit-Learn:机器学习算法库
数据处理库Pandas:内置许多排序、统计之类的实用功能
2.Numpy
命令行安装
pip install -U numpy
pip下载过慢:可以把 -i https://pypi.douban.com/simple 作为必填的末尾内容
导入
import numpy as np
3.Scikit-Learn
命令行安装
pip install -U scikit-learn -i https://pypi.douban.com/simple
导入
import sklearn
4.Pandas
命令行安装
pip install -U pandas -i https://pypi.douban.com/simple
导入
import pandas as pd
三.线性回归算法(Linear Regression)
1.使用线性模型解决回归问题
2.回归问题:拟合历史连续数据,预测未来连续数据
3.在错误中学习:偏差度量+权值调整
4.假设函数的数学表达式
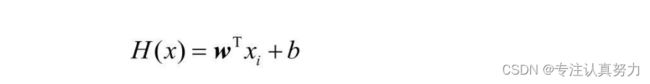
5.损失函数的数学表达式
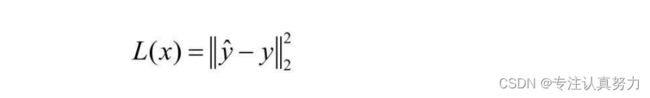
6.优化方法的数学表达式

7.线性回归算法信息表

8.线性回归问题的三步

9.在Python中使用线性回归算法
import matplotlib.pyplot as plt # 二维画图
import numpy as np # 科学计算库
from sklearn import linear_model # 机器学习算法库
# 生成数据集
x = np.linspace(-3, 3, 30)
y = 2 * x + 1
# 添加扰动
x = x + np.random.rand(30)
y = y + np.random.rand(30)
# 数据集转换:序列==>矩阵
x.shape = len(x), -1
y.shape = len(y), -1
# 训练线性回归模型
model = linear_model.LinearRegression()
model.fit(x, y)
# 测试输入
x_ = [[1], [2]]
# 预测输出
y_ = model.predict(x_)
print(y_)
# 法向量w和截距b
w = model.coef_
b = model.intercept_
print(w, b)
# 数据集绘图
y2 = w[0][0] * x + b[0] # 拟合直线
plt.scatter(x, y)
plt.plot(x, y2)
plt.show()
四.Logistic回归分类算法(Logistic Regression)
1.分类问题:与回归问题相比,它的预测值是离散的而非连续的,二元分类是多元分类的基础
2.Logistic函数:可导的跃迁函数,自变量以0为界,左趋近于0,右趋近于1
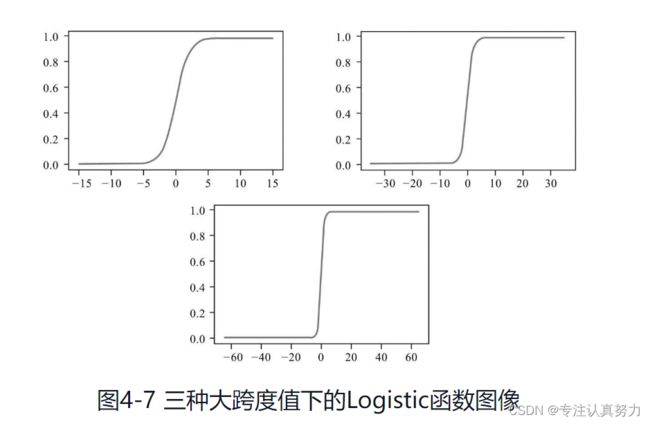
通过Logistic函数,可以将连续的值映射为跃迁的离散值,所以它是联系连续和离散的桥梁
Logistic函数的数学表达式如下:
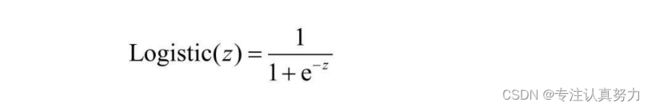
使用Logistic回归解决分类问题的核心思路:
一是使用线性方程勾画直线。
二是通过Logistic函数把直线“掰弯”,从而拟合呈离散分布的分类问题数据点,相当于首先通过Logistic函数把分类问题映射成回归问题,然后使用可以解决回归问题的线性模型来解决分类问题。
3.使用Logistic函数映射连续值为离散值的思路

4.机器学习中的分类类别形式

5.Logistic回归的假设函数
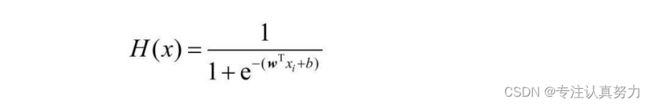
6.Logistic回归的损失函数
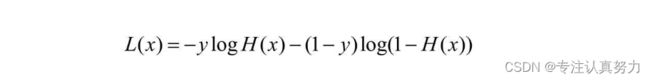
7.Logistic回归分类算法信息表

8.Logistic回归分类算法步骤

9.在Python中使用Logistic回归算法
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris # 导入鸢尾花分类数据集
X, y = load_iris(return_X_y=True) # 载入鸢尾花数据集
clf = LogisticRegression(max_iter=1000).fit(X, y) # 训练模型
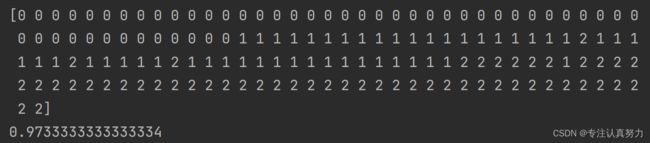
y_ = clf.predict(X) # 使用模型进行分类预测
print(y_) # 分类结果
print(clf.score(X, y)) # 性能评估
五.KNN分类算法(K-Nearest Neighbor)
1.算法原则
同类相吸:对于新输入的待分类样本究竟该归为哪一堆的问题,也就转化成新样本和哪一堆的样本共同点最多、最为相像。与哪一堆像,新样本就归为哪一堆,即分成哪一类。
多数表决:根据它各个维度的值,看看与它临近的点都是什么类,按多数表决原则,哪些类占大多数,这个新样本就属于哪一类
邻近表决:以待分类点为圆心,就可以找到与它临近的点有哪些,从而构成它的“朋友圈”。只有在圈子里的点才拥有对于这个点属于哪个类的表决权,而不是由全体样本进行表决
2.以待分类样本点为中心,距离最近的K个点。这K个点中什么类别的占比最多,待分类样本点就属于什么类别。
3.如何确定最近邻个数K?
需要根据实际情况调节以便取得更好拟合效果的参数,可以根据交叉验证等实验方法,结合工作经验进行设置,一般情况下,K的值会在3~10之间
4.如何确定最近邻?
关键是使用什么方法度量“最近”,这是KNN以及相关衍生算法需要解决的首要问题,是难点,也是创新点
可以利用闵可夫斯基距离(Minkowski Distance)来进行度量
5.KNN算法分类过程

6.闵可夫斯基距离
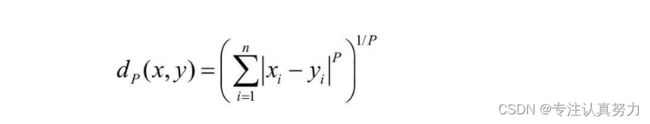
当P=1时:

当P=2时:
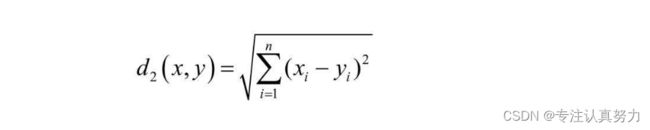
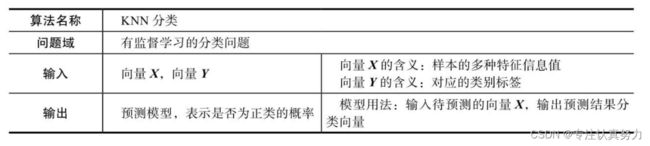
7.KNN分类算法信息表
8.KNN分类算法实现步骤

9.在Python中使用KNN分类算法
from sklearn.datasets import load_iris # 从Scikit-Learn库导入近邻模型中的KNN分类算法
from sklearn.neighbors import KNeighborsClassifier # 载入鸢尾花数据集
X, y = load_iris(return_X_y=True) # 训练模型
clf = KNeighborsClassifier().fit(X, y) # 使用模型进行分类预测
y_ = clf.predict(X)
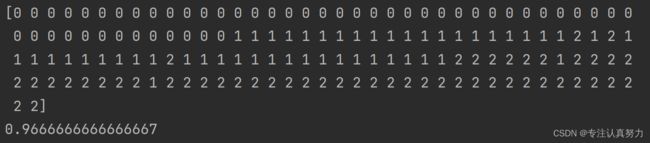
print(y_) # 预测分类结果
print(clf.score(X, y)) # 算法性能评估
六.朴素贝叶斯分类算法(Naive Bayes)
1.朴素贝叶斯分类算法的核心是贝叶斯公式,贝叶斯公式的核心是条件概率
2.朴素贝叶斯:在“朴素”假设条件下运用“贝叶斯公式”
3.概率与条件概率

4.条件概率实质是量化了X与Y的相关性
5.逻辑性与相关性的区别:逻辑性是因果关系,相关性是建立在统计数据的基础之上
6.贝叶斯公式预测的核心思想就5个字——“看起来更像”
7.贝叶斯公式希望利用已知经验来进行判断。用“经验”进行“判断”,经验怎么来?有了经验怎么判断?一句话实际包含了两轮过程。

8.先验概率、后验概率和可能性函数

即先验概率通过可能性函数的修正可以得到后验概率
若A发生的概率为先验概率,在发生了一件会影响A发生概率的B发生后,此时A发生的概率称为后验概率
9.类别的后验概率与特征的似然度

类别的后验概率

某个特征的似然度表示

10.朴素贝叶斯分类算法的数学解析
“朴素”的假设:特征与特征之间是相互独立、互不影响的(这个假设是为了解决数据采集总是有缺失和不全,所以特征x越多,这两个问题就会越突出,要统计这些特征同时出现的概率就越困难)
于是某个特征的似然度就可以简化为:

后验概率正比于似然度
朴素贝叶斯算法利用后验概率进行预测,核心方法是通过似然度预测后验概率,而学习的过程就是不断提高似然度的过程。
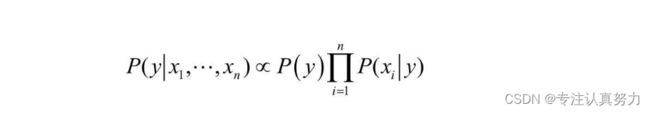
如果采用等式,就仍然需要统计特征共同出现的概率:
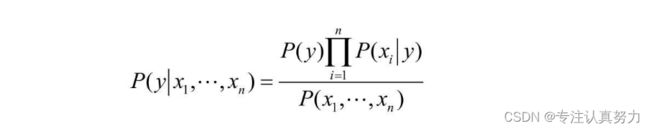
朴素贝叶斯的优化方法:
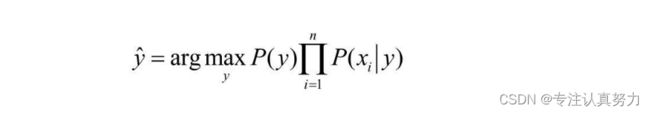
11.朴素贝叶斯分类算法信息表

12.朴素贝叶斯分类算法的实现步骤

13.在Python中使用朴素贝叶斯分类算法
from sklearn.datasets import load_iris # 从Scikit-Learn库导入朴素贝叶斯模型中的多项式朴素贝叶斯分类算法
from sklearn.naive_bayes import MultinomialNB # 载入鸢尾花数据集
X, y = load_iris(return_X_y=True) # 训练模型
clf = MultinomialNB().fit(X, y) # 使用模型进行分类预测
y_ = clf.predict(X)
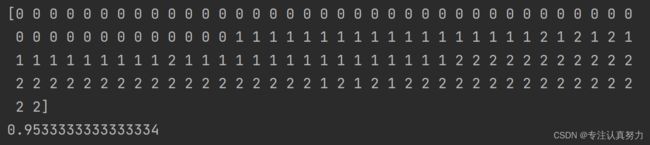
print(y_)
print(clf.score(X, y))
七.决策树分类算法(Decision Tree)
1.程序员观点:if-else层层相套
2.如何选择判断条件来生成判断分支是决策树算法的核心要点
3.决策树的判别条件是从这个特征维度集里产生的
4.怎样才算是好的决策条件:最理想的情况当然是选好决策条件后,一个if-else就正好把数据集按正类和负类分成两个部分。退而求其次,希望分类结果中这些不识时务的杂质越少越好,也就是分类结果越纯越好。
5.节点纯度的度量规则

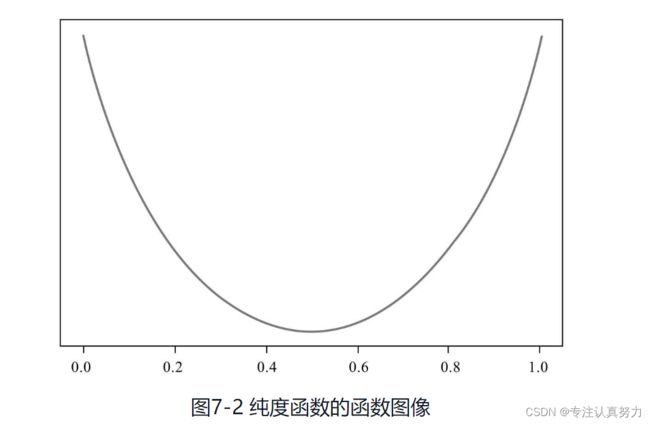
6.决策树的剪枝问题
现实是可能由于各种原因,如数据集收集片面或随机扰动等,导致数据出现了假性关联,那么这些实际无效的属性维度就会被决策树算法当作有效的分支判断条件。用这种存在假性关联数据集训练得到的决策树模型就会出现过度学习的情况,学到了并不具备普遍意义的分类决策条件,也就是出现过拟合,导致决策树模型的分类有效性降低。
根据剪枝操作触发时机的不同,基本可以分成两种,一种称为预剪枝,另一种称为后剪枝
无论预剪枝还是后剪枝,剪枝都分为剪枝判断和剪枝操作两个步骤,只有判断为需要剪枝的,才会实际进行剪枝操作
7.决策树分类算法的基本思路
判别条件从何而来?
这个问题分为两个步骤解决。第一步是来源,数据集中的数据都是以特征维度进行组织的,这些特征维度也可以作为一个集合,称为帖子维度集,或者称为属性集。我们要发现特征维度与类别可能存在的关联关系,所以判别条件就从这个集合中来。
选取哪一个特征维度作为当前if-else的判别条件呢?
这就需要进行比较,要比较就需要有标准,所以我们引入了“纯度”的概念,哪个特征维度“提纯”效果最好,就选哪个特征维度作为判别条件。
决策树该在什么时候停止节点分裂呢?

决策树分类算法的一个核心就是在数据的特征集中依次选择决策条件,也就是完成if-else判断分支的分裂。
如何度量不同特征条件下分类结果的纯度,是决策树分类算法的核心问题。
8.决策树分类算法信息表

9.决策树分类算法实现步骤

10.在Python中使用决策树分类算法
from sklearn.datasets import load_iris # 从Scikit-Learn库导入决策树模型中的决策树分类算法
from sklearn.tree import DecisionTreeClassifier # 载入鸢尾花数据集
X, y = load_iris(return_X_y=True) # 训练模型
clf = DecisionTreeClassifier().fit(X, y) # 使用模型进行分类预测
y_ = clf.predict(X)
print(y_)
print(clf.score(X, y))
八.支持向量机分类算法(Support Vector Machine)
1.间隔:不同类之间的距离,线性可分问题可以利用间距中的一条直线进行分类,对于线性不可分问题,需要先进行高维映射处理
2.支持向量:处于间隔边缘的数据点称为支持向量,它们对正确分类非常重要
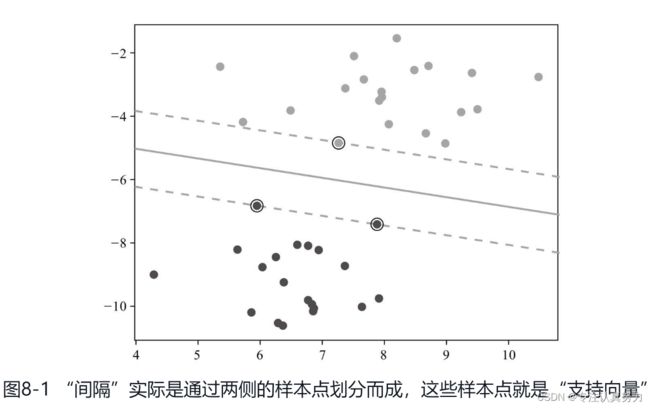
3.高维映射:低维的线性不可分映射到高维后可以具有可分性
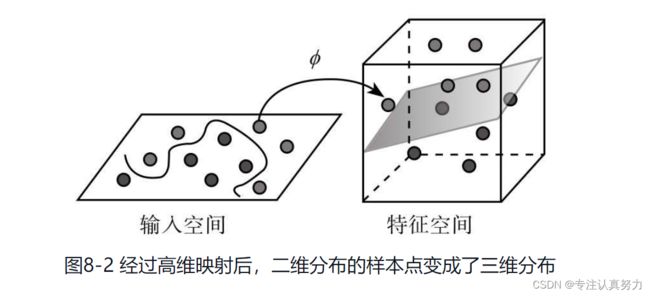
4.核函数:在支持向量机中完成高维映射这种功能的函数

5.算法分类步骤

6.算法信息表

7.在Python中使用支持向量机分类算法
from sklearn.datasets import load_iris # 从Scikit-Learn库导入支持向量机算法
from sklearn.svm import SVC # 载入鸢尾花数据集
X, y = load_iris(return_X_y=True) # 训练模型
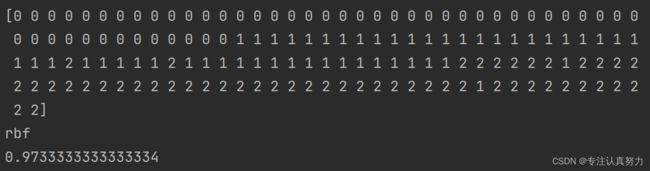
clf = SVC().fit(X, y) # 默认为径向基rbf,可通过kernel查看
print(clf.predict(X))
print(clf.kernel)
print(clf.score(X, y))
九.K-means聚类算法
1.聚类问题最基本的原则:找相似
2.相同点多了就是同一类,不同点多了就不是同一类
3.簇:样本数据集通过聚类算法最终会聚成一个个“类”,这些类在机器学习的中文术语里就称为“簇
4.聚类过程就可以看成是不断寻找簇的质心的过程,这个过程从随机设定K个质心开始,直到找到K个真正质心为止。
5.聚类最终将产生多少个不同的簇可以预先设定为K,即按K个类别将数据进行分类
6.质心:在数据集中随机选取K个点作为质心,以它们为中心进行聚类,可以用均值来调整质心,从而让随机选取的K个质心也能最终达到我们所期望的目标。
7.多数表决:K-means算法表决的是聚类问题,是“咱们是不是同一个簇”,即大家都是待判别,并没有任何一个样本数据点可以作为中心点,所以需要选取一些点作为质心
8.找质心过程的本质:让簇内样本点到达各自质心的距离的总和最小。能够满足这个“最小”的K个质心,就是我们要找的质心。
9.算法信息表和实现步骤

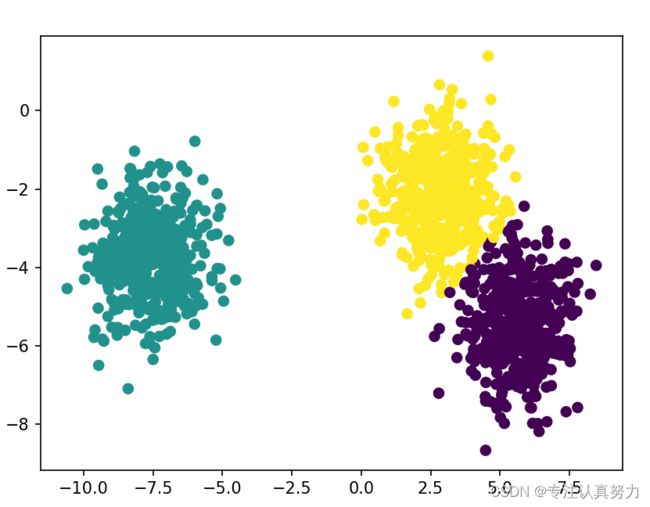
10.在Python中使用K-means聚类算法
# 导入绘图库
import matplotlib.pyplot as plt
# #从Scikit-Learn库导入聚类模型中的K-means聚类算法
from sklearn.cluster import KMeans
# #导入聚类数据生成工具
from sklearn.datasets import make_blobs
# 用sklearn自带的make_blobs方法生成聚类测试数据
n_samples = 1500
# #该聚类数据集共1500个样本
X, y = make_blobs(n_samples=n_samples)
# #进行聚类,这里n_clusters设定为3,也即聚成3个簇
y_pred = KMeans(n_clusters=3).fit_predict(X)
# #用点状图显示聚类效果
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
十.神经网络分类算法(Artificial Neural Network, ANN)
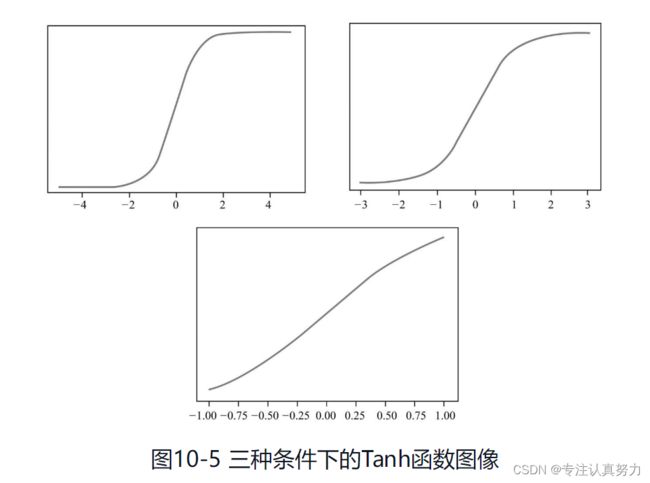
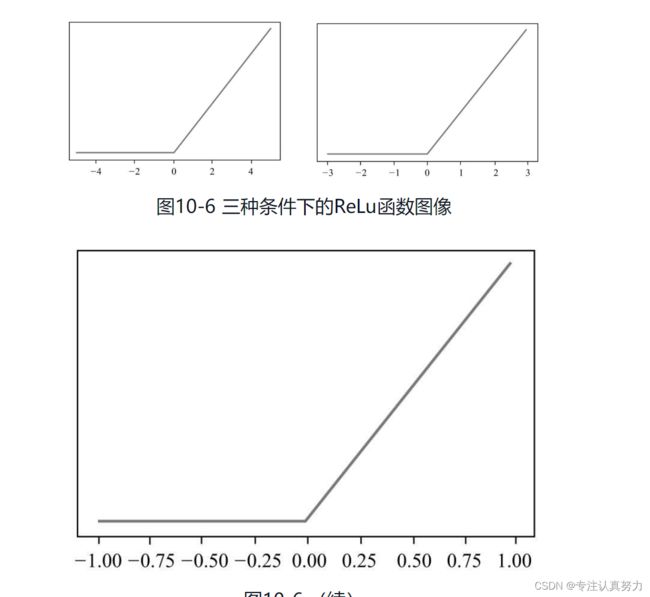
1.神经网络算法有“三宝”,神经元、激活函数和反向传播机制。
2.神经元


3.兴奋传递
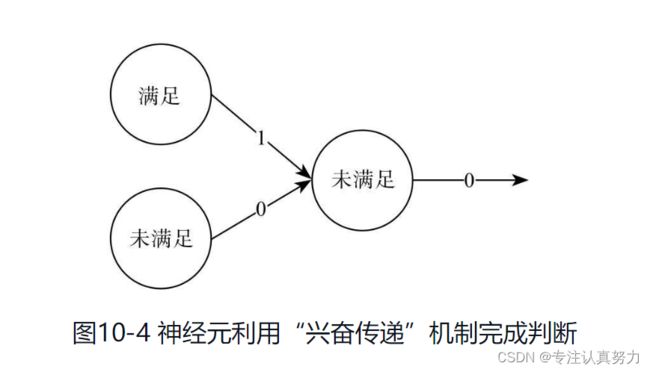
5.反向传播机制
6.神经元的核心工作机制就是根据刺激来决定是否激活,激活就继续往前传导刺激,否则刺激就在此中断,不会对最终的输出产生影响
7.神经网络结构