【动手学深度学习v2】学习笔记02:线性代数、矩阵计算、自动求导
前文回顾:数据操作、数据预处理
文章目录
- 一、线性代数实现
-
- 1.1 标量和向量
- 1.2 矩阵和多维张量
- 1.3 张量的运算
-
- 1.3.1 基础运算
- 1.3.2 按特定轴运算
- 1.3.3 乘积运算
- 1.3.4 范数
- 二、矩阵计算
-
- 2.1 标量导数
- 2.2 向量导数
-
- 2.2.1 标量-向量求导
- 2.2.2 向量-标量求导
- 2.2.3 向量-向量求导
- 三、自动求导
-
- 3.1 链式法则
- 3.2 自动求导
- 3.3 计算图
- 3.4 两种模式
-
- 3.4.1 正向累积与反向累积
- 3.4.2 反向累积步骤
- 3.4.3 复杂度
- 四、自动求导实现
-
- 4.1 常用函数
- 4.2 简易流程
- 4.3 进一步
一、线性代数实现
1.1 标量和向量
在pytorch中,我们使用一个元素的张量来表示标量。
我们可以将向量视为标量值组成的列表。
x = torch.tensor([3.0]) # 标量
y = torch.tensor([2.0, 1.0, 4.0]) # 向量
1.2 矩阵和多维张量
我们可以通过制定两个分量m和n来创建一个形状为 m × n m \times n m×n的矩阵。并且,通过T运算,我们可以对矩阵进行转置。
A = torch.arange(20).reshape(4, 5) # 矩阵
AT = A.T # 转置
对称矩阵B,等于其转置: B = B τ B = B^\tau B=Bτ
就像向量是标量的推广,矩阵是向量的推广一样,我们可以构建具有更多轴的数据结构。
X = torch.arange(24).reshape(2, 3, 4) # 三维张量
上例中X的内容为:
[ [ 0 1 2 3 4 5 6 7 8 9 10 11 ] [ 12 13 14 15 16 17 18 19 20 21 22 23 ] ] \begin{bmatrix} \begin{bmatrix} 0 & 1 & 2 & 3 \\ 4 & 5 & 6 & 7 \\ 8 & 9 & 10 & 11 \end{bmatrix} \begin{bmatrix} 12 & 13 & 14 & 15 \\ 16 & 17 & 18 & 19 \\ 20 & 21 & 22 & 23 \end{bmatrix} \end{bmatrix} ⎣ ⎡⎣ ⎡04815926103711⎦ ⎤⎣ ⎡121620131721141822151923⎦ ⎤⎦ ⎤
1.3 张量的运算
给定任意两个具有相同形状的张量,任何按元素二元运算的结果都将是相同形状的向量。
1.3.1 基础运算
加减乘除:下例中,A、B和C三个矩阵的形状相同。
A = torch.arange(20, dtype=torch.float32).reshape(4, 5)
B = A.clone() # 通过重新分配内存,将A的一个副本分配给B
C = A + B
哈达玛积:两个矩阵的按元素乘法称为哈达玛积(数学符号 ⨀ \bigodot ⨀)
A = torch.arange(20, dtype=torch.float32).reshape(4, 5)
B = A.clone()
C = A * B # 哈达玛积
上例和视为如下运算:
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] ⨀ [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] = [ 0. 1. 4. 9. 16. 25. 36. 49. 64. 81. 100. 121. 144. 169. 196. 225. 256. 289. 324. 361. ] \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} \bigodot \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} = \begin{bmatrix} 0. & 1. & 4. & 9. \\ 16. & 25. & 36. & 49. \\ 64. & 81. & 100. & 121. \\ 144. & 169. & 196. & 225. \\ 256. & 289. & 324. & 361. \end{bmatrix} ⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤⨀⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤=⎣ ⎡0.16.64.144.256.1.25.81.169.289.4.36.100.196.324.9.49.121.225.361.⎦ ⎤
与标量的运算
a = 2
X = torch.arange(24).reshape(2, 3, 4)
Y = a + X
1.3.2 按特定轴运算
| 运算 | 方法 | 保持维度不变 |
|---|---|---|
| 按特定轴求和 | sum(axis=n) |
sum(axis=n, keepdims=True) |
| 按特定轴求均值 | mean(axis=n) |
mean(axis=n, keepdims=True) |
| 按特定轴累加 | cumsum(axis=n) |
cumsum(axis=n, keepdims=True) |
按特定轴求和:我们可以使用sum()方法,计算其所有元素的和。也可以通过指定axis参数来对张量的部分维度求和。
A = torch.arange(40, dtype=torch.float32).reshape(2, 5, 4)
A_sum_axis0 = A.sum(axis=0)
上例中,我们创建了一个形状为 2 × 5 × 4 2\times5\times4 2×5×4的三维张量A,并通过sum(axis=0)方法对其第一维度进行求和。
[ [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] [ 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. ] ] ⟶ [ 20. 22. 24. 26. 28. 30. 32. 34. 36. 38. 40. 42. 44. 46. 48. 50. 52. 54. 56. 58. ] \begin{bmatrix} \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} \begin{bmatrix} 20. & 21. & 22. & 23. \\ 24. & 25. & 26. & 27. \\ 28. & 29. & 30. & 31. \\ 32. & 33. & 34. & 35. \\ 36. & 37. & 38. & 39. \end{bmatrix} \end{bmatrix} \longrightarrow \begin{bmatrix} 20. & 22. & 24. & 26. \\ 28. & 30. & 32. & 34. \\ 36. & 38. & 40. & 42. \\ 44. & 46. & 48. & 50. \\ 52. & 54. & 56. & 58. \end{bmatrix} ⎣ ⎡⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤⎣ ⎡20.24.28.32.36.21.25.29.33.37.22.26.30.34.38.23.27.31.35.39.⎦ ⎤⎦ ⎤⟶⎣ ⎡20.28.36.44.52.22.30.38.46.54.24.32.40.48.56.26.34.42.50.58.⎦ ⎤
同理,我们也可以按照其他的维度进行按维度求和。
相似地,我们可以按特定轴求均值。
A = torch.arange(40, dtype=torch.float32).reshape(2, 5, 4)
A_ave_axis0 = A.mean(axis=0)
按特定轴累加求和:下例是按第1维度累加求和
A.cumsum(axis=1)
[ [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] [ 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. ] ] ⟶ [ [ 0. 1. 2. 3. 4. 6. 8. 10. 12. 15. 18. 21. 24. 28. 32. 36. 40. 45. 50. 55. ] [ 20. 21. 22. 23. 44. 46. 48. 50. 72. 75. 78. 81. 104. 108. 112. 116. 140. 145. 150. 155. ] ] \begin{bmatrix} \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} \begin{bmatrix} 20. & 21. & 22. & 23. \\ 24. & 25. & 26. & 27. \\ 28. & 29. & 30. & 31. \\ 32. & 33. & 34. & 35. \\ 36. & 37. & 38. & 39. \end{bmatrix} \end{bmatrix} \longrightarrow \begin{bmatrix} \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 6. & 8. & 10. \\ 12. & 15. & 18. & 21. \\ 24. & 28. & 32. & 36. \\ 40. & 45. & 50. & 55. \end{bmatrix} \begin{bmatrix} 20. & 21. & 22. & 23. \\ 44. & 46. & 48. & 50. \\ 72. & 75. & 78. & 81. \\ 104. & 108. & 112. & 116. \\ 140. & 145. & 150. & 155. \end{bmatrix} \end{bmatrix} ⎣ ⎡⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤⎣ ⎡20.24.28.32.36.21.25.29.33.37.22.26.30.34.38.23.27.31.35.39.⎦ ⎤⎦ ⎤⟶⎣ ⎡⎣ ⎡0.4.12.24.40.1.6.15.28.45.2.8.18.32.50.3.10.21.36.55.⎦ ⎤⎣ ⎡20.44.72.104.140.21.46.75.108.145.22.48.78.112.150.23.50.81.116.155.⎦ ⎤⎦ ⎤
保持维度不变:我们可以通过指定keepdims参数,在计算总和或均值时保持轴数(维度)不变。这样做的好处是,我们可以保持原张量的维度,便于利用广播机制——因为广播机制只能作用于维度相同的两个张量。
A = torch.arange(40, dtype=torch.float32).reshape(2, 5, 4)
sum_A = A.sum(axis=1, keepdims=True)
上例对矩阵A的第1维度进行按轴求和,并保持轴数不变,这样做实际上是将第1维度的大小设置为1。
[ [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] [ 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. ] ] ⟶ [ [ [ 40. 45. 50. 55. ] [ 140. 145. 150. 155. ] ] ] \begin{bmatrix} \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} \begin{bmatrix} 20. & 21. & 22. & 23. \\ 24. & 25. & 26. & 27. \\ 28. & 29. & 30. & 31. \\ 32. & 33. & 34. & 35. \\ 36. & 37. & 38. & 39. \end{bmatrix} \end{bmatrix} \longrightarrow \begin{bmatrix} \begin{bmatrix} \begin{bmatrix} 40. & 45. & 50. & 55. \end{bmatrix} \begin{bmatrix} 140. & 145. & 150. & 155. \end{bmatrix} \end{bmatrix} \end{bmatrix} ⎣ ⎡⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤⎣ ⎡20.24.28.32.36.21.25.29.33.37.22.26.30.34.38.23.27.31.35.39.⎦ ⎤⎦ ⎤⟶[[[40.45.50.55.][140.145.150.155.]]]
1.3.3 乘积运算
| 乘积 | 方法 |
|---|---|
| 向量向量点积 | dot(x, y) |
| 矩阵向量积 | mv(A, x) |
| 矩阵矩阵乘法 | mm(A, B) |
点积:相同位置的按元素乘积的和。
X = torch.arange(4, dtype=torch.float32)
Y = torch.ones(4, dtype=torch.float32)
Z = torch.dot(X, Y)
上例可视为如下运算:
[ 0. 1. 2. 3. ] ⋅ [ 1. 1. 1. 1. ] = 0 × 1 + 1 × 1 + 2 × 1 + 3 × 1 = 6 \begin{bmatrix} 0. & 1. & 2. & 3. \end{bmatrix} \cdot \begin{bmatrix} 1. & 1. & 1. & 1. \end{bmatrix} = 0\times1+1\times1+2\times1+3\times1 =6 [0.1.2.3.]⋅[1.1.1.1.]=0×1+1×1+2×1+3×1=6
此外,我们还可以通过执行按元素乘法,然后进行求和来表示两个向量的点积:torch.sum(X * Y)。
矩阵向量积 A x ⃗ A\vec{x} Ax:是一个长度为m的列向量,其 i t h i^{th} ith元素是点积 a ⃗ i τ x \vec{a}_i^\tau x aiτx
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
X = torch.arange(4, dtype=torch.float32)
torch.mv(A, X)
上例可视为如下运算:
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] [ 0. 1. 2. 3. ] = [ 14. 38. 62. 86. 110. ] \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} \begin{bmatrix} 0. \\ 1. \\ 2. \\ 3. \end{bmatrix} = \begin{bmatrix} 14. \\ 38. \\ 62. \\ 86. \\ 110. \end{bmatrix} ⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤⎣ ⎡0.1.2.3.⎦ ⎤=⎣ ⎡14.38.62.86.110.⎦ ⎤
矩阵矩阵乘法:
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.ones(4, 3)
torch.mm(A, B)
上例可看成如下运算:
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. ] [ 1 1 1 1 1 1 1 1 1 1 1 1 ] = [ 6. 6. 6. 22. 22. 22. 38. 38. 38. 54. 54. 54. 70. 70. 70. ] \begin{bmatrix} 0. & 1. & 2. & 3. \\ 4. & 5. & 6. & 7. \\ 8. & 9. & 10. & 11. \\ 12. & 13. & 14. & 15. \\ 16. & 17. & 18. & 19. \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 6. & 6. & 6. \\ 22. & 22. & 22. \\ 38. & 38. & 38. \\ 54. & 54. & 54. \\ 70. & 70. & 70. \end{bmatrix} ⎣ ⎡0.4.8.12.16.1.5.9.13.17.2.6.10.14.18.3.7.11.15.19.⎦ ⎤⎣ ⎡111111111111⎦ ⎤=⎣ ⎡6.22.38.54.70.6.22.38.54.70.6.22.38.54.70.⎦ ⎤
1.3.4 范数
| 范数 | 方法 |
|---|---|
| L 1 L_1 L1范数 | abs(向量).sum() |
| L 2 L_2 L2范数 | norm(向量) |
| F范数 | norm(矩阵) |
L 1 L_1 L1范数:它表示为向量元素的绝对值之和:
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||x||_1=\sum_{i=1}^{n} |x_i| ∣∣x∣∣1=i=1∑n∣xi∣
u = torch.tensor([3.0, -4.0])
v = torch.abs(u).sum()
L 2 L_2 L2范数:是向量元素平方和的平方根:
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 n x i 2 ||x||_2=\sqrt{\sum_{i=1}^{n} x_i^2} ∣∣x∣∣2=i=1∑nxi2
u = torch.tensor([3.0, -4.0])
v = torch.norm(u)
F范数:是矩阵元素的平方和的平方根:
∣ ∣ x ∣ ∣ F = ∑ i = 1 m ∑ j = 1 n x i j 2 ||x||_F=\sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} x_{ij}^2} ∣∣x∣∣F=i=1∑mj=1∑nxij2
vf = torch.norm(torch.ones((4, 9)))
二、矩阵计算
2.1 标量导数
| y y y | a a a(常数) | x n x^n xn | e x e^x ex | ln x \ln{x} lnx | sin x \sin{x} sinx |
|---|---|---|---|---|---|
| d y d x \frac{dy}{dx} dxdy | 0 0 0 | n x n − 1 nx^{n-1} nxn−1 | e x e^x ex | 1 x \frac{1}{x} x1 | cos x \cos{x} cosx |
| y y y | u + v u+v u+v | u v uv uv | y = f ( u ) , u = g ( x ) y=f(u),u=g(x) y=f(u),u=g(x) |
|---|---|---|---|
| d y d x \frac{dy}{dx} dxdy | d u d x + d v d x \frac{du}{dx}+\frac{dv}{dx} dxdu+dxdv | d u d x v + d v d x u \frac{du}{dx}v+\frac{dv}{dx}u dxduv+dxdvu | d y d u d u d x \frac{dy}{du}\frac{du}{dx} dudydxdu |
2.2 向量导数
| 类别 | x x x | x ⃗ \vec{x} x |
|---|---|---|
| y y y | ∂ y ∂ x \frac{\partial y}{\partial x} ∂x∂y(标量) | ∂ y ∂ x ⃗ \frac{\partial y}{\partial \vec{x}} ∂x∂y(向量) |
| y ⃗ \vec{y} y | ∂ y ⃗ ∂ x \frac{\partial \vec{y}}{\partial x} ∂x∂y(向量) | ∂ y ⃗ ∂ x ⃗ \frac{\partial \vec{y}}{\partial \vec{x}} ∂x∂y(矩阵) |
2.2.1 标量-向量求导
这种情况实际上是标量对向量中的每一个元素分别求偏导,再将结果组合成一个行向量。
x ⃗ = [ x 1 x 2 ⋮ x n ] ∂ y ∂ x ⃗ = [ ∂ y ∂ x 1 ∂ y ∂ x 2 ⋯ ∂ y ∂ x n ] \vec{x}= \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \qquad \qquad \frac{\partial y}{\partial \vec{x}}= \begin{bmatrix} \frac{\partial y}{\partial x_1} & \frac{\partial y}{\partial x_2} & \cdots & \frac{\partial y}{\partial x_n} \end{bmatrix} x=⎣ ⎡x1x2⋮xn⎦ ⎤∂x∂y=[∂x1∂y∂x2∂y⋯∂xn∂y]
常见的导数如下所示:
| y y y | a a a(常数) | a u au au | s u m ( x ) sum(x) sum(x) | ∣ ∣ x ∣ ∣ 2 \mid \mid x\mid \mid ^2 ∣∣x∣∣2 |
|---|---|---|---|---|
| ∂ y ∂ x ⃗ \frac{\partial y}{\partial \vec{x}} ∂x∂y | 0 ⃗ T \vec{0}^T 0T | a ∂ u ∂ x ⃗ a\frac{\partial u}{\partial \vec{x}} a∂x∂u | 1 ⃗ T \vec{1}^T 1T | 2 x ⃗ T 2\vec{x}^T 2xT |
| y y y | u + v u+v u+v | u v uv uv | ⟨ u ⃗ , v ⃗ ⟩ \langle \vec{u}, \vec{v} \rangle ⟨u,v⟩ |
|---|---|---|---|
| ∂ u ∂ x ⃗ \frac{\partial u}{\partial \vec{x}} ∂x∂u | ∂ u ∂ x ⃗ + ∂ v ∂ x ⃗ \frac{\partial u}{\partial \vec{x}}+\frac{\partial v}{\partial \vec{x}} ∂x∂u+∂x∂v | ∂ u ∂ x ⃗ v + ∂ v ∂ x ⃗ u \frac{\partial u}{\partial \vec{x}}v+\frac{\partial v}{\partial \vec{x}}u ∂x∂uv+∂x∂vu | u ⃗ T ∂ v ⃗ ∂ x ⃗ + v ⃗ T ∂ u ⃗ ∂ x ⃗ \vec{u}^T\frac{\partial \vec{v}}{\partial \vec{x}}+\vec{v}^T\frac{\partial \vec{u}}{\partial \vec{x}} uT∂x∂v+vT∂x∂u |
2.2.2 向量-标量求导
这种情况相当于向量的每一个元素分别求导。
y ⃗ = [ y 1 y 2 ⋮ y m ] ∂ y ⃗ ∂ x = [ ∂ y 1 ∂ x ∂ y 2 ∂ x ⋮ ∂ y m ∂ x ] \vec{y}= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix} \qquad \qquad \frac{\partial \vec{y}}{\partial x}= \begin{bmatrix} \frac{\partial y_1}{\partial x} \\ \frac{\partial y_2}{\partial x} \\ \vdots \\ \frac{\partial y_m}{\partial x} \end{bmatrix} y=⎣ ⎡y1y2⋮ym⎦ ⎤∂x∂y=⎣ ⎡∂x∂y1∂x∂y2⋮∂x∂ym⎦ ⎤
我们发现 ∂ y ∂ x ⃗ \frac{\partial y}{\partial \vec{x}} ∂x∂y是行向量,而 ∂ y ⃗ ∂ x \frac{\partial \vec{y}}{\partial x} ∂x∂y是列向量。这个被称之为分子布局符号,反过来的版本叫分母布局符号。
2.2.3 向量-向量求导
这种情况相当于分别进行前述两种求导。
x = [ x 1 x 2 ⋮ x n ] y = [ y 1 y 2 ⋮ y m ] ∂ y ⃗ ∂ x ⃗ = [ ∂ y 1 ∂ x ⃗ ∂ y 2 ∂ x ⃗ ⋮ ∂ y m ∂ x ⃗ ] = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ⋯ ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ⋯ ∂ y 2 ∂ x n ⋮ ⋮ ⋮ ∂ y m ∂ x 1 ∂ y m ∂ x 2 ⋯ ∂ y m ∂ x n ] x= \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \qquad y= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix} \qquad \frac{\partial \vec{y}}{\partial \vec{x}}= \begin{bmatrix} \frac{\partial y_1}{\partial \vec{x}} \\ \frac{\partial y_2}{\partial \vec{x}} \\ \vdots \\ \frac{\partial y_m}{\partial \vec{x}} \end{bmatrix}= \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n} \\ \end{bmatrix} x=⎣ ⎡x1x2⋮xn⎦ ⎤y=⎣ ⎡y1y2⋮ym⎦ ⎤∂x∂y=⎣ ⎡∂x∂y1∂x∂y2⋮∂x∂ym⎦ ⎤=⎣ ⎡∂x1∂y1∂x1∂y2⋮∂x1∂ym∂x2∂y1∂x2∂y2⋮∂x2∂ym⋯⋯⋯∂xn∂y1∂xn∂y2⋮∂xn∂ym⎦ ⎤
常见的导数如下所示:
| y ⃗ \vec{y} y | a ⃗ \vec{a} a(常数) | x ⃗ \vec{x} x | A x ⃗ A\vec{x} Ax | x ⃗ T A \vec{x}^TA xTA |
|---|---|---|---|---|
| ∂ y ⃗ ∂ x ⃗ \frac{\partial \vec{y}}{\partial \vec{x}} ∂x∂y | 0 ⃗ \vec{0} 0 | I I I(单位矩阵) | A A A | A T A^T AT |
| y ⃗ \vec{y} y | a u ⃗ a\vec{u} au | A u ⃗ A\vec{u} Au | u ⃗ + v ⃗ \vec{u}+\vec{v} u+v |
|---|---|---|---|
| ∂ y ⃗ ∂ x ⃗ \frac{\partial \vec{y}}{\partial \vec{x}} ∂x∂y | a ∂ u ⃗ ∂ x ⃗ a\frac{\partial \vec{u}}{\partial \vec{x}} a∂x∂u | A ∂ u ⃗ ∂ x ⃗ A\frac{\partial \vec{u}}{\partial \vec{x}} A∂x∂u | ∂ u ⃗ ∂ x ⃗ + ∂ v ⃗ ∂ x ⃗ \frac{\partial \vec{u}}{\partial \vec{x}}+\frac{\partial \vec{v}}{\partial \vec{x}} ∂x∂u+∂x∂v |
除本文中提到的求导,张量间的求导还可以进一步往矩阵扩展,甚至向更高维度扩展。
三、自动求导
3.1 链式法则
我们可以通过求导的链式法则,实现对复杂函数导数的求解。
例:
假设 X ∈ R m × n X \in R^{m \times n} X∈Rm×n, w ⃗ ∈ R n \vec{w} \in R^n w∈Rn, y ⃗ ∈ R m \vec{y} \in R^m y∈Rm, z = ∣ ∣ X w ⃗ − y ⃗ ∣ ∣ 2 z=||X\vec{w}-\vec{y}||^2 z=∣∣Xw−y∣∣2
计算 ∂ z ∂ w ⃗ \frac{\partial z}{\partial \vec{w}} ∂w∂z
分解 a ⃗ = X w ⃗ \vec{a}=X\vec{w} a=Xw, b ⃗ = a ⃗ − y ⃗ \vec{b}=\vec{a}-\vec{y} b=a−y, z = ∣ ∣ b ⃗ ∣ ∣ 2 z=||\vec{b}||^2 z=∣∣b∣∣2
求导
∂ z ∂ w ⃗ = ∂ z ∂ b ⃗ ∂ b ⃗ ∂ a ⃗ ∂ a ⃗ ∂ w ⃗ = ∂ ∣ ∣ b ⃗ ∣ ∣ 2 ∂ b ⃗ ∂ a ⃗ − y ⃗ ∂ a ⃗ ∂ X w ⃗ ∂ w ⃗ = 2 b ⃗ T × I × X = 2 ( X w ⃗ − y ⃗ ) T X \frac{\partial z}{\partial \vec{w}}= \frac{\partial z}{\partial \vec{b}}\frac{\partial \vec{b}}{\partial \vec{a}}\frac{\partial \vec{a}}{\partial \vec{w}}=\frac{\partial ||\vec{b}||^2}{\partial \vec{b}}\frac{\partial \vec{a}-\vec{y}}{\partial \vec{a}}\frac{\partial X \vec{w}}{\partial \vec{w}}=2\vec{b}^T \times I \times X=2(X \vec{w}-\vec{y})^TX ∂w∂z=∂b∂z∂a∂b∂w∂a=∂b∂∣∣b∣∣2∂a∂a−y∂w∂Xw=2bT×I×X=2(Xw−y)TX
3.2 自动求导
自动求导:计算一个函数在指定值上的导数。
它有别于
- 符号求导(显式计算)
I n [ 1 ] : = D [ 4 x 3 + x 2 + 3 , x ] O u t [ 1 ] : = 2 x + 12 x 2 In[1]: = D[4x^3+x^2+3, x] \\ Out[1]: = 2x+12x^2 In[1]:=D[4x3+x2+3,x]Out[1]:=2x+12x2 - 数学求导
∂ f ( x ) ∂ x = lim h → 0 f ( x + h ) − f ( x ) h \frac{\partial f(x)}{\partial x}=\lim \limits_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} ∂x∂f(x)=h→0limhf(x+h)−f(x)
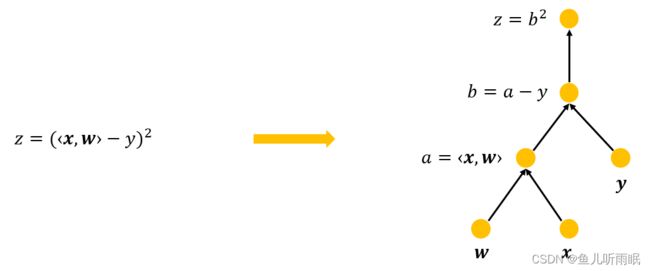
3.3 计算图
3.4 两种模式
3.4.1 正向累积与反向累积
- 链式法则: ∂ y ∂ x = ∂ y ∂ u n ∂ u n ∂ u n − 1 ⋯ ∂ u 2 ∂ u 1 ∂ u 1 ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}} \cdots \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x} ∂x∂y=∂un∂y∂un−1∂un⋯∂u1∂u2∂x∂u1
- 正向累积: ∂ y ∂ x = ∂ y ∂ u n ( ∂ u n ∂ u n − 1 ( ⋯ ( ∂ u 2 ∂ u 1 ∂ u 1 ∂ x ) ) ) \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}(\frac{\partial u_n}{\partial u_{n-1}}( \cdots (\frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}))) ∂x∂y=∂un∂y(∂un−1∂un(⋯(∂u1∂u2∂x∂u1)))
- 反向累积(反向传递): ∂ y ∂ x = ( ( ( ∂ y ∂ u n ∂ u n ∂ u n − 1 ) ⋯ ) ∂ u 2 ∂ u 1 ) ∂ u 1 ∂ x \frac{\partial y}{\partial x}=(((\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}}) \cdots )\frac{\partial u_2}{\partial u_1})\frac{\partial u_1}{\partial x} ∂x∂y=(((∂un∂y∂un−1∂un)⋯)∂u1∂u2)∂x∂u1
3.4.2 反向累积步骤
首先,构造计算图。
前向:执行图,存储中间结果。
反向:从相反方向执行图,并去除不需要的枝。

3.4.3 复杂度
- 正向累积:
- 计算复杂度:O(n),用来计算一个变量的梯度。
- 内存复杂度:O(1)
- 反向累积:
- 计算复杂度:O(n),n是操作子个数。
- 内存复杂度:O(n),因为需要存储正向的所有中间结果。
四、自动求导实现
4.1 常用函数
| 函数 | 功能 |
|---|---|
x.requires_grade_(True) |
表示需要存储梯度 |
y.backward() |
自动计算梯度 |
y.sum().backward() |
先求和再自动计算梯度 |
x.grad |
查看梯度 |
x.grad.zero_() |
梯度清零 |
y.detach() |
将与x相关的函数y转变为与x无关的常数 |
4.2 简易流程
在我们计算y关于x的梯度之前,我们需要一个地方来存储梯度。
x = torch.arange(4.0)
x.requires_grad_(True) # 表示需要存储梯度
我们也可以通过requires_grad参数来表示需要存储梯度。上下两段代码是等价的,但是要主要上面的代码中requires_grad_()方法最后还有一个_。
x = torch.arange(4.0, requires_grad=True)
现在让我们计算y。
y = torch.dot(x, x) * 2
通过调用反向传播函数来自动计算y关于x每个分量的梯度。
y.backward() # 自动求梯度
print(x.grad) # 查看梯度
接下来,我们来计算另一个函数中y关于x每个分量的梯度。
在默认情况下,PyTorch会累积梯度,我们需要清除之前的值。
我们这里使用的是zero_()方法,_的意识是“把xx写进xx”,因此x.grad.zero_()的含义为:把零写进x的梯度。
x.grad.zero_() # _表示将xx写进xx,即将zero写进x.grad
y = x.sum() # 另一个函数
y.backward()
print(x.grad)
4.3 进一步
深度学习中,我们的目的不是计算微分矩阵,而是批量中每个样本单独计算的偏导数之和。
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward() # 先求和再自动求梯度
print(x.grad)
我们还可以将一些计算移动到记录的计算图之外。
其中,我们用detach()方法将与x相关的函数转变为与x无关的常数,这个技巧可以用来固定网络中的参数。
x.grad.zero_()
y = x * x
u = y.detach() # 将u转变为与x无关的常数
z = u * x
z.sum().backward() # 先求和,再求梯度
print(x.grad, x.grad==u)
即使构建函数的计算图需要通过Python控制流(例如,条件、循环或者任意函数调用),我们仍然可以计算得到的变量的梯度。
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
# size = () 意为:a为标量
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
print(a.grad, a.grad==d/a)