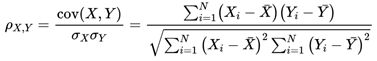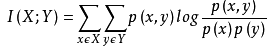机器学习特征选择方法介绍及python实现
机器学习特征选择方法介绍及python实现
- 综述
- 一、过滤法
-
- 1. 方差选择法
- 2. 相关系数法
- 3. 互信息熵法
- 4. F检验
- 二、包裹法
-
- 递归式特征消除(RFE)
- 三、嵌入法
-
- 1. 基于惩罚项的特征选择法
- 2. 基于树模型和GBDT的特征选择法
- 四、降维
-
- 1. PCA
- 2. LDA
- 总结
综述
- 当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说，从两个方面考虑来选择特征：
- 特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
- 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。
- 根据特征选择的形式又可以将特征选择方法分为3种：
- Filter（过滤法）：按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
- Wrapper（包装法）：根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
- Embedded（嵌入法）：先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，通过训练来确定特征的优劣。
一、过滤法
- 过滤法就是按照发散性或者相关性对各个特征进行评分，设定阈值或者选择阈值的个数，完成特征选择。
1. 方差选择法
- 方差选择是特征选择的一个简单基本方法，它会移除所有那些方差不满足阈值的特征。默认情况下，它将会移除所有的零方差特征，即那些在所有的样本上的取值均不变的特征。这种方法简单高效的过滤了一些低方差的特征，但是存在一个问题就是阈值的设定是一个先验条件，当设置过低时，保留了过多低效的特征，设置过高则丢弃了过多有用的特征。使用方差选择法，先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。
- 使用python sklearn包实现如下：
from sklearn.feature_selection import VarianceThreshold
"""
var:方差
data:特征数组
filter_data:返回特征数组
"""
filter_data = VarianceThreshold(threshold=var).fit_transform(data)
2. 相关系数法
- 使用相关系数法，先要计算各个特征对目标值的相关系数以及相关系数的P值。衡量的是变量之间的线性相关性，简单快速，但是只对线性关系敏感，非线性不适合
-皮尔逊相关系数计算如下：
- 使用python sklearn包实现如下：
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
"""
K:返回的特征数
data:特征数组
label:数据标签
filter_data:返回特征数组
"""
filter_data = SelectKBest(f_regression, k=K).fit_transform(data, label)
3. 互信息熵法
- 互信息(MutualInformation)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。经典的互信息也是评价定性自变量对定性因变量的相关性的，
- 互信息计算公式如下：
- 使用python sklearn包实现如下：
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif as MIC
"""
K:返回的特征数
data:特征数组
label:数据标签
filter_data:返回特征数组
"""
filter_data = SelectKBest(MIC, k=K).fit_transform(data, label)
4. F检验
-
我们希望选取p值小于0.05或0.01的特征，这些特征与标签时显著线性相关的。
-
使用python sklearn包实现如下：
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
"""
K:返回的特征数
data:特征数组
label:数据标签
filter_data:返回特征数组
"""
filter_data = SelectKBest(f_classif, k=K).fit_transform(data, label)
二、包裹法
- 所谓包裹法就是选定特定算法，然后再根据算法效果来选择特征集合。就是通过不断的启发式方法来搜索特征，主要分为如下两类：
- 选择一些特征，逐步增加特征保证算法模型精度是否达标。
- 删除一些特征，然后慢慢在保持算法精度的条件下，缩减特征。
递归式特征消除(RFE)
- 递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。它是一种贪婪的优化算法，旨在找到性能最佳的特征子集。
它反复创建模型，并在每次迭代时保留最佳特征或剔除最差特征，下一次迭代时，它会使用上一次建模中没有被选中的特征来构建下一个模型，直到所有特征都耗尽为止。 - 使用python sklearn包实现如下：
from sklearn.feature_selection import RFE
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.svm import SVC
"""
estimator:训练模型
K:返回的特征数
data:特征数组
label:数据标签
filter_data:返回特征数组
"""
# 用rbf核进行筛选是不可以的，SVR中不提供rbf特征选择的逻辑，对于支持向量回归可以用linear进行筛选
svc = SVC(kernel='linear')
filter_data = RFE(estimator=svc, n_features_to_select=K, step=2000).fit_transform(data_set, label)
# 使用随机森林
model = RFC(n_estimators=10, random_state=0)
filter_data = RFE(estimator=model, n_features_to_select=K, step=2000).fit_transform(data_set, label)
三、嵌入法
- 在使用嵌入法时，我们先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性。
1. 基于惩罚项的特征选择法
- 使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。
2. 基于树模型和GBDT的特征选择法
- 使用python sklearn包实现如下：
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier as RFC
"""
data:阈值
data_set:数据集
label:数据标签
filter_data:返回特征数组
"""
# GBDT作为基模型的特征选择
filter_data = SelectFromModel(GradientBoostingClassifier(), threshold=data).fit_transform(data_set, label)
# 使用随机森林
model = RFC(n_estimators=10, random_state=0)
filter_data = SelectFromModel(estimator=model, threshold=data).fit_transform(data_set, label)
四、降维
- 常用的方法有主成分分析（PCA），独立成分分析（ICA），线性判别分析（LDA）一般数据是有类别的，最好先考虑用LDA降维。也可先用小幅度的PCA降维消除噪声再用LDA降维，若训练数据没有类别优先考虑PCA。特征提取是由原始输入形成较少的新特征，它会破坏数据的分布，为了使得训练出的模型更加健壮，若不是数据量很大特征种类很多，一般不要用特征提取。
1. PCA
- 作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。PCA是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大（样本的分布最散乱）以使用较少的数据维度同时保留住较多的原数据点的特征。
优点：
- 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。
- 各主成分之间正交，可消除原始数据成分间的相互影响的因素。
- 计算方法简单，主要运算是特征值分解，易于实现。
缺点：
- 提取出的各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
- PCA会消除一些类信息，但是方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。
- 使用python sklearn包实现如下：
from sklearn.decomposition import PCA
"""
K:返回特征数
data_set:数据集
filter_data:返回特征数组
"""
# 主成分分析法，返回降维后的数据
# 参数n_components为主成分数目
filter_data = PCA(n_components=K).fit_transform(data_set)
2. LDA
- LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。
优点：
- 在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
- LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。
缺点：
- LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
- LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
- LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
- LDA可能过度拟合数据。
使用python sklearn包实现如下：
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
"""
K:返回特征数
data_set:数据集
filter_data:返回特征数组
label:数据集标签
"""
# 主成分分析法，返回降维后的数据
# 参数n_components为主成分数目
filter_data = LDA(n_components=K).fit_transform(data_set, label)
总结
- 过滤法更快速，但更粗糙。包装法和嵌入法更精确，比较适合具体到算法去调整，但计算量比较大，运行时间长。当数据量很大的时候，优先使用方差过滤和互信息法调整，再上其他特征选择方法。使用逻辑回归时，优先使用嵌入法。使用支持向量机时，优先使用包装法。